Теорема 4 (критерій Коші). Для збіжності невласного інтеграла
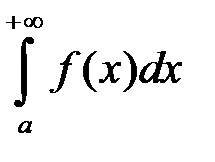 (11.1) необхідно і достатньо, щоб для будь якого
(11.1) необхідно і достатньо, щоб для будь якого 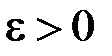 існувало таке число
існувало таке число 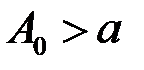 , щоб при
, щоб при 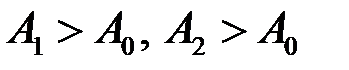 виконувалося нерівність:
виконувалося нерівність:
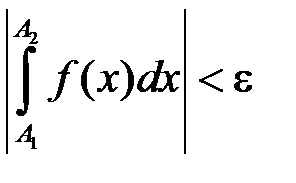 . (11.2)
. (11.2)
Доведення. Вводячи функцію 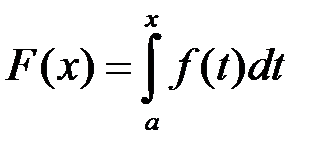 , умову теореми можна переписати так:
, умову теореми можна переписати так:
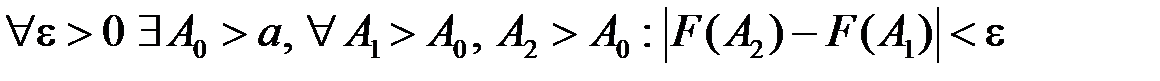 .
.
А це є критерій Коші існування скінченної границі 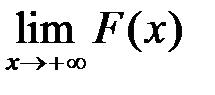 , тобто інтеграл (11.1) збігається тоді і тільки тоді, коли виконано нерівність (11.2).
, тобто інтеграл (11.1) збігається тоді і тільки тоді, коли виконано нерівність (11.2).
Аналогічні твердження справедливі для невласних інтегралів II роду.
Теорема 5. Для збіжності невласного інтеграла
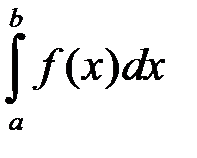 , (11.3)
, (11.3)
де 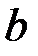 – особлива точка, необхідно і достатньо, щоб для будь якого
– особлива точка, необхідно і достатньо, щоб для будь якого 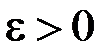 існувало
існувало 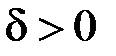 , що з нерівностей
, що з нерівностей 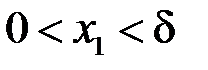 ,
, 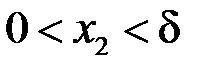 випливала нерівність
випливала нерівність
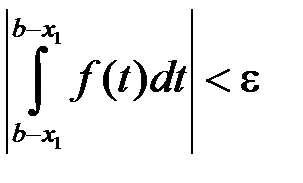 .
.
З теорем 4 та 5 випливає наступна ознака збіжності інтегралів (11.1), (11.3).
Теорема 6. Якщо збігається інтеграл 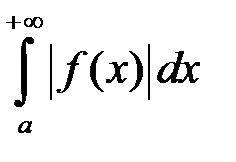 , то збігається інтег-
, то збігається інтег-
рал (11.1).
Доведення. З умови теореми на підставі теореми 4 маємо: 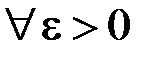
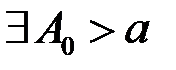 , що
, що 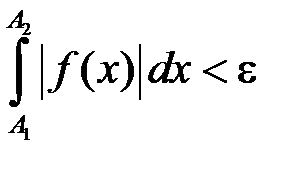 , якщо тільки
, якщо тільки 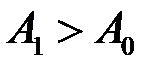 ,
, 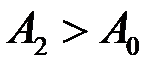 . Але
. Але
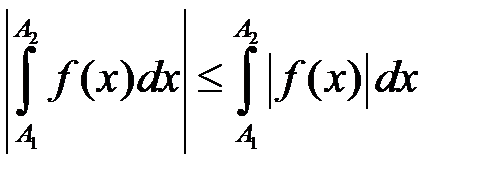 ,
,
отже для тих самих 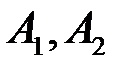 :
: 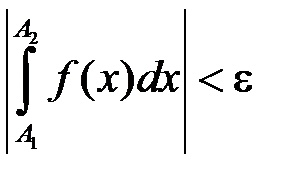 , звідки внаслідок теореми 4 випливає збіжність інтеграла (11.1).
, звідки внаслідок теореми 4 випливає збіжність інтеграла (11.1).
Теорема 7. Якщо збігається інтеграл 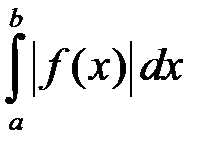 , де точка
, де точка 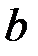 особлива, то збігається інтеграл (11.3).
особлива, то збігається інтеграл (11.3).
Зауваження. Обернені твердження до теорем 6, 7 несправедливі, а саме із збіжності інтегралів (11.1), (11.3) не випливає відповідно збіжність інтегралів 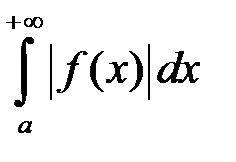 ,
, 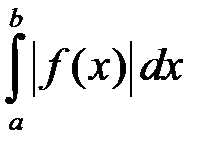 .
.
Означення. Якщо інтеграл 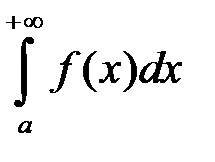 збігається, в той час, як інтеграл
збігається, в той час, як інтеграл 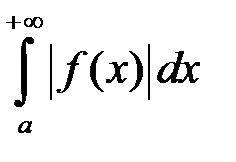 розбігається, то інтеграл
розбігається, то інтеграл 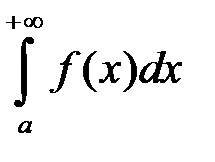 називається умовно збіжним. Якщо разом з інтегралом
називається умовно збіжним. Якщо разом з інтегралом 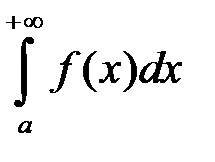 збігається і інтеграл
збігається і інтеграл 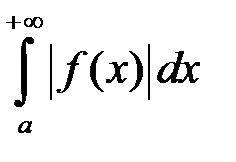 , то інтеграл
, то інтеграл 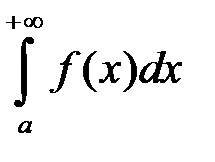 називається абсолютно збіжним.
називається абсолютно збіжним.
Аналогічні означення вводяться і для інтегралів II роду. Іншими словами, невласний інтеграл (I чи II роду) від функції 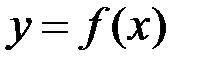 називається абсолютно збіжним, якщо збіжний інтеграл від функції
називається абсолютно збіжним, якщо збіжний інтеграл від функції 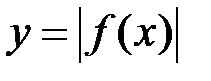 .
.
Приклади.
1. Дослідити на збіжність інтеграл
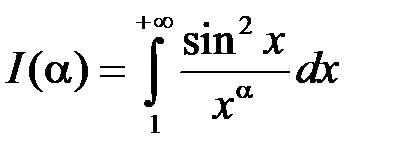 . (11.4)
. (11.4)
1) Нехай 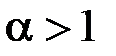 ; тоді
; тоді 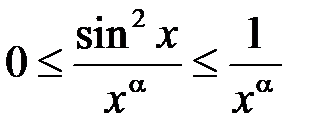 , і оскільки інтеграл
, і оскільки інтеграл 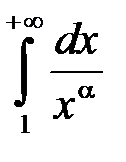 збігаєть-
збігаєть-
ся, то збіжним є й інтеграл (11.4).
2) Нехай 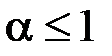 . Покажемо, що інтеграл (11.4) розбігається. Для цього
. Покажемо, що інтеграл (11.4) розбігається. Для цього
скористаємось критерієм Коші, а саме покажемо, що існує 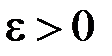 таке, що
таке, що 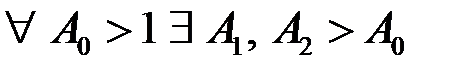 такі, що
такі, що
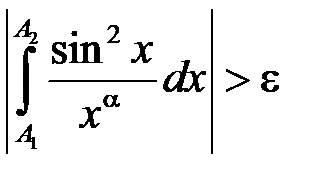 .
.
Нехай 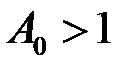 . Покладемо
. Покладемо 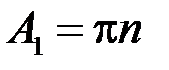 ,
, 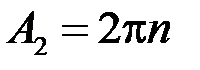 , де натуральне
, де натуральне 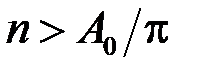 . Тоді, оскільки при
. Тоді, оскільки при 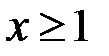 ,
, 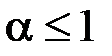 :
: 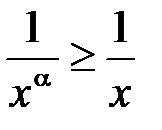 , то
, то
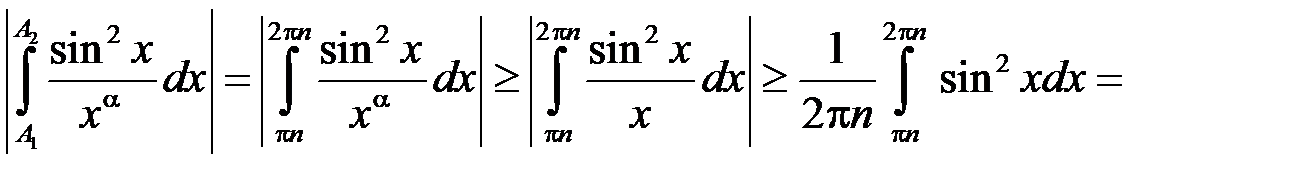
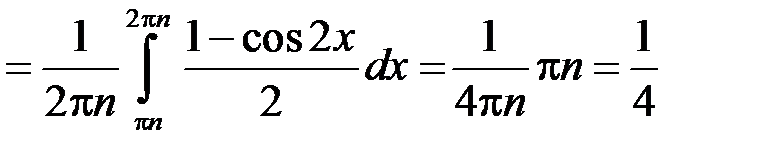 .
.
Таким чином можемо взяти 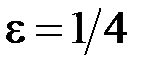 , і на підставі теореми 4 інтеграл розбіжний.
, і на підставі теореми 4 інтеграл розбіжний.
2. Дослідити на абсолютну та умовну збіжність інтеграл
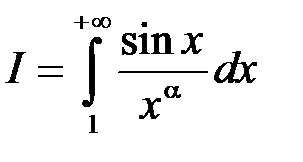 .
.
1) Нехай 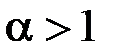 . Тоді
. Тоді 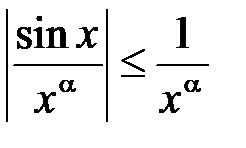 , і, оскільки інтеграл
, і, оскільки інтеграл 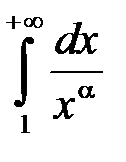 збіжний, то
збіжний, то
за теоремою 2 збіжним є інтеграл 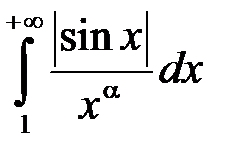 , отже інтеграл
, отже інтеграл 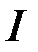 збіжний абсолютно.
збіжний абсолютно.
2) Нехай 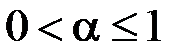 . Інтегруючи за частинами, отримаємо:
. Інтегруючи за частинами, отримаємо:
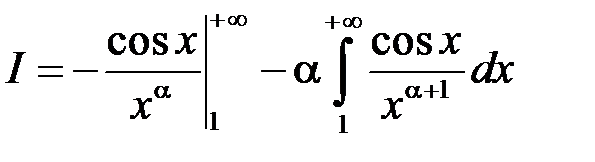 .
.
Оскільки 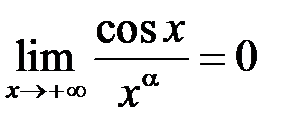 , а інтеграл
, а інтеграл 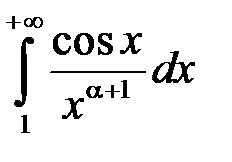 збіжний абсолютно, то
збіжний абсолютно, то 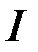 є збіжним.
є збіжним.
Розглянемо інтеграл 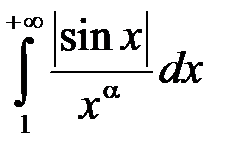 при
при 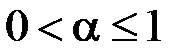 . Маємо:
. Маємо: 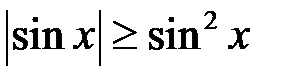 , а інтеграл
, а інтеграл 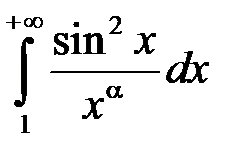 при
при 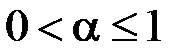 , як встановлено у попередньому прикладі, розбігається, отже розбігається й інтеграл
, як встановлено у попередньому прикладі, розбігається, отже розбігається й інтеграл 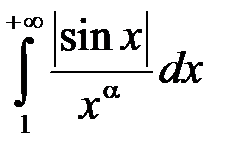 , а це означає, що інтеграл
, а це означає, що інтеграл 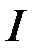 при
при 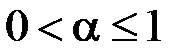 збігається умовно.
збігається умовно.
3) Нехай 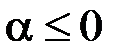 . Доведемо на підставі критерію Коші, що інтеграл
. Доведемо на підставі критерію Коші, що інтеграл 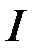
розбігається. Задамо 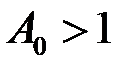 і оберемо
і оберемо 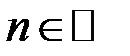 так, щоб
так, щоб 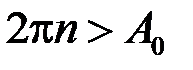 . Покладемо:
. Покладемо: 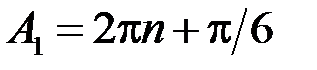 ,
, 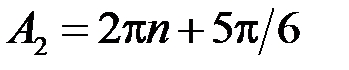 . Для
. Для 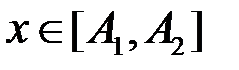 виконано
виконано 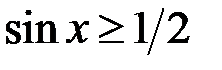 , і, крім того, при
, і, крім того, при 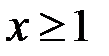 і
і 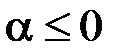 :
: 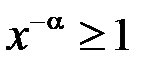 . Отже маємо:
. Отже маємо:
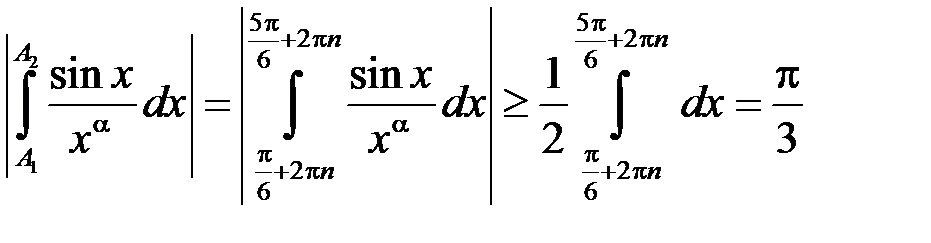 .
.
Таким чином, обираючи в критерії Коші 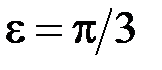 , отримуємо на його підставі, що інтеграл
, отримуємо на його підставі, що інтеграл 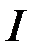 розбігається.
розбігається.
Отже інтеграл 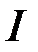 збігається абсолютно при
збігається абсолютно при 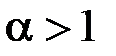 , збігається умовно при
, збігається умовно при 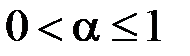 і розбігається при
і розбігається при 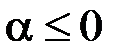 .
.


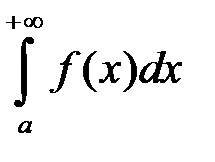 (11.1) необхідно і достатньо, щоб для будь якого
(11.1) необхідно і достатньо, щоб для будь якого 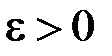 існувало таке число
існувало таке число 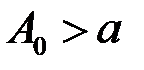 , щоб при
, щоб при 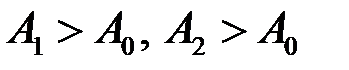 виконувалося нерівність:
виконувалося нерівність: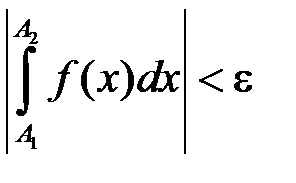 . (11.2)
. (11.2)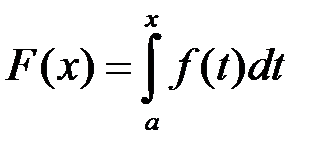 , умову теореми можна переписати так:
, умову теореми можна переписати так: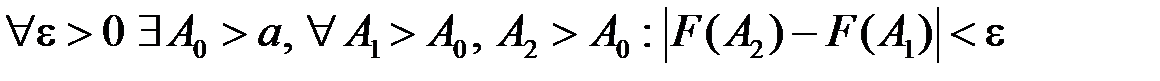 .
.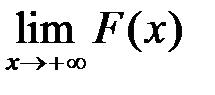 , тобто інтеграл (11.1) збігається тоді і тільки тоді, коли виконано нерівність (11.2).
, тобто інтеграл (11.1) збігається тоді і тільки тоді, коли виконано нерівність (11.2).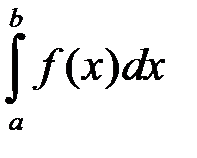 , (11.3)
, (11.3)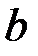 – особлива точка, необхідно і достатньо, щоб для будь якого
– особлива точка, необхідно і достатньо, щоб для будь якого 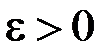 існувало
існувало 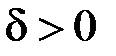 , що з нерівностей
, що з нерівностей 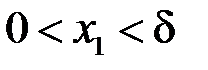 ,
, 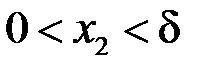 випливала нерівність
випливала нерівність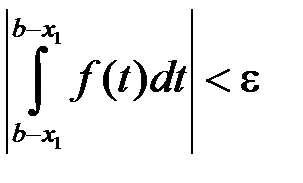 .
.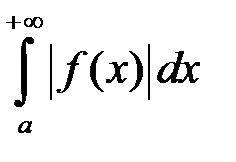 , то збігається інтег-
, то збігається інтег-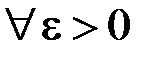
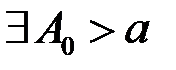 , що
, що 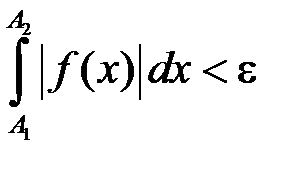 , якщо тільки
, якщо тільки 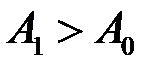 ,
, 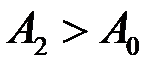 . Але
. Але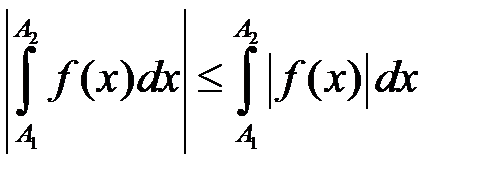 ,
,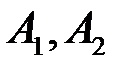 :
: 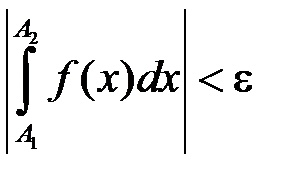 , звідки внаслідок теореми 4 випливає збіжність інтеграла (11.1).
, звідки внаслідок теореми 4 випливає збіжність інтеграла (11.1).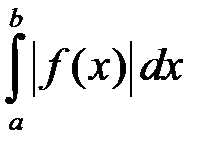 , де точка
, де точка 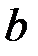 особлива, то збігається інтеграл (11.3).
особлива, то збігається інтеграл (11.3). 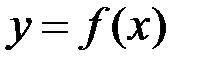 називається абсолютно збіжним, якщо збіжний інтеграл від функції
називається абсолютно збіжним, якщо збіжний інтеграл від функції 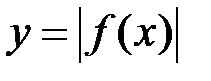 .
.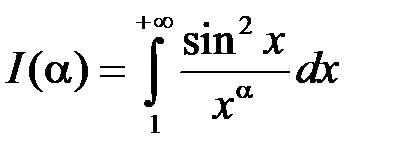 . (11.4)
. (11.4)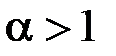 ; тоді
; тоді 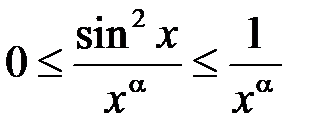 , і оскільки інтеграл
, і оскільки інтеграл 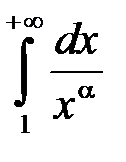 збігаєть-
збігаєть-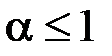 . Покажемо, що інтеграл (11.4) розбігається. Для цього
. Покажемо, що інтеграл (11.4) розбігається. Для цього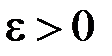 таке, що
таке, що 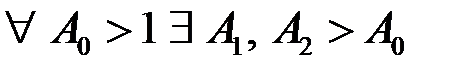 такі, що
такі, що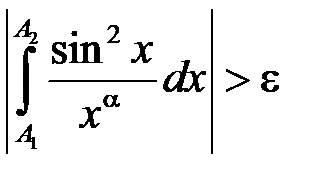 .
.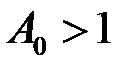 . Покладемо
. Покладемо 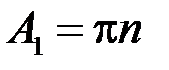 ,
, 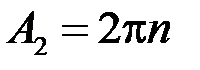 , де натуральне
, де натуральне 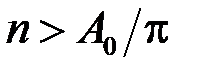 . Тоді, оскільки при
. Тоді, оскільки при 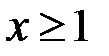 ,
, 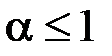 :
: 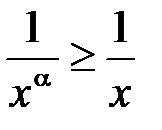 , то
, то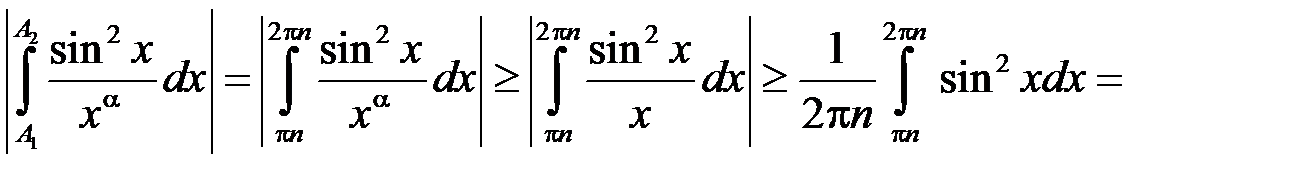
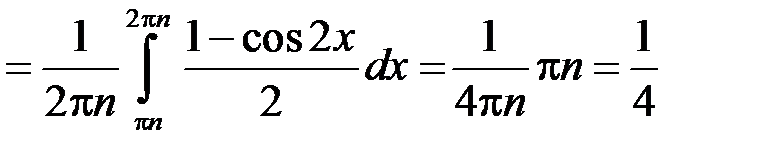 .
.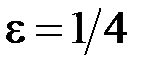 , і на підставі теореми 4 інтеграл розбіжний.
, і на підставі теореми 4 інтеграл розбіжний.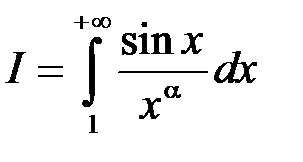 .
.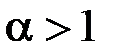 . Тоді
. Тоді 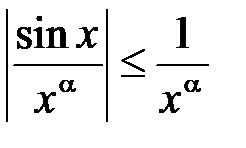 , і, оскільки інтеграл
, і, оскільки інтеграл 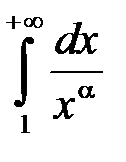 збіжний, то
збіжний, то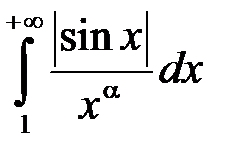 , отже інтеграл
, отже інтеграл 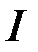 збіжний абсолютно.
збіжний абсолютно.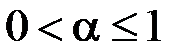 . Інтегруючи за частинами, отримаємо:
. Інтегруючи за частинами, отримаємо: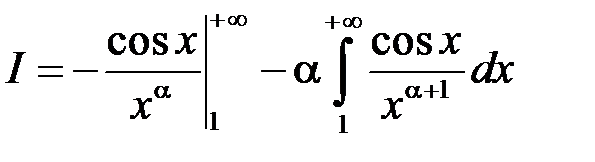 .
.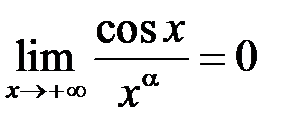 , а інтеграл
, а інтеграл 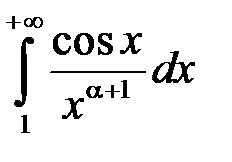 збіжний абсолютно, то
збіжний абсолютно, то 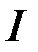 є збіжним.
є збіжним.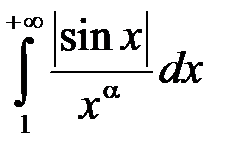 при
при 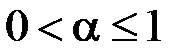 . Маємо:
. Маємо: 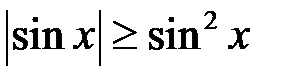 , а інтеграл
, а інтеграл 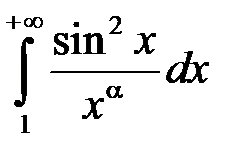 при
при 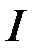 при
при 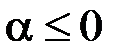 . Доведемо на підставі критерію Коші, що інтеграл
. Доведемо на підставі критерію Коші, що інтеграл 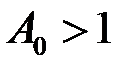 і оберемо
і оберемо 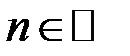 так, щоб
так, щоб 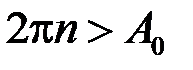 . Покладемо:
. Покладемо: 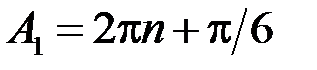 ,
, 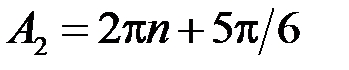 . Для
. Для 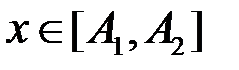 виконано
виконано 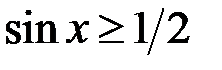 , і, крім того, при
, і, крім того, при 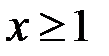 і
і 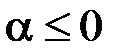 :
: 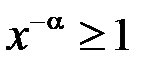 . Отже маємо:
. Отже маємо: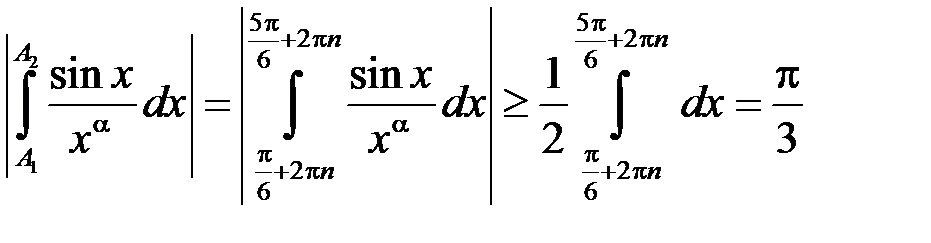 .
.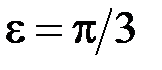 , отримуємо на його підставі, що інтеграл
, отримуємо на його підставі, що інтеграл 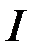 розбігається.
розбігається.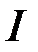 збігається абсолютно при
збігається абсолютно при 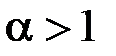 , збігається умовно при
, збігається умовно при 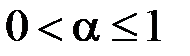 і розбігається при
і розбігається при