У багатьох випадках встановлювати збіжність інтеграла шляхом його безпосереднього обчислення досить складна задач. Тому якщо треба встановити тільки сам факт збіжності чи розбіжності, користуються деякими достатніми умовами збіжності.
Теорема 1. Нехай 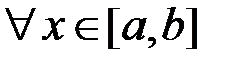 функція
функція 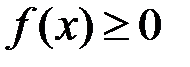 . Тоді для збіжності невласного інтеграла I роду
. Тоді для збіжності невласного інтеграла I роду 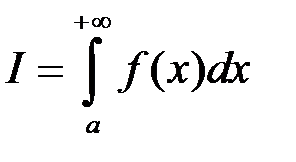 необхідно і достатньо, щоб функція
необхідно і достатньо, щоб функція 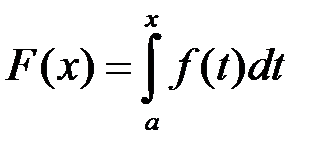 була обмежена зверху, тобто
була обмежена зверху, тобто 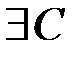 ,
, 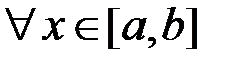 :
: 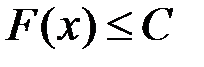 .
.
Доведення. Достатність. Нехай 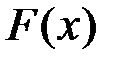 обмежена зверху. Оскільки
обмежена зверху. Оскільки 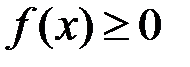 , то
, то 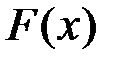 є неспадною, тобто монотонною. На підставі теореми про границю монотонної та обмеженої функції, існує
є неспадною, тобто монотонною. На підставі теореми про границю монотонної та обмеженої функції, існує 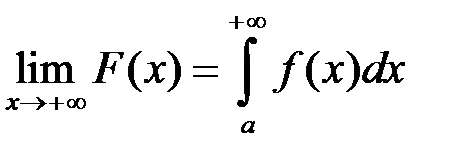 , тобто інтеграл
, тобто інтеграл 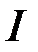 збіжний.
збіжний.
Необхідність. Нехай інтеграл 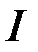 збіжний, тобто існує
збіжний, тобто існує 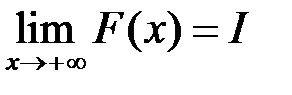 . Тоді на підставі тієї ж теореми про існування границі монотонної та обмеженої функції маємо:
. Тоді на підставі тієї ж теореми про існування границі монотонної та обмеженої функції маємо: 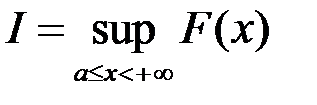 , і тоді
, і тоді  :
: 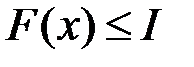 , тобто функція
, тобто функція 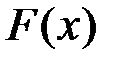 обмежена зверху.
обмежена зверху.
Теорема 2.Якщо на проміжку 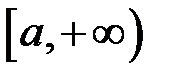 функції
функції 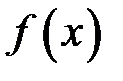 та
та 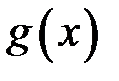 неперервні, та
неперервні, та 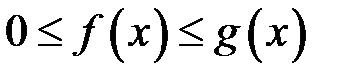 , то зі збіжності інтеграла
, то зі збіжності інтеграла
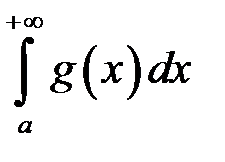 (10.1) випливає збіжність інтеграла
(10.1) випливає збіжність інтеграла
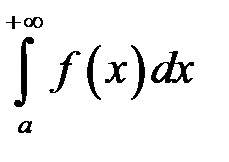 , (10.2) а з розбіжності інтеграла (10.2) випливає розбіжність інтеграла (10.1).
, (10.2) а з розбіжності інтеграла (10.2) випливає розбіжність інтеграла (10.1).
Доведення. I. Оскільки функції 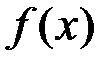 та
та 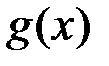 неперервні на
неперервні на 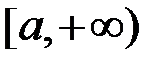 , вони інтегровні на будь якому проміжку
, вони інтегровні на будь якому проміжку 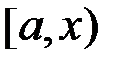 , де
, де 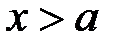 . Оскільки
. Оскільки 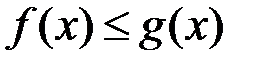 , то на підставі властивості 9 інтеграла маємо, що
, то на підставі властивості 9 інтеграла маємо, що 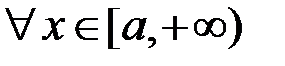 :
:
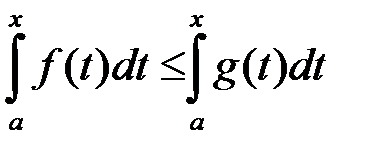 .
.
Оскільки інтеграл (10.1) збігається, то за теоремою 1 функція 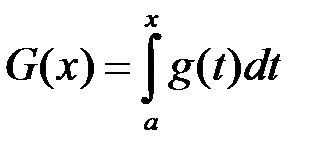 обмежена зверху, а тоді обмежена зверху й функція
обмежена зверху, а тоді обмежена зверху й функція 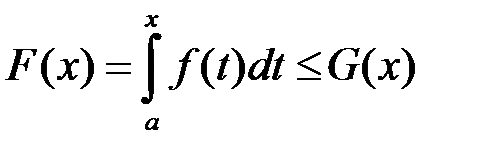 . Тоді на підставі теореми 1 існує
. Тоді на підставі теореми 1 існує 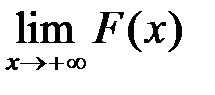 , тобто інтеграл (10.2) збіжний.
, тобто інтеграл (10.2) збіжний.
II. Якщо інтеграл (10.2) розбіжний, то розбіжним буде і інтеграл (10.1), оскільки в протилежному випадку на підставі I інтеграл був би збіжним.
Теорема 3.Якщо 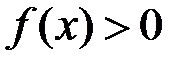 ,
, 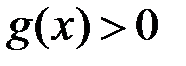
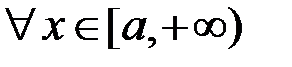 , та існує границя
, та існує границя
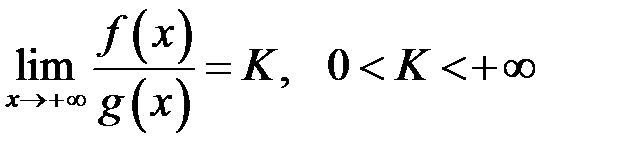 , то інтеграли (10.1), (10.2) водночас обидва збігаються, або водночас розбігаються.
, то інтеграли (10.1), (10.2) водночас обидва збігаються, або водночас розбігаються.
Доведення.Нехай збігається інтеграл (10.1). З умови теореми маємо:
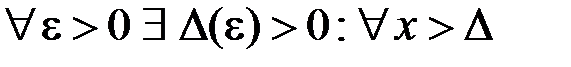 виконано
виконано 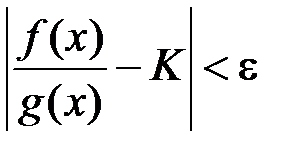 . Або, що те ж саме:
. Або, що те ж саме: 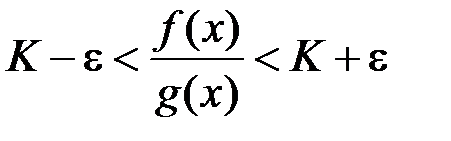 , звідки маємо
, звідки маємо 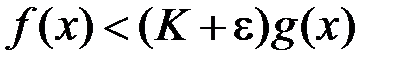 , якщо тільки
, якщо тільки 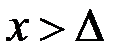 .
.
Оскільки
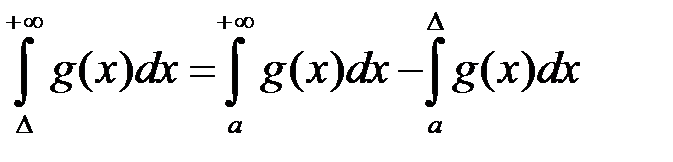 , то інтеграл
, то інтеграл 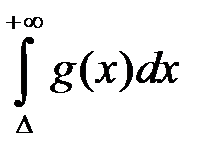 збіжний. Отже збіжний і інтеграл
збіжний. Отже збіжний і інтеграл 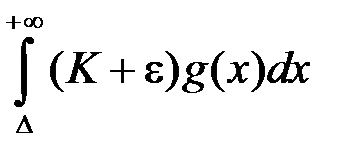 . Тоді за теоремою 2 є збіжним інтеграл
. Тоді за теоремою 2 є збіжним інтеграл 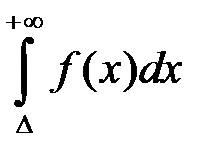 , а оскільки
, а оскільки
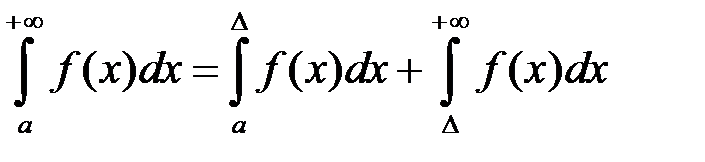 , то інтеграл (10.2) збіжний.
, то інтеграл (10.2) збіжний.
Переписавши умову теореми у вигляді:
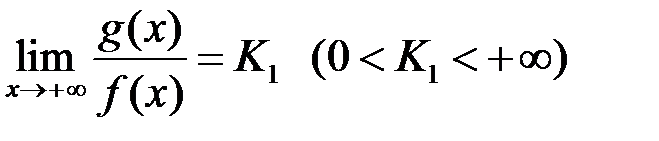 , де
, де 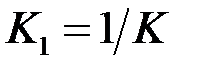 , отримаємо, що із збіжності інтеграла (10.2) випливає збіжність інтеграла (10.1). Таким чином інтеграли (10.1) та (10.2) збігаються та розбігаються водночас, а отже вони водночас і розбігаються.
, отримаємо, що із збіжності інтеграла (10.2) випливає збіжність інтеграла (10.1). Таким чином інтеграли (10.1) та (10.2) збігаються та розбігаються водночас, а отже вони водночас і розбігаються.
Теореми, аналогічні теоремам 1 – 3, мають місце і для невласних інтегралів II роду.
Приклади.
1. Дослідити на збіжність інтеграл
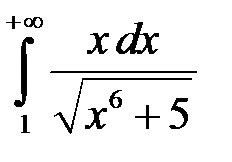 .
.
Маємо:
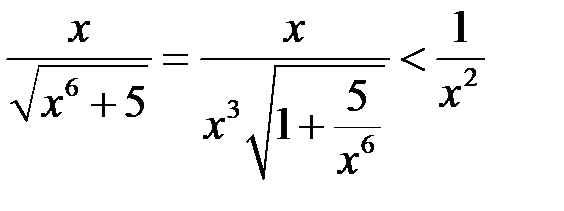 , а оскільки інтеграл
, а оскільки інтеграл
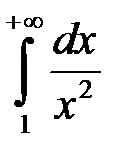 збігається (це інтеграл
збігається (це інтеграл 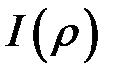 для
для  ), то згідно з теоремою 1 збігається і наш інтеграл.
), то згідно з теоремою 1 збігається і наш інтеграл.
2. Встановимо збіжність дуже важливого інтеграла Пуассона*:
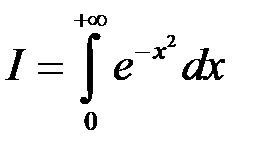 .
.
Зауважимо, що 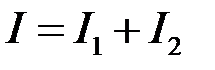 , де
, де
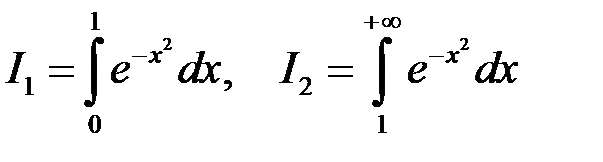 .
.
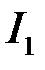 – це інтеграл від обмеженої функції на скінченному проміжку, і оскільки функція
– це інтеграл від обмеженої функції на скінченному проміжку, і оскільки функція 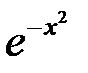 неперервна, інтеграл існує у власному розумінні. Стосовно другого інтеграла маємо:
неперервна, інтеграл існує у власному розумінні. Стосовно другого інтеграла маємо: 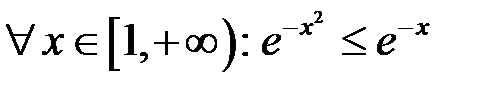 , а оскільки
, а оскільки
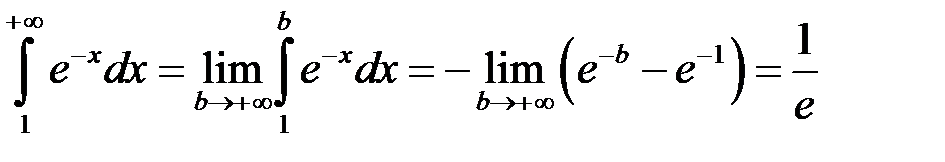 , тому цей інтеграл збіжний, отже збіжний за теоремою 1 інтеграл
, тому цей інтеграл збіжний, отже збіжний за теоремою 1 інтеграл  , а звідси випливає збіжність інтеграла
, а звідси випливає збіжність інтеграла 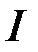 .
.
3. Дослідити на збіжність інтеграл
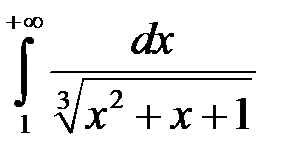 .
.
Маємо:
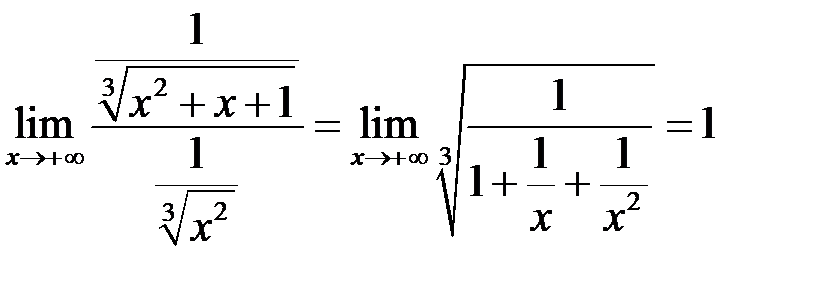 , і оскільки інтеграл
, і оскільки інтеграл
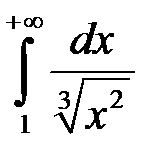 розбіжний (це інтеграл
розбіжний (це інтеграл 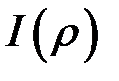 при
при 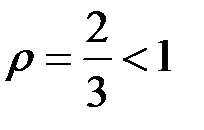 ), то внаслідок теореми 2 розбіжний і наш інтеграл.
), то внаслідок теореми 2 розбіжний і наш інтеграл.
4. Дослідити на збіжність інтеграл
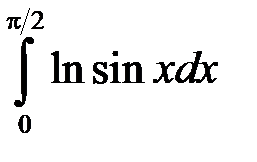 .
.
Особливою точкою є точка 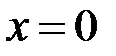 . Оскільки
. Оскільки
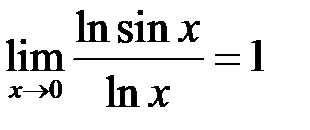 , то збіжність даного інтегралу рівносильна збіжності інтегралу
, то збіжність даного інтегралу рівносильна збіжності інтегралу 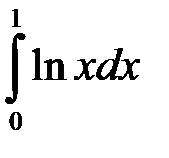 . Тому розглянемо:
. Тому розглянемо:
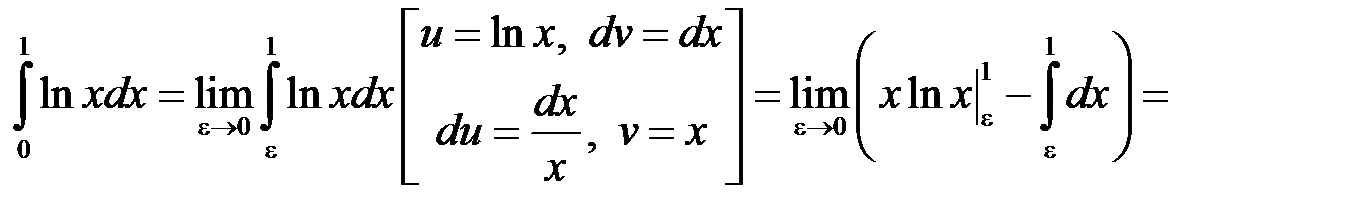
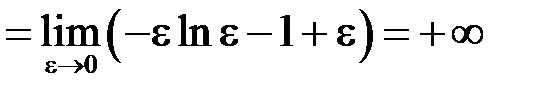 , тобто інтеграл розбіжний. А отже розбіжний і початковий інтеграл.
, тобто інтеграл розбіжний. А отже розбіжний і початковий інтеграл.
5. З’ясувати, при яких значеннях параметрів 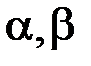 збігається, а при яких
збігається, а при яких
розбігається інтеграл:
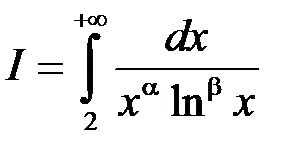 .
.
Розглянемо три можливі випадки: 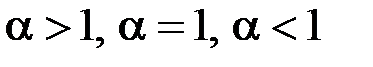 .
.
1) 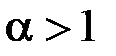 . Тоді
. Тоді 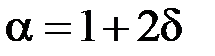 , де
, де 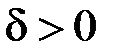 . Запишемо підінтегральну функцію у ви-
. Запишемо підінтегральну функцію у ви-
гляді:
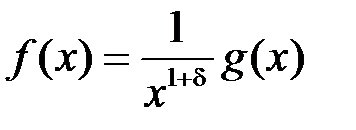 , де
, де 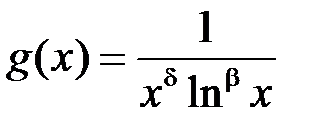 .
.
Оскільки 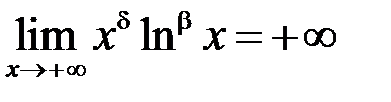 при
при 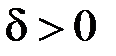 та
та 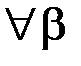 , то існує число
, то існує число 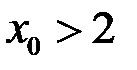 таке, що
таке, що 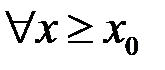 виконано:
виконано: 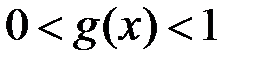 . Тому при
. Тому при 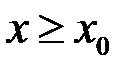 :
: 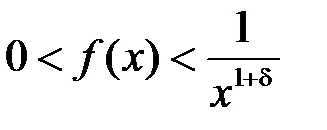 .
.
Інтеграл 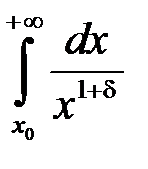 при
при 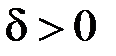 збіжний, отже за теоремою 2 збіжний й інтеграл
збіжний, отже за теоремою 2 збіжний й інтеграл 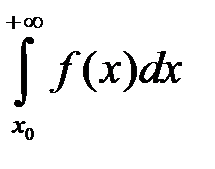 , а тоді збіжний й інтеграл
, а тоді збіжний й інтеграл 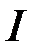 .
.
Таким чином, якщо 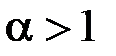 , то інтеграл
, то інтеграл 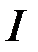 збіжний
збіжний 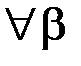 .
.
2) 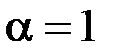 . Тоді
. Тоді
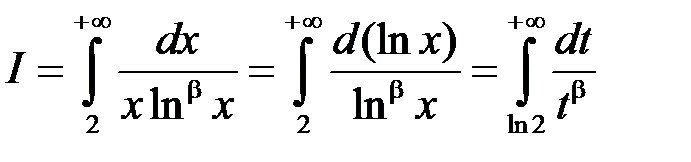 .
.
Цей інтеграл збіжний при 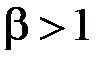 і розбіжний при
і розбіжний при 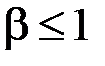 (приклад 5, п. 8).
(приклад 5, п. 8).
3) 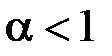 . Тоді
. Тоді 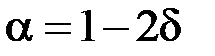 ,
, 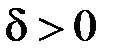 . Подамо підінтегральну функцію у вигляді:
. Подамо підінтегральну функцію у вигляді:
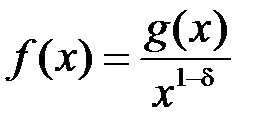 , де
, де 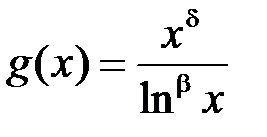 .
.
Маємо:
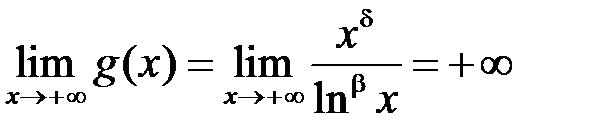 , отже існує число
, отже існує число 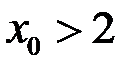 таке, що при
таке, що при 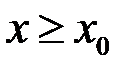 :
: 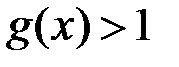 . Тому при
. Тому при 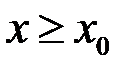 :
: 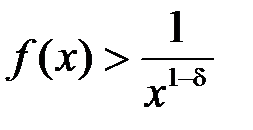 .
.
Інтеграл 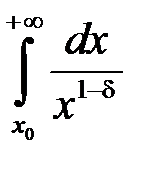 при
при 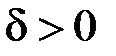 розбіжний, отже за теоремою 2 розбіжним буде й інтеграл
розбіжний, отже за теоремою 2 розбіжним буде й інтеграл 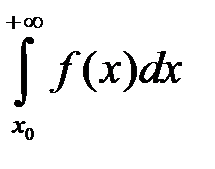 , а тоді розбіжним буде й інтеграл
, а тоді розбіжним буде й інтеграл 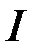 .
.
Таким чином інтеграл 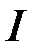 збігається при
збігається при 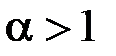 (
( 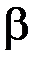 будь яке), при
будь яке), при 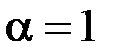 ,
, 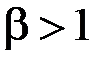 , і розбігається при всіх інших
, і розбігається при всіх інших 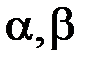 .
.
6. Дослідити на збіжність інтеграл:
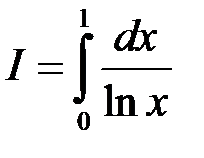 .
.
Цей невласний інтеграл II роду має дві особливі точки 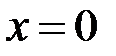 та
та 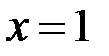 .
.
Подамо інтеграл у вигляді 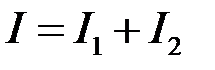 , де
, де
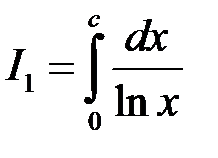 ,
, 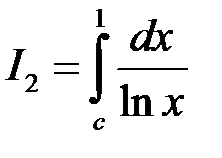 ,
,
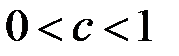 , і дослідимо окремо збіжність кожного з цих інтегралів.
, і дослідимо окремо збіжність кожного з цих інтегралів.
а) 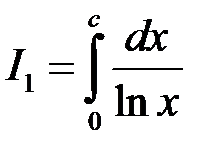 .
.
Зробимо заміну змінної 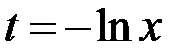 . Тоді, якщо
. Тоді, якщо 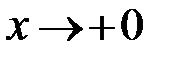 , то
, то 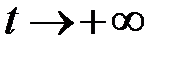 , і при
, і при 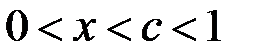 :
: 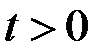 ;
; 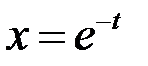 ,
, 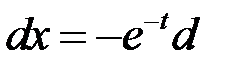 , і інтеграл II роду перетворюється на інтеграл I роду:
, і інтеграл II роду перетворюється на інтеграл I роду:
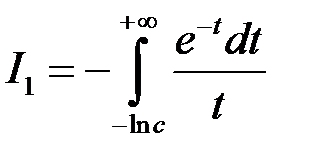 .
.
Розглянемо інтеграл
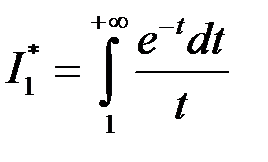 .
.
При 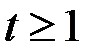 :
: 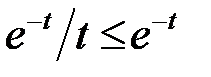 . Інтеграл
. Інтеграл 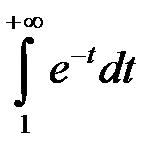 збіжний, він дорівнює
збіжний, він дорівнює 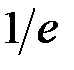 . Тоді за теоремою 2 збіжний й інтеграл
. Тоді за теоремою 2 збіжний й інтеграл 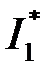 , отже збіжний й інтеграл
, отже збіжний й інтеграл 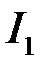 .
.
б) 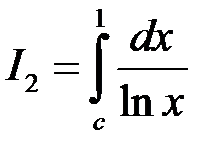 .
.
При 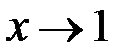 :
: 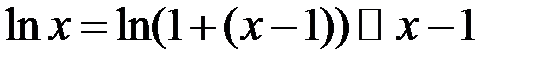 , тобто
, тобто 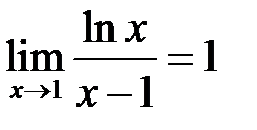 . Розглянемо
. Розглянемо
інтеграл
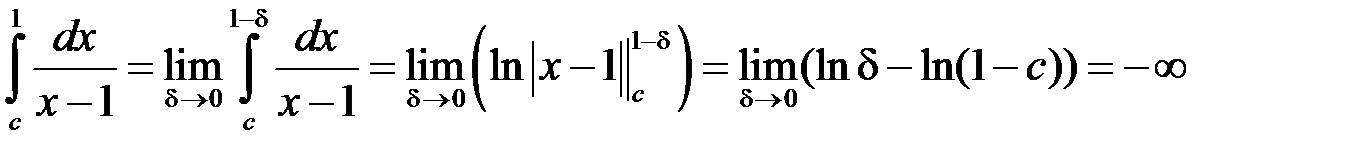 ,
,
отже за теоремою 3 є розбіжним інтеграл 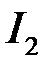 . А тоді інтеграл
. А тоді інтеграл 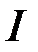 також розбіжний.
також розбіжний.


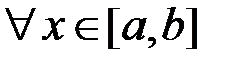 функція
функція 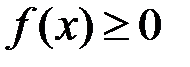 . Тоді для збіжності невласного інтеграла I роду
. Тоді для збіжності невласного інтеграла I роду 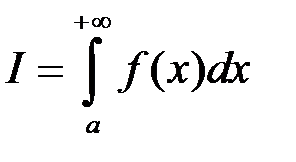 необхідно і достатньо, щоб функція
необхідно і достатньо, щоб функція 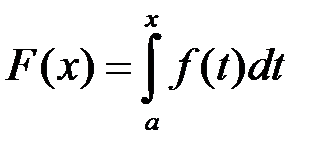 була обмежена зверху, тобто
була обмежена зверху, тобто 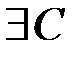 ,
, 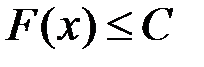 .
.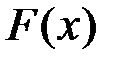 обмежена зверху. Оскільки
обмежена зверху. Оскільки 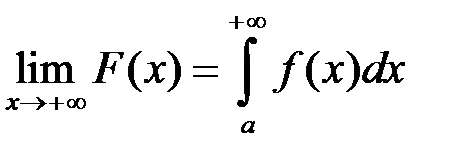 , тобто інтеграл
, тобто інтеграл 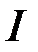 збіжний.
збіжний.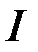 збіжний, тобто існує
збіжний, тобто існує 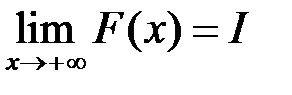 . Тоді на підставі тієї ж теореми про існування границі монотонної та обмеженої функції маємо:
. Тоді на підставі тієї ж теореми про існування границі монотонної та обмеженої функції маємо: 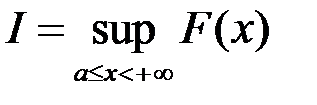 , і тоді
, і тоді 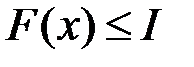 , тобто функція
, тобто функція 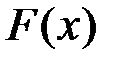 обмежена зверху.
обмежена зверху.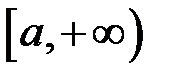 функції
функції 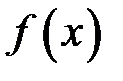 та
та 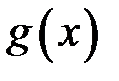 неперервні, та
неперервні, та 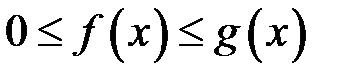 , то зі збіжності інтеграла
, то зі збіжності інтеграла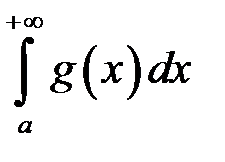 (10.1) випливає збіжність інтеграла
(10.1) випливає збіжність інтеграла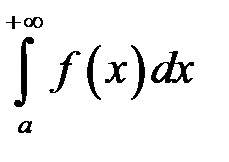 , (10.2) а з розбіжності інтеграла (10.2) випливає розбіжність інтеграла (10.1).
, (10.2) а з розбіжності інтеграла (10.2) випливає розбіжність інтеграла (10.1).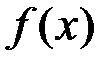 та
та 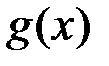 неперервні на
неперервні на 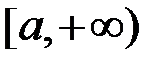 , вони інтегровні на будь якому проміжку
, вони інтегровні на будь якому проміжку 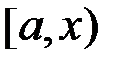 , де
, де 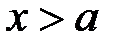 . Оскільки
. Оскільки 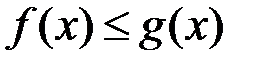 , то на підставі властивості 9 інтеграла маємо, що
, то на підставі властивості 9 інтеграла маємо, що 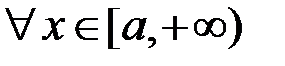 :
: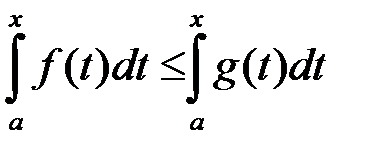 .
.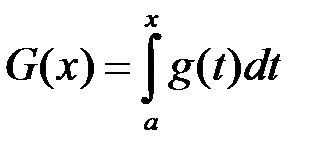 обмежена зверху, а тоді обмежена зверху й функція
обмежена зверху, а тоді обмежена зверху й функція 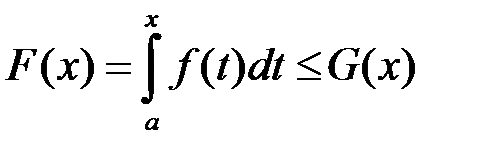 . Тоді на підставі теореми 1 існує
. Тоді на підставі теореми 1 існує 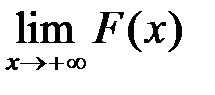 , тобто інтеграл (10.2) збіжний.
, тобто інтеграл (10.2) збіжний.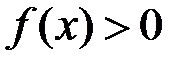 ,
, 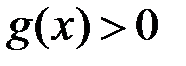
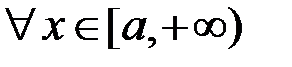 , та існує границя
, та існує границя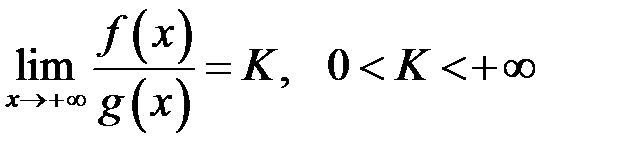 , то інтеграли (10.1), (10.2) водночас обидва збігаються, або водночас розбігаються.
, то інтеграли (10.1), (10.2) водночас обидва збігаються, або водночас розбігаються.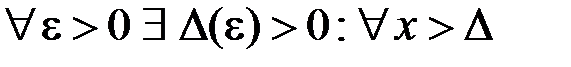 виконано
виконано 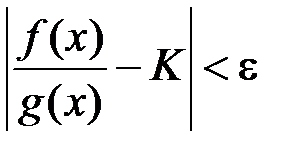 . Або, що те ж саме:
. Або, що те ж саме: 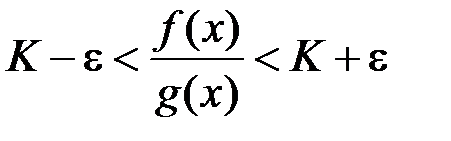 , звідки маємо
, звідки маємо 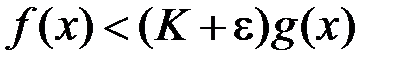 , якщо тільки
, якщо тільки 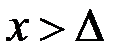 .
.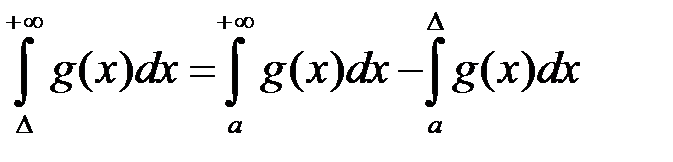 , то інтеграл
, то інтеграл 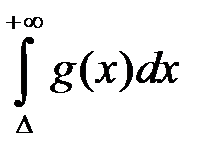 збіжний. Отже збіжний і інтеграл
збіжний. Отже збіжний і інтеграл 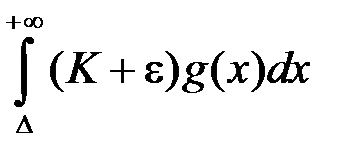 . Тоді за теоремою 2 є збіжним інтеграл
. Тоді за теоремою 2 є збіжним інтеграл 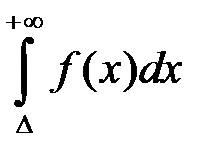 , а оскільки
, а оскільки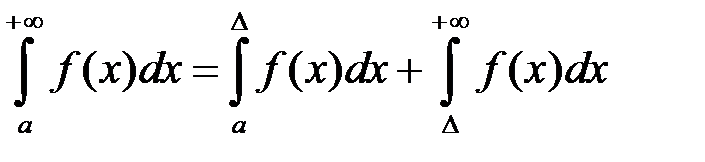 , то інтеграл (10.2) збіжний.
, то інтеграл (10.2) збіжний.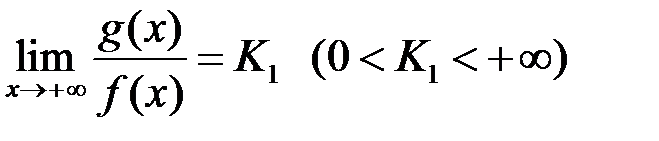 , де
, де 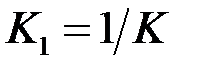 , отримаємо, що із збіжності інтеграла (10.2) випливає збіжність інтеграла (10.1). Таким чином інтеграли (10.1) та (10.2) збігаються та розбігаються водночас, а отже вони водночас і розбігаються.
, отримаємо, що із збіжності інтеграла (10.2) випливає збіжність інтеграла (10.1). Таким чином інтеграли (10.1) та (10.2) збігаються та розбігаються водночас, а отже вони водночас і розбігаються.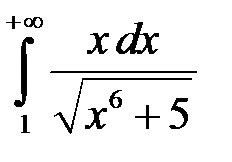 .
.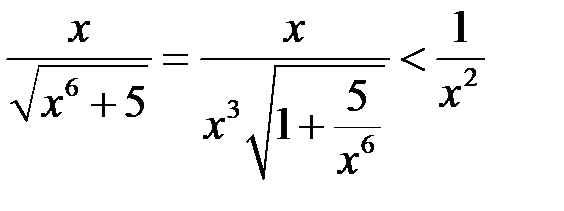 , а оскільки інтеграл
, а оскільки інтеграл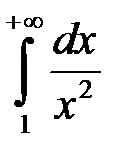 збігається (це інтеграл
збігається (це інтеграл  для
для 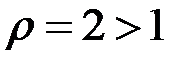 ), то згідно з теоремою 1 збігається і наш інтеграл.
), то згідно з теоремою 1 збігається і наш інтеграл.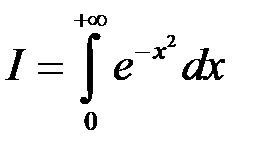 .
.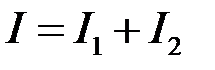 , де
, де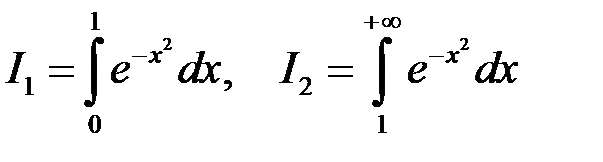 .
.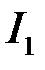 – це інтеграл від обмеженої функції на скінченному проміжку, і оскільки функція
– це інтеграл від обмеженої функції на скінченному проміжку, і оскільки функція 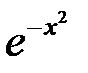 неперервна, інтеграл існує у власному розумінні. Стосовно другого інтеграла маємо:
неперервна, інтеграл існує у власному розумінні. Стосовно другого інтеграла маємо: 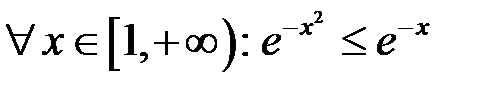 , а оскільки
, а оскільки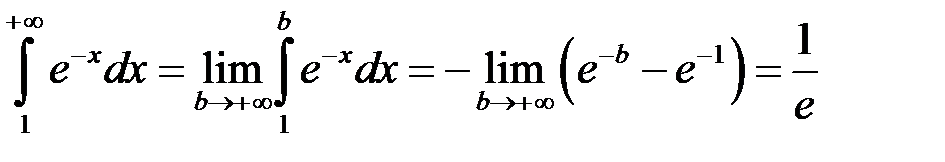 , тому цей інтеграл збіжний, отже збіжний за теоремою 1 інтеграл
, тому цей інтеграл збіжний, отже збіжний за теоремою 1 інтеграл  , а звідси випливає збіжність інтеграла
, а звідси випливає збіжність інтеграла 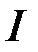 .
.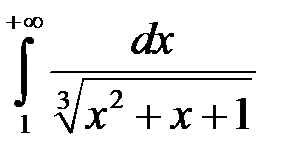 .
.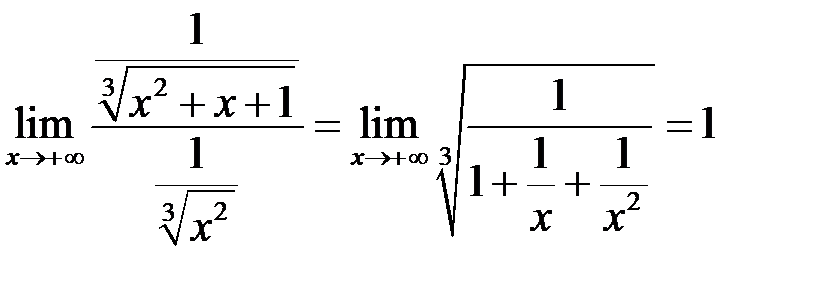 , і оскільки інтеграл
, і оскільки інтеграл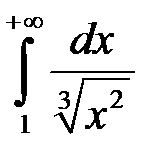 розбіжний (це інтеграл
розбіжний (це інтеграл 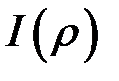 при
при 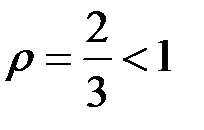 ), то внаслідок теореми 2 розбіжний і наш інтеграл.
), то внаслідок теореми 2 розбіжний і наш інтеграл.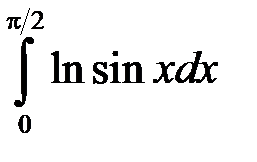 .
.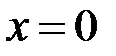 . Оскільки
. Оскільки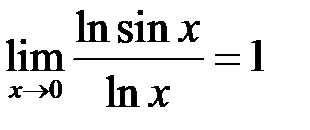 , то збіжність даного інтегралу рівносильна збіжності інтегралу
, то збіжність даного інтегралу рівносильна збіжності інтегралу 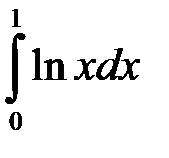 . Тому розглянемо:
. Тому розглянемо: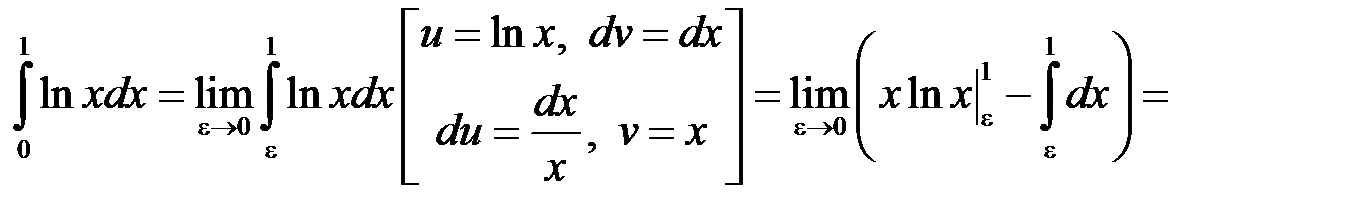
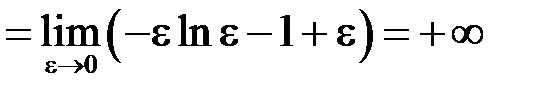 , тобто інтеграл розбіжний. А отже розбіжний і початковий інтеграл.
, тобто інтеграл розбіжний. А отже розбіжний і початковий інтеграл.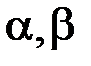 збігається, а при яких
збігається, а при яких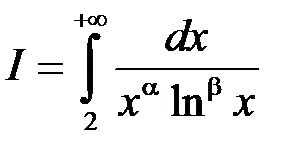 .
. .
. . Тоді
. Тоді 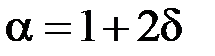 , де
, де 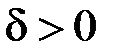 . Запишемо підінтегральну функцію у ви-
. Запишемо підінтегральну функцію у ви-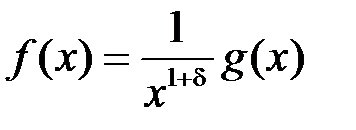 , де
, де 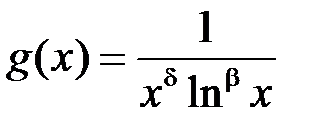 .
.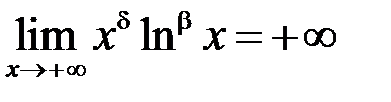 при
при 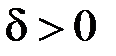 та
та 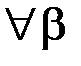 , то існує число
, то існує число 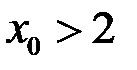 таке, що
таке, що 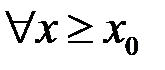 виконано:
виконано: 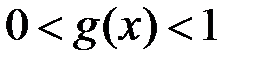 . Тому при
. Тому при 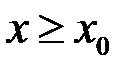 :
: 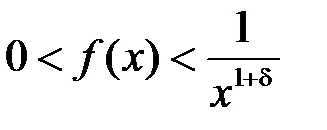 .
.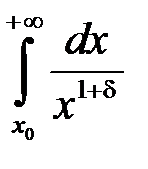 при
при 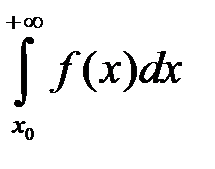 , а тоді збіжний й інтеграл
, а тоді збіжний й інтеграл  .
. , то інтеграл
, то інтеграл 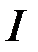 збіжний
збіжний 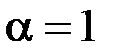 . Тоді
. Тоді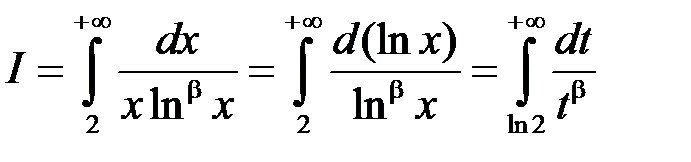 .
.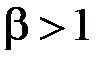 і розбіжний при
і розбіжний при 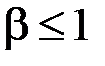 (приклад 5, п. 8).
(приклад 5, п. 8).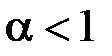 . Тоді
. Тоді 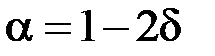 ,
, 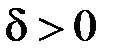 . Подамо підінтегральну функцію у вигляді:
. Подамо підінтегральну функцію у вигляді: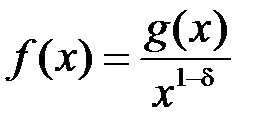 , де
, де 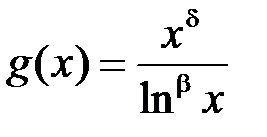 .
.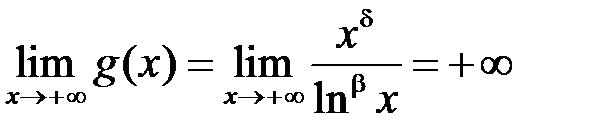 , отже існує число
, отже існує число 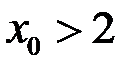 таке, що при
таке, що при 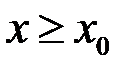 :
: 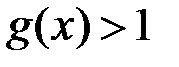 . Тому при
. Тому при 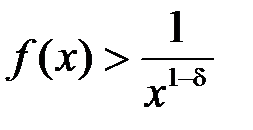 .
.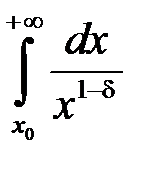 при
при 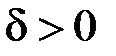 розбіжний, отже за теоремою 2 розбіжним буде й інтеграл
розбіжний, отже за теоремою 2 розбіжним буде й інтеграл 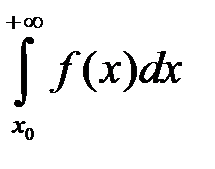 , а тоді розбіжним буде й інтеграл
, а тоді розбіжним буде й інтеграл 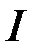 .
.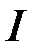 збігається при
збігається при 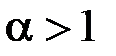 (
( 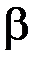 будь яке), при
будь яке), при 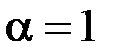 ,
, 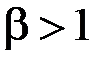 , і розбігається при всіх інших
, і розбігається при всіх інших 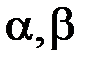 .
.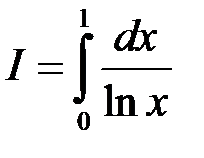 .
.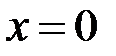 та
та 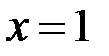 .
.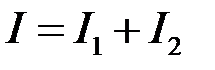 , де
, де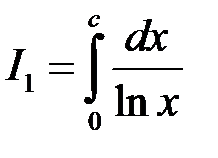 ,
, 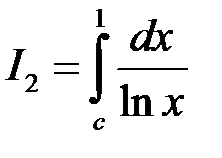 ,
,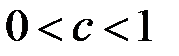 , і дослідимо окремо збіжність кожного з цих інтегралів.
, і дослідимо окремо збіжність кожного з цих інтегралів.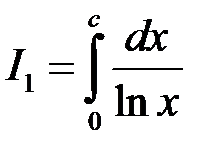 .
.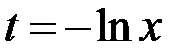 . Тоді, якщо
. Тоді, якщо 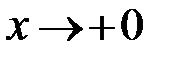 , то
, то 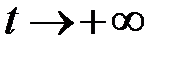 , і при
, і при 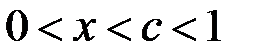 :
: 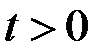 ;
; 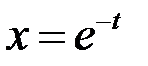 ,
, 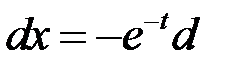 , і інтеграл II роду перетворюється на інтеграл I роду:
, і інтеграл II роду перетворюється на інтеграл I роду: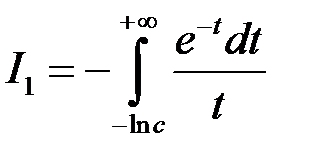 .
.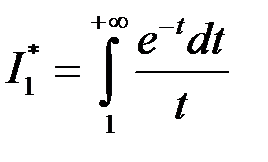 .
. :
: 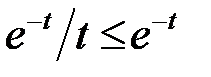 . Інтеграл
. Інтеграл 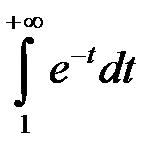 збіжний, він дорівнює
збіжний, він дорівнює 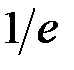 . Тоді за теоремою 2 збіжний й інтеграл
. Тоді за теоремою 2 збіжний й інтеграл 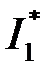 , отже збіжний й інтеграл
, отже збіжний й інтеграл 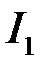 .
.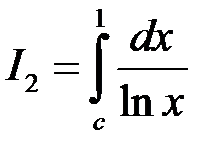 .
. :
: 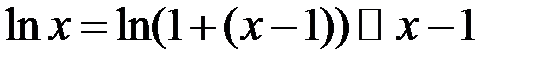 , тобто
, тобто 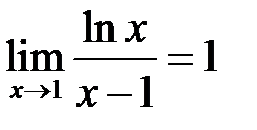 . Розглянемо
. Розглянемо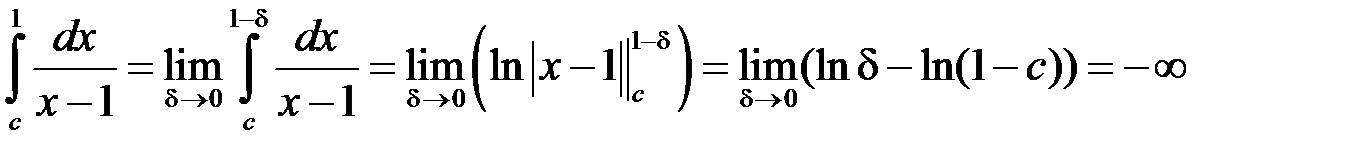 ,
, . А тоді інтеграл
. А тоді інтеграл  також розбіжний.
також розбіжний.