Розглянемо тепер функцію 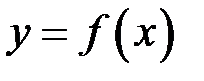 , яка визначена на півінтервалі
, яка визначена на півінтервалі 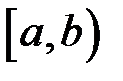 , і нехай виконана умова:
, і нехай виконана умова:
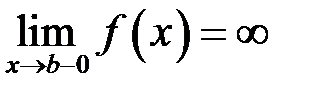 (9.1)
(9.1)
Точку 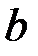 будемо називати особливою точкою функції
будемо називати особливою точкою функції 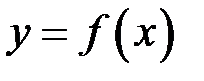 . У цій точці графік функції має вертикальну асимптоту (рис. 6).
. У цій точці графік функції має вертикальну асимптоту (рис. 6).
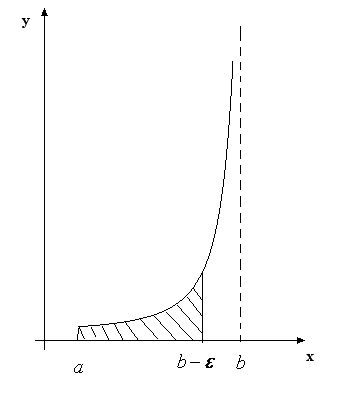
Рис. 6.
Нехай функція 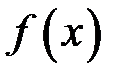 інтегровна на будь якому проміжку
інтегровна на будь якому проміжку 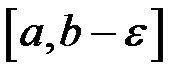 , де
, де 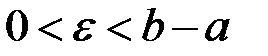 .
.
Означення.Невласним інтегралом II роду від функції 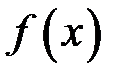 називається границя:
називається границя:
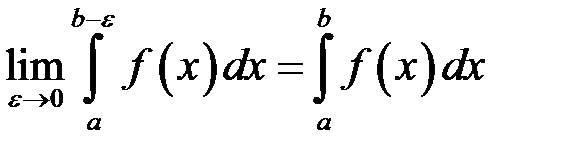 . (9.2)
. (9.2)
Якщо границя (9.2) існує і скінченна, то інтеграл називається збіжним, у протилежному випадку – розбіжним.
Якщо особливою точкою функції 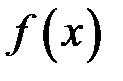 є точка
є точка 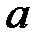 , то:
, то:
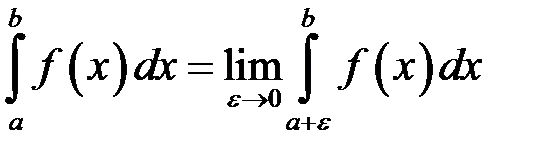 . при умові, що функція
. при умові, що функція 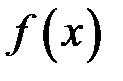 інтегровна на проміжку
інтегровна на проміжку 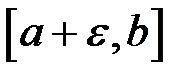 , де також
, де також 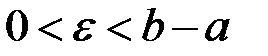 .
.
Нарешті, якщо особливою точкою є деяка точка 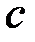 всередині проміжку
всередині проміжку 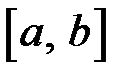 , то за означенням покладають:
, то за означенням покладають:
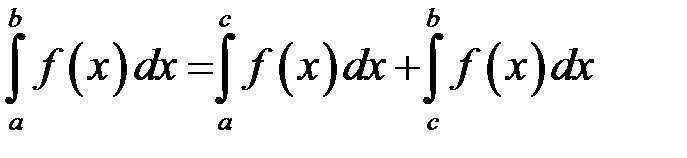 . (9.3)
. (9.3)
Якщо існують окремо скінченні границі
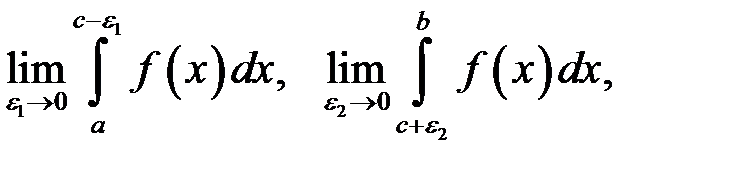 то інтеграл у лівій частині рівності (8.8.3) називається збіжним, а якщо хоч би одна з цих границь не існує, або нескінченна – розбіжним.
то інтеграл у лівій частині рівності (8.8.3) називається збіжним, а якщо хоч би одна з цих границь не існує, або нескінченна – розбіжним.
Якщо особливими являються точки 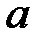 і
і 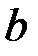 , то за означенням:
, то за означенням:
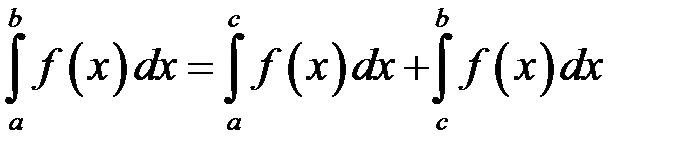 , де
, де 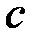 – довільна точка інтервалу
– довільна точка інтервалу 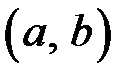 . Інтеграл у лівій частині рівності буде збіжним тоді і тільки тоді, коли збіжні обидва інтеграли у правій частині рівності.
. Інтеграл у лівій частині рівності буде збіжним тоді і тільки тоді, коли збіжні обидва інтеграли у правій частині рівності.
З геометричної точки зору інтеграл II роду (9.2) також, як і невласний інтеграл I роду, виражає площу нескінченної фігури (рис. 7).
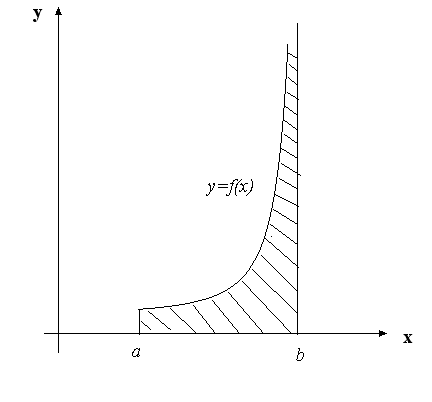
Рис. 7.
Але якщо у випадку інтеграла I роду нескінченність, так кажучи, відносно осі 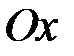 (рис. 5), то тут – відносно осі
(рис. 5), то тут – відносно осі 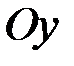 . Фактично це така ж сама нескінченна криволінійна трапеція, тільки повернута на кут 90 градусів. А це свідчить про те, що між невласними інтегралами I та II роду існує певний зв’язок. Дійсно, нехай, наприклад, особливою точкою функції
. Фактично це така ж сама нескінченна криволінійна трапеція, тільки повернута на кут 90 градусів. А це свідчить про те, що між невласними інтегралами I та II роду існує певний зв’язок. Дійсно, нехай, наприклад, особливою точкою функції 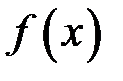 є точка
є точка 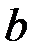 . Тоді
. Тоді
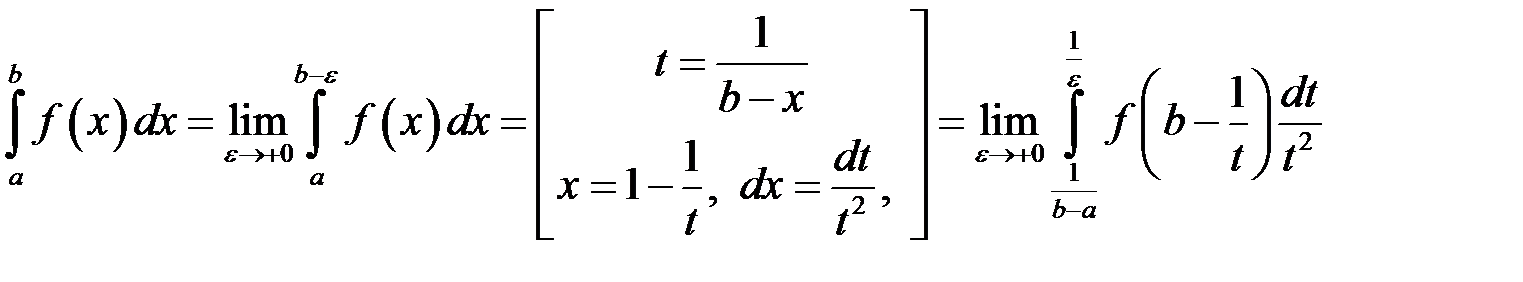 .
.
У останньому інтегралі позначимо:
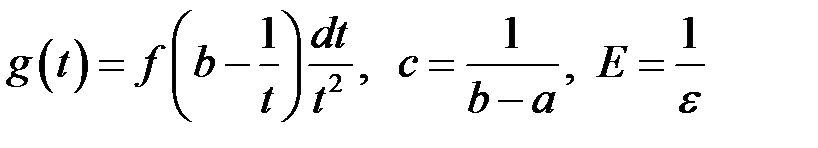 .
.
Якщо 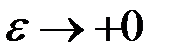 , то очевидно
, то очевидно 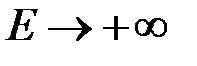 , і ми отримуємо:
, і ми отримуємо:
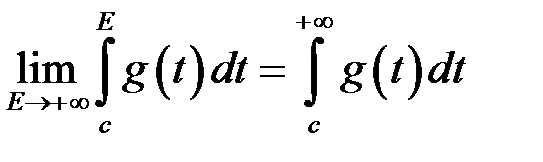 .
.
Таким чином звели невласний інтеграл II роду до невласного інтегралу I роду.
Приклади. Дослідити на збіжність і у випадку збіжності обчислити інтеграли.
1) 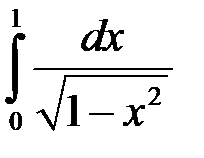 .
.
У даному прикладі особливою є точка 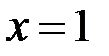 . Маємо:
. Маємо:
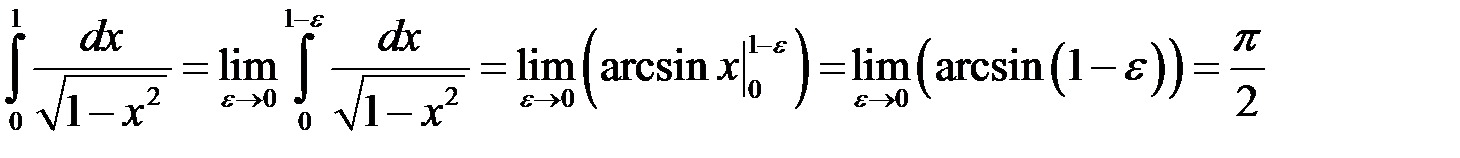 .
.
Отже інтеграл збіжний, і його значення дорівнює 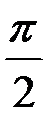 .
.
2) 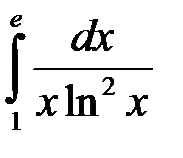 .
.
Особливою є точка 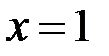 , оскільки
, оскільки 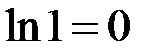 . Маємо:
. Маємо:
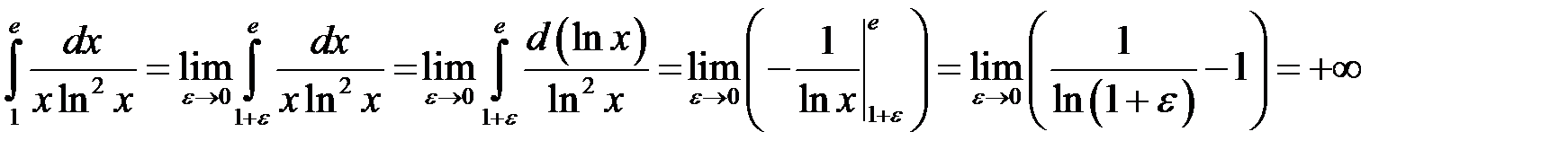
Отже інтеграл розбіжний.
3) Встановити, для яких значень параметра 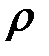 інтеграл збігається, а дл яких розбігається:
інтеграл збігається, а дл яких розбігається:
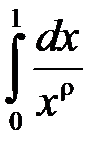 .
.
Якщо 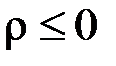 , то інтеграл не є невласним, оскільки підінтегральна функція
, то інтеграл не є невласним, оскільки підінтегральна функція 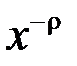 буде обмеженою на відрізку
буде обмеженою на відрізку 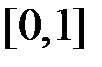 . Отже залишилось дослідити випадок
. Отже залишилось дослідити випадок 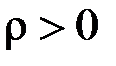 . Тоді особливою точкою буде точка
. Тоді особливою точкою буде точка 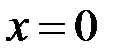 . Нехай спочатку
. Нехай спочатку 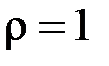 . Маємо:
. Маємо:
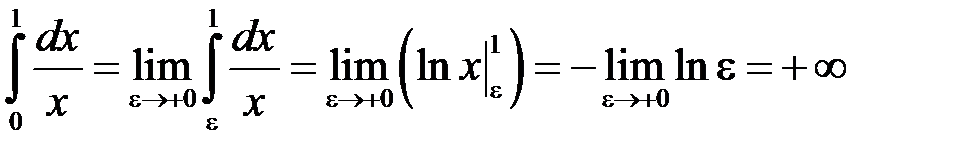 , отже інтеграл розбіжний. Нехай тепер
, отже інтеграл розбіжний. Нехай тепер 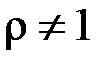 . Тоді:
. Тоді:
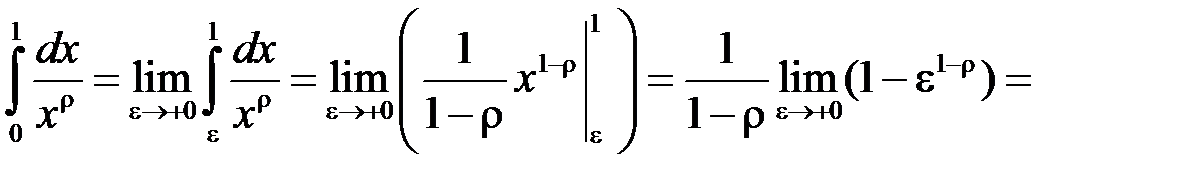
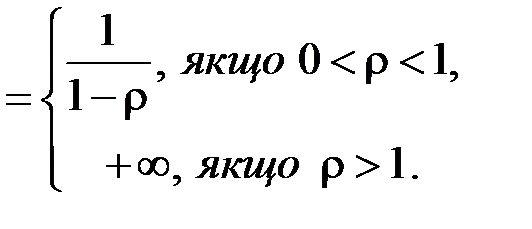
Отже інтеграл збігається, якщо 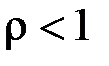 , і розбігається, якщо
, і розбігається, якщо 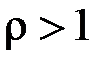 .
.
Повернемось до прикладу, який ми розглянули в п. 6, а саме до інтегралу
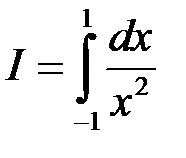 .
.
Ми встановили, що безпосереднє використання формули Ньютона – Лейбніца приводить до абсурдного результату – інтеграл дорівнює від’ємному числу, хоча зобов’язаний бути додатним. Тепер ми можемо сказати, що цей інтеграл невласний – особливою є точка 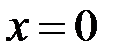 , яка належить інтервалу
, яка належить інтервалу 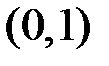 . Розіб’ємо цей інтеграл на два інтеграли
. Розіб’ємо цей інтеграл на два інтеграли
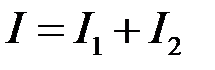 , де
, де
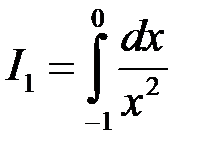 ,
, 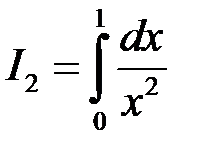 .
.
Оскільки, як було встановлено в прикладі 3), інтеграл  розбіжний, то розбіжним буде й інтеграл
розбіжний, то розбіжним буде й інтеграл 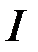 . Таким чином про його обчислення взагалі не може йти мова.
. Таким чином про його обчислення взагалі не може йти мова.


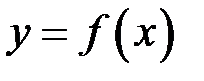 , яка визначена на півінтервалі
, яка визначена на півінтервалі 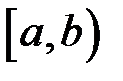 , і нехай виконана умова:
, і нехай виконана умова: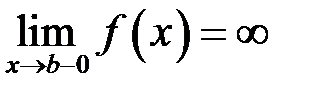 (9.1)
(9.1)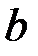 будемо називати особливою точкою функції
будемо називати особливою точкою функції 
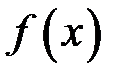 інтегровна на будь якому проміжку
інтегровна на будь якому проміжку 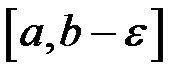 , де
, де 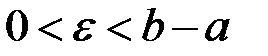 .
.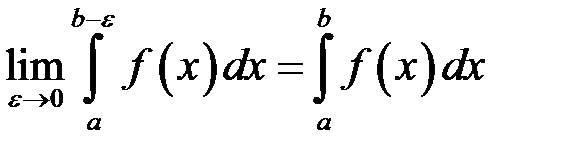 . (9.2)
. (9.2)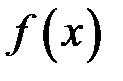 є точка
є точка 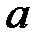 , то:
, то: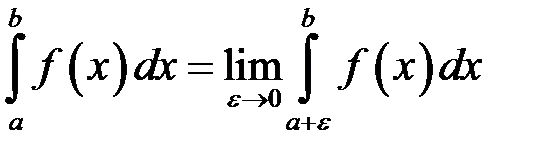 . при умові, що функція
. при умові, що функція 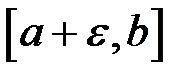 , де також
, де також 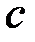 всередині проміжку
всередині проміжку 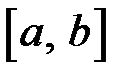 , то за означенням покладають:
, то за означенням покладають: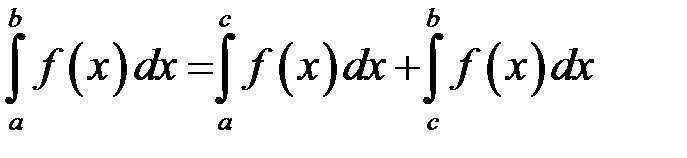 . (9.3)
. (9.3)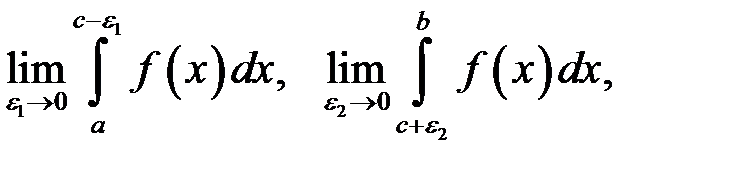 то інтеграл у лівій частині рівності (8.8.3) називається збіжним, а якщо хоч би одна з цих границь не існує, або нескінченна – розбіжним.
то інтеграл у лівій частині рівності (8.8.3) називається збіжним, а якщо хоч би одна з цих границь не існує, або нескінченна – розбіжним.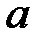 і
і 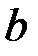 , то за означенням:
, то за означенням: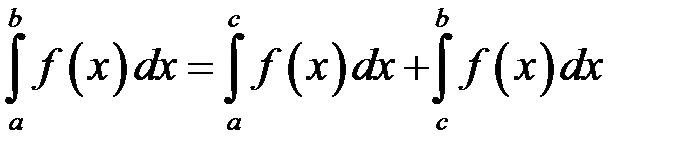 , де
, де 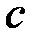 – довільна точка інтервалу
– довільна точка інтервалу 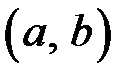 . Інтеграл у лівій частині рівності буде збіжним тоді і тільки тоді, коли збіжні обидва інтеграли у правій частині рівності.
. Інтеграл у лівій частині рівності буде збіжним тоді і тільки тоді, коли збіжні обидва інтеграли у правій частині рівності.
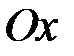 (рис. 5), то тут – відносно осі
(рис. 5), то тут – відносно осі 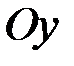 . Фактично це така ж сама нескінченна криволінійна трапеція, тільки повернута на кут 90 градусів. А це свідчить про те, що між невласними інтегралами I та II роду існує певний зв’язок. Дійсно, нехай, наприклад, особливою точкою функції
. Фактично це така ж сама нескінченна криволінійна трапеція, тільки повернута на кут 90 градусів. А це свідчить про те, що між невласними інтегралами I та II роду існує певний зв’язок. Дійсно, нехай, наприклад, особливою точкою функції 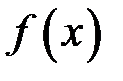 є точка
є точка 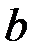 . Тоді
. Тоді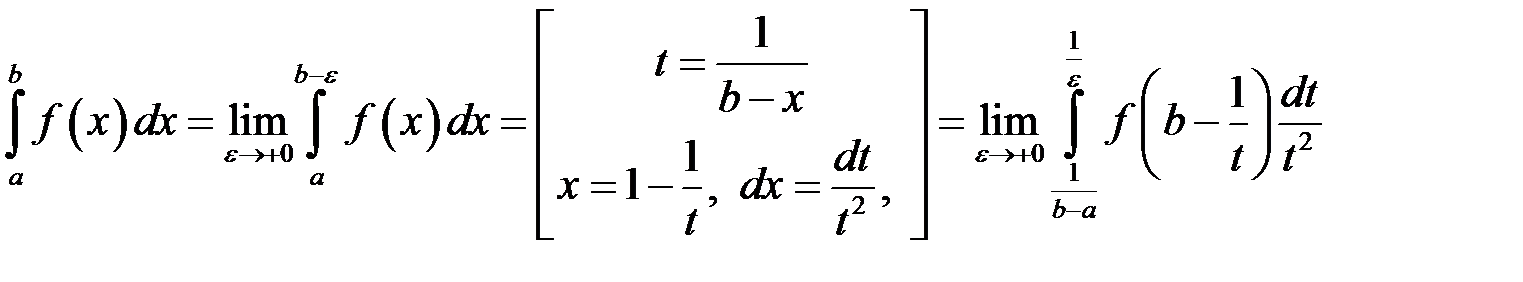 .
.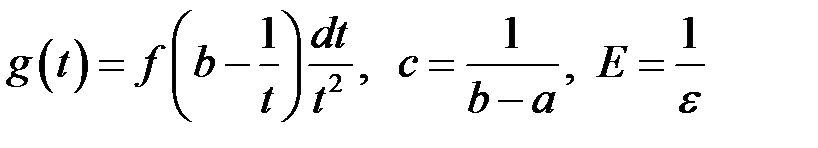 .
.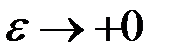 , то очевидно
, то очевидно 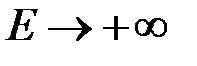 , і ми отримуємо:
, і ми отримуємо: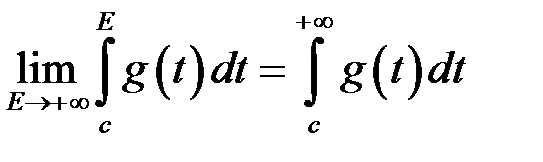 .
.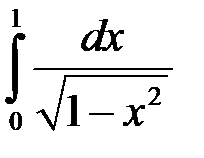 .
.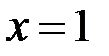 . Маємо:
. Маємо: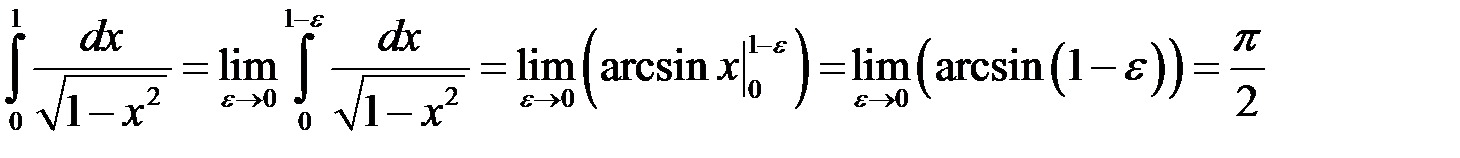 .
.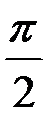 .
.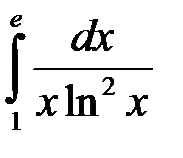 .
.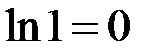 . Маємо:
. Маємо: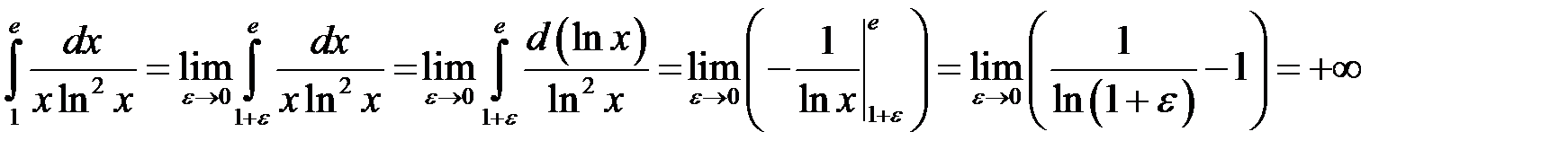
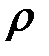 інтеграл збігається, а дл яких розбігається:
інтеграл збігається, а дл яких розбігається: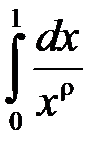 .
.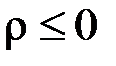 , то інтеграл не є невласним, оскільки підінтегральна функція
, то інтеграл не є невласним, оскільки підінтегральна функція 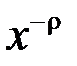 буде обмеженою на відрізку
буде обмеженою на відрізку 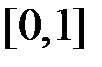 . Отже залишилось дослідити випадок
. Отже залишилось дослідити випадок 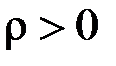 . Тоді особливою точкою буде точка
. Тоді особливою точкою буде точка 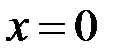 . Нехай спочатку
. Нехай спочатку 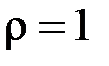 . Маємо:
. Маємо: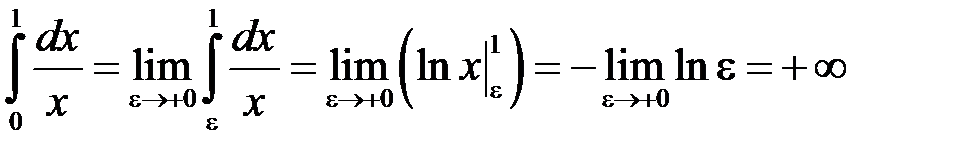 , отже інтеграл розбіжний. Нехай тепер
, отже інтеграл розбіжний. Нехай тепер 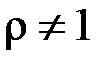 . Тоді:
. Тоді: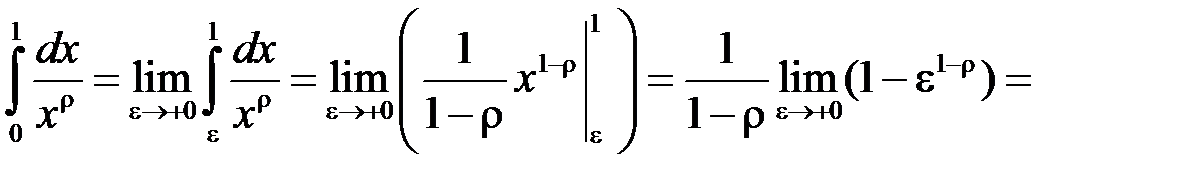
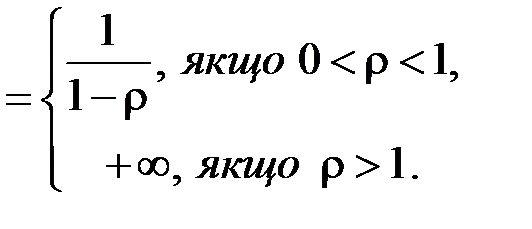
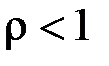 , і розбігається, якщо
, і розбігається, якщо 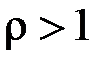 .
.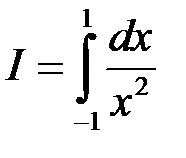 .
.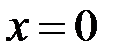 , яка належить інтервалу
, яка належить інтервалу 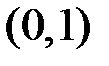 . Розіб’ємо цей інтеграл на два інтеграли
. Розіб’ємо цей інтеграл на два інтеграли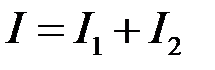 , де
, де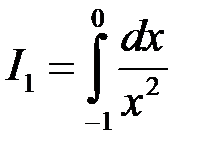 ,
, 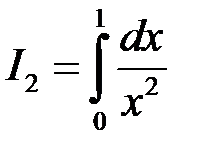 .
. розбіжний, то розбіжним буде й інтеграл
розбіжний, то розбіжним буде й інтеграл 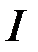 . Таким чином про його обчислення взагалі не може йти мова.
. Таким чином про його обчислення взагалі не може йти мова.