Поняття визначеного інтеграла Рімана, як ми бачили, має зміст для скінченного проміжку і для обмеженої на цьому проміжку функції. Якщо хоч би одна з цих умов не виконана, то інтеграла у власному розумінні не існує. Тому виникає необхідність поширити поняття інтеграла на випадки нескінченного проміжку та необмеженої функції. Відповідно виникають інші поняття – так званих невласних інтегралів I роду (у випадку нескінченного проміжку) та II роду (у випадку необмеженої на проміжку функції). Ми почнемо з поняття невласного інтеграла I роду.
Нехай функція 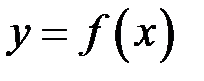 визначена на проміжку
визначена на проміжку 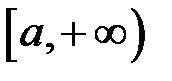 і інтегровна на будь якому відрізку
і інтегровна на будь якому відрізку 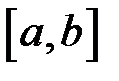 , де
, де 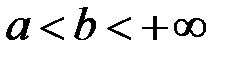 .
.
Означення.Невласним інтегралом I роду від функції 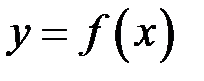 на проміжку
на проміжку 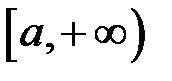 називається границя
називається границя
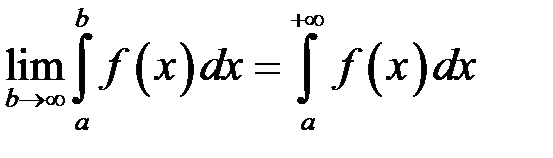 . (8.1)
. (8.1)
Якщо ця границя існує та скінченна, інтеграл (8.1) називається збіжним, у протилежному випадку – розбіжним.
Таким чином невласний інтеграл I роду не є границею інтегральних сум, а є границею визначеного інтеграла зі змінною верхньою межею. З геометричної точки зору він виражає площу необмеженої області (рис. 5).
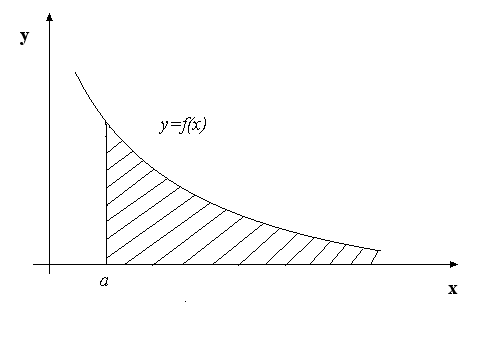
Рис. 5.
Аналогічно означається невласний інтеграл I роду на проміжку 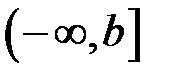 :
:
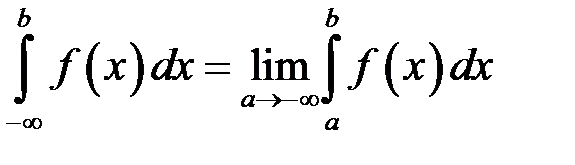 (8.2)
(8.2)
А також можливі невласні інтеграли з обома нескінченними межами:
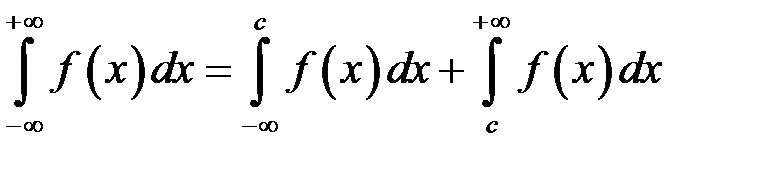 , (8.3) де
, (8.3) де 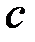 – довільне число. Інтеграл у лівій частині формули (8.3) збігається тоді і тільки тоді, коли незалежно один від одного збігаються обидва інтеграли у правій частині цієї формули.
– довільне число. Інтеграл у лівій частині формули (8.3) збігається тоді і тільки тоді, коли незалежно один від одного збігаються обидва інтеграли у правій частині цієї формули.
Приклади.
1. Дослідити на збіжність та у випадку збіжності обчислити інтеграл?
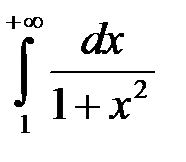 .
.
Маємо:
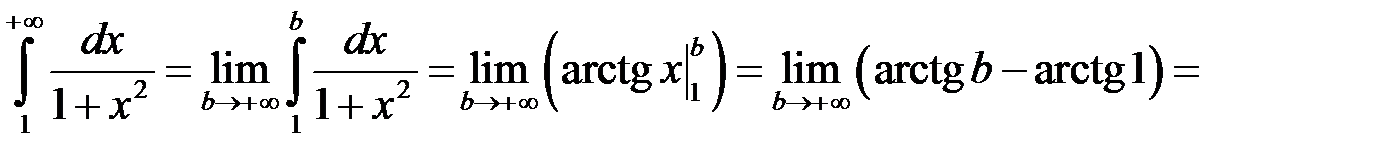
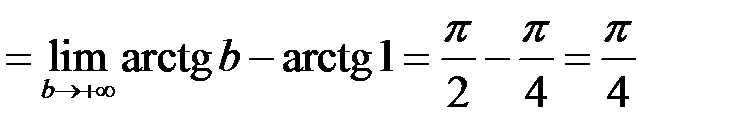 .
.
Отже інтеграл збіжний, і його значення дорівнює 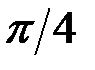 .
.
2. Дослідити на збіжність інтеграл
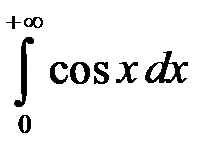 .
.
Маємо:
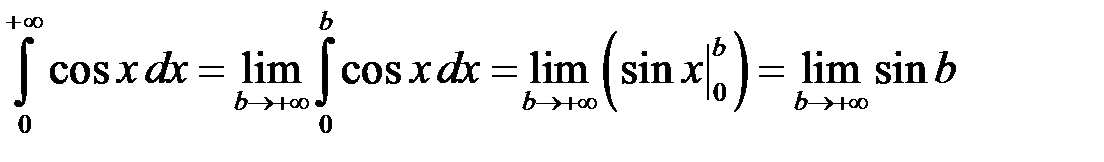 .
.
Відомо, що функція 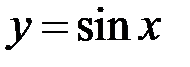 не має границі при
не має границі при 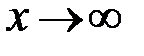 . Отже даний інтеграл розбіжний.
. Отже даний інтеграл розбіжний.
3. Дослідити на збіжність інтеграл
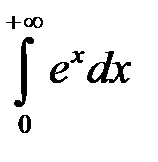 .
.
Маємо:
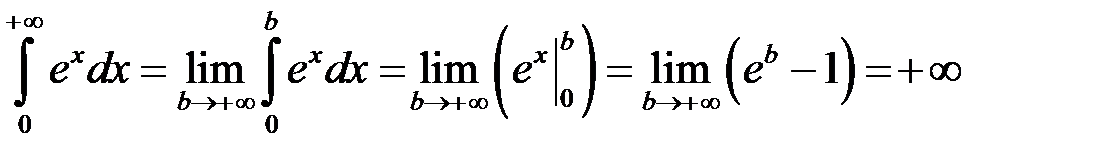 .
.
Отже даний інтеграл розбіжний (границя існує, але вона нескінченна).
4. 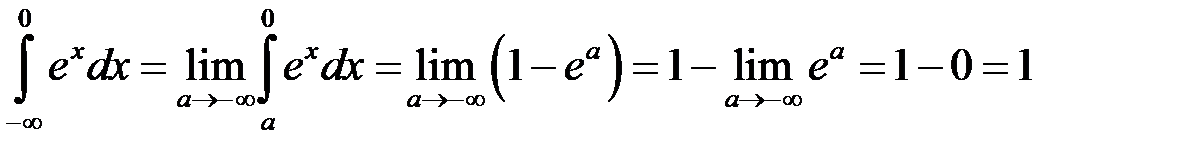 .
.
Даний інтеграл збіжний, і його значення дорівнює 1.
5. Визначимо, для яких значень параметра 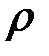 збігається інтеграл:
збігається інтеграл:
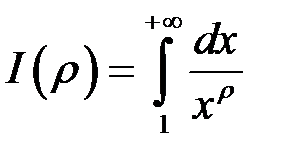 .
.
У випадку 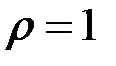 маємо:
маємо:
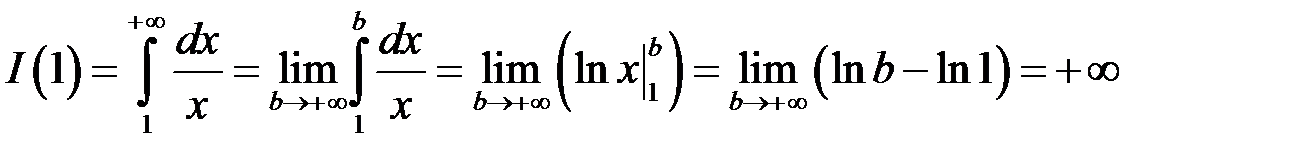 , тобто інтеграл розбіжний.
, тобто інтеграл розбіжний.
Якщо 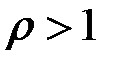 , то
, то
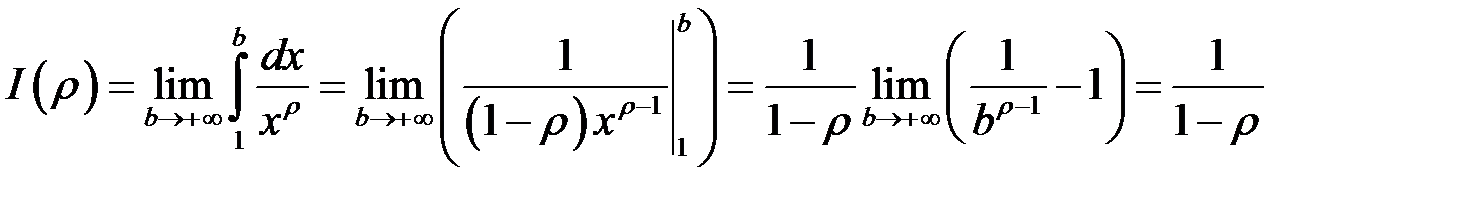 , отже інтеграл збіжний.
, отже інтеграл збіжний.
Якщо 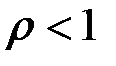 , то
, то
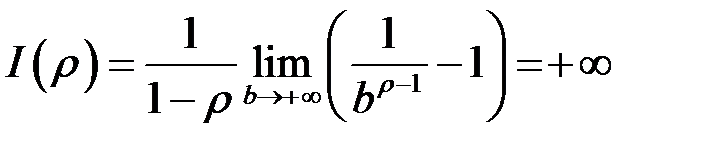 , і інтеграл розбіжний. Таким чином
, і інтеграл розбіжний. Таким чином 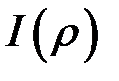 є збіжним, коли
є збіжним, коли 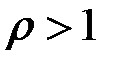 , і розбіжним, коли
, і розбіжним, коли 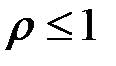 .
.


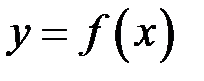 визначена на проміжку
визначена на проміжку 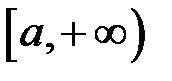 і інтегровна на будь якому відрізку
і інтегровна на будь якому відрізку 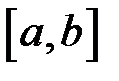 , де
, де 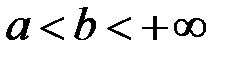 .
.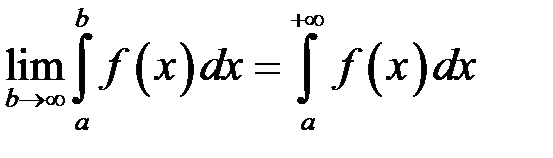 . (8.1)
. (8.1)
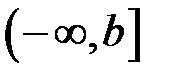 :
: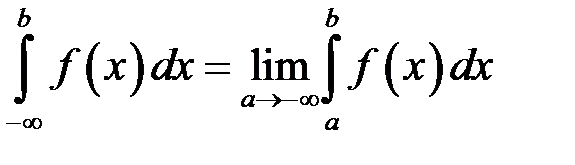 (8.2)
(8.2)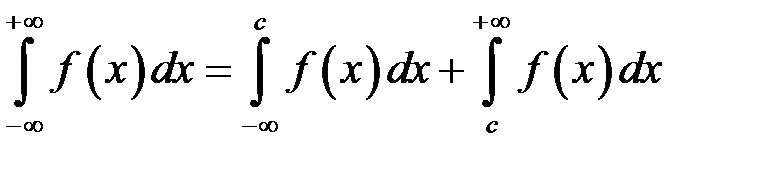 , (8.3) де
, (8.3) де 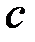 – довільне число. Інтеграл у лівій частині формули (8.3) збігається тоді і тільки тоді, коли незалежно один від одного збігаються обидва інтеграли у правій частині цієї формули.
– довільне число. Інтеграл у лівій частині формули (8.3) збігається тоді і тільки тоді, коли незалежно один від одного збігаються обидва інтеграли у правій частині цієї формули.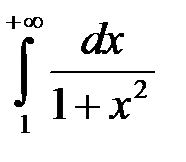 .
.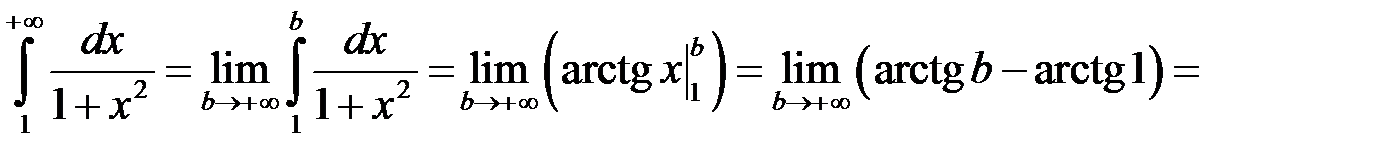
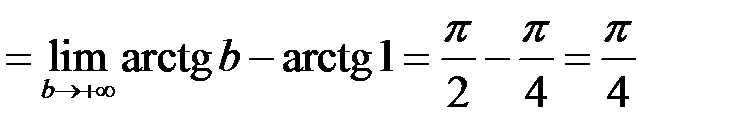 .
.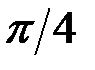 .
.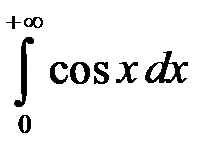 .
.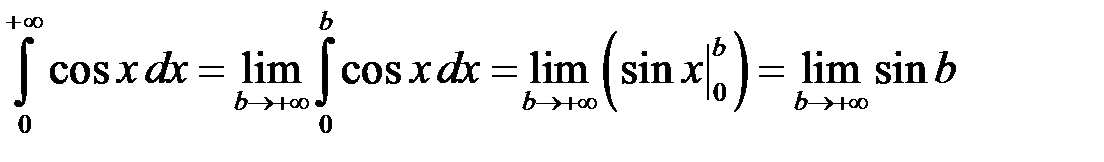 .
.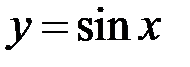 не має границі при
не має границі при 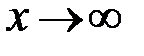 . Отже даний інтеграл розбіжний.
. Отже даний інтеграл розбіжний.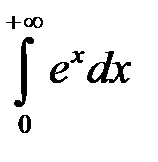 .
.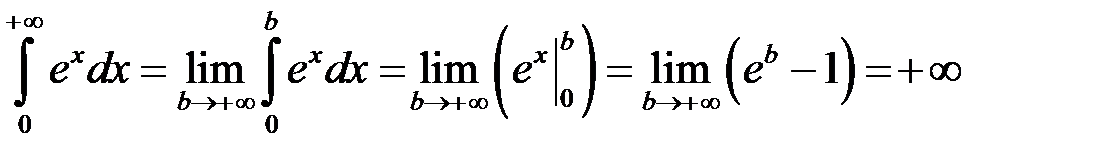 .
.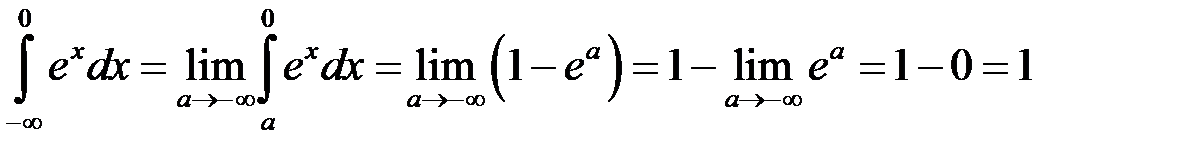 .
.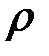 збігається інтеграл:
збігається інтеграл: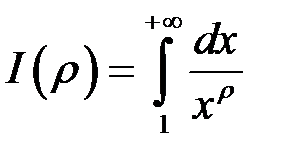 .
.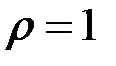 маємо:
маємо: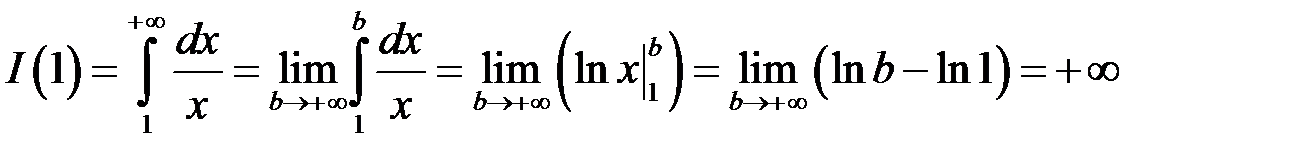 , тобто інтеграл розбіжний.
, тобто інтеграл розбіжний.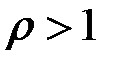 , то
, то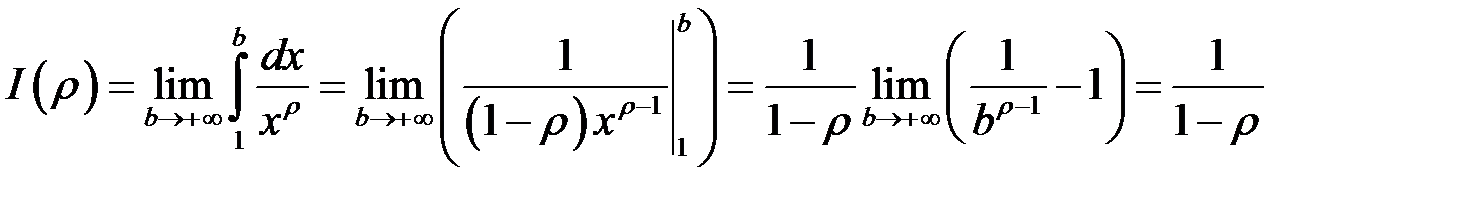 , отже інтеграл збіжний.
, отже інтеграл збіжний.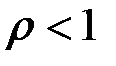 , то
, то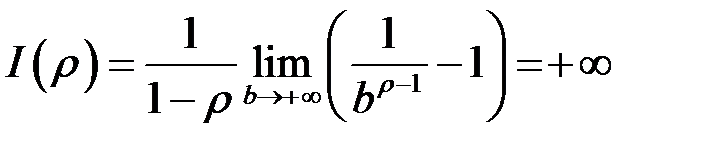 , і інтеграл розбіжний. Таким чином
, і інтеграл розбіжний. Таким чином 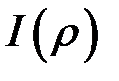 є збіжним, коли
є збіжним, коли 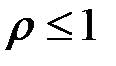 .
.