Знайти екстремум функції
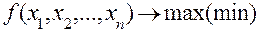
при обмеженнях
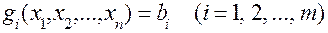
де обмеження складаються лише із рівнянь, відсутні умови невід’ємності, функції  і
і  неперервні разом із своїми частинними похідними.
неперервні разом із своїми частинними похідними.
Така задача називається задачею на умовний екстремум або класичною задачею оптимізації.
Основна ідея метода множників Лагранжа полягає в переході від задачі на умовний екстремум до задачі знаходження безумовного екстремуму деякої спеціальним чином побудованої функції Лагранжа.
Складаємо функцію Лагранжа:
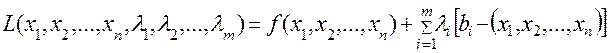 ,
,
де  - множники Лагранжа, кількість яких дорівнює числу обмежень.
- множники Лагранжа, кількість яких дорівнює числу обмежень.
Приклад. Необхідно використовуючи метод множників Лагранжа визначити екстремум функції:

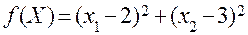
при обмеженнях x1 +x2 = 7.
Розв’язання. Складемо функцію Лагранжа. Оскільки за умовою тільки одно обмеження, то множник Лагранжа буде один  .
.
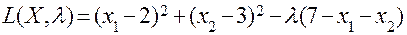 .
.
Знайдемо частинні похідні по 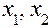 і
і  :
:

Прирівнюючи похідні до нуля, отримаємо систему рівнянь для визначення стаціонарних точок:

Розв’язавши цю систему рівнянь знаходимо 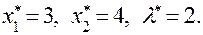 Отже, отримали стаціонарну точку x* =(3, 4, 2).. Перевіримо достатню умову екстремуму в цій точці. Для цього знаходимо другі похідні і обчислюємо матрицю Гессе:
Отже, отримали стаціонарну точку x* =(3, 4, 2).. Перевіримо достатню умову екстремуму в цій точці. Для цього знаходимо другі похідні і обчислюємо матрицю Гессе:
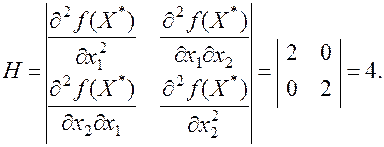 Оскільки матриця Гессе H додатне визначена, а головний мінор першого порядку
Оскільки матриця Гессе H додатне визначена, а головний мінор першого порядку 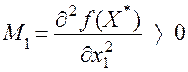 і мінор другого порядку
і мінор другого порядку 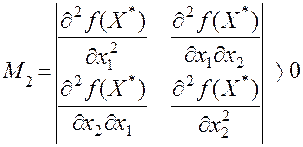 ,
,
то функція f(x) опукла і в точці x* має абсолютний мінімум 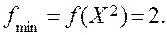
Можна відмітити, що такий же результат отримаємо, якщо дослідження задачі на умовний екстремум функції f(x) зведемо к дослідженню на безумовний екстремум функції f1(x), отриманої шляхом перетворення функції f(x). Для цього з рівняння 7-х1-х2 = 0 знайдемо x1 = 7 –x2 і підставимо його в функціонал. В результаті отримаємо функцію однієї змінної x2: 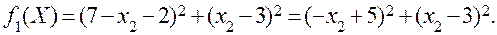
Знайдемо стаціонарну точку цієї функції
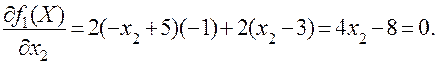
Маємо стаціонарну точку 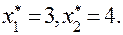 По аналогії із вище наведеним прикладом встановлюємо, що точка x* - є точкою мінімуму і функція f(x) в цій точці приймає мінімальне значення.
По аналогії із вище наведеним прикладом встановлюємо, що точка x* - є точкою мінімуму і функція f(x) в цій точці приймає мінімальне значення.


 і
і  неперервні разом із своїми частинними похідними.
неперервні разом із своїми частинними похідними.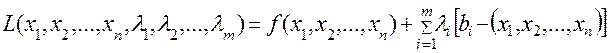 ,
, - множники Лагранжа, кількість яких дорівнює числу обмежень.
- множники Лагранжа, кількість яких дорівнює числу обмежень.
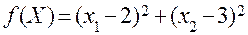
 .
.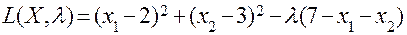 .
. і
і 

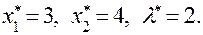 Отже, отримали стаціонарну точку x* =(3, 4, 2).. Перевіримо достатню умову екстремуму в цій точці. Для цього знаходимо другі похідні і обчислюємо матрицю Гессе:
Отже, отримали стаціонарну точку x* =(3, 4, 2).. Перевіримо достатню умову екстремуму в цій точці. Для цього знаходимо другі похідні і обчислюємо матрицю Гессе: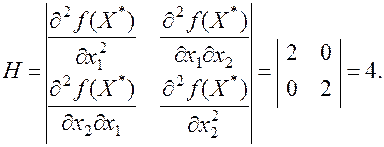 Оскільки матриця Гессе H додатне визначена, а головний мінор першого порядку
Оскільки матриця Гессе H додатне визначена, а головний мінор першого порядку 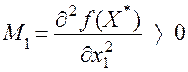 і мінор другого порядку
і мінор другого порядку 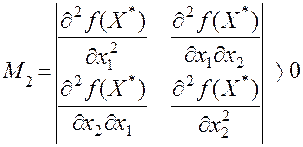 ,
,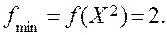
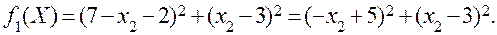
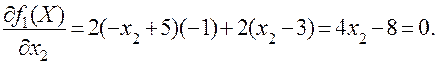
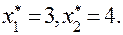 По аналогії із вище наведеним прикладом встановлюємо, що точка x* - є точкою мінімуму і функція f(x) в цій точці приймає мінімальне значення.
По аналогії із вище наведеним прикладом встановлюємо, що точка x* - є точкою мінімуму і функція f(x) в цій точці приймає мінімальне значення.