Алгоритм розв’язання задачі квадратичного програмування:
1. Складаємо функцію Лагранжа.
2. Записуємо необхідні і достатні умови існування сідлової точки функції Лагранжа .
3. Використовуючи метод штучного базису, або встановлюємо, що сідлова точка функції Лагранжа відсутня, або знаходимо її координати.
4. Записуємо оптимальний розв’язок задачі квадратичного програмування і знаходимо значення цільової функції.
Приклад.Знайти максимальне значення функції
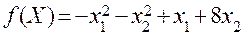 (6.3.1)
(6.3.1)
при обмеженнях
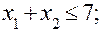 (6.3.2)
(6.3.2)

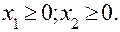 (6.3.3)
(6.3.3)
Розв’язання. Функція 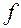 є угнутою оскільки являє собою суму лінійної функції f1 = x1 +8 x2 (яку також можна розглядати як угнуту) і квадратичної форми f2 = -x12 – x22, яка є недодатне визначеною і йому також є угнутою функцією. Система обмежень задачі містить лише лінійні рівняння. Отже, можна застосувати теорему Куна-Таккера. З цією метою запишемо функцію Лагранжа:
є угнутою оскільки являє собою суму лінійної функції f1 = x1 +8 x2 (яку також можна розглядати як угнуту) і квадратичної форми f2 = -x12 – x22, яка є недодатне визначеною і йому також є угнутою функцією. Система обмежень задачі містить лише лінійні рівняння. Отже, можна застосувати теорему Куна-Таккера. З цією метою запишемо функцію Лагранжа:
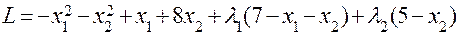 (6.3.4)
(6.3.4)
Запишемо необхідні і достатні умови існування сідлової точки побудованої функції Лагранжа:
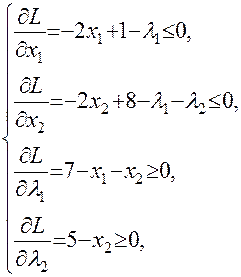 (6.3.5)
(6.3.5)
 (6.3.6)
(6.3.6)
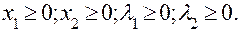 (6.3.7)
(6.3.7)
Запишемо систему (6.3.5) таким чином:
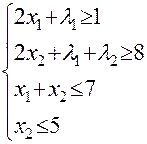 (6.3.8)
(6.3.8)
Зведемо ці нерівності до строгих рівностей. З цією метою введемо додаткові невід’ємні змінні 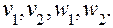
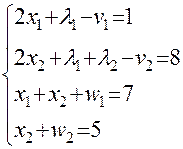 (6.3.9)
(6.3.9) 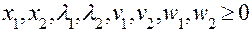 (6.3.10)
(6.3.10)
Враховуючи рівності (6.3.9) можна записати:
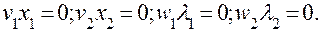 (6.3.11)
(6.3.11)
Для знаходження базисного розв’язку системи лінійних рівнянь (6.3.9) застосовуємо метод штучного базису. Для цього в перше і друге рівняння системи (6.3.9) вводимо додаткові невід’ємні змінні z1 , z2 і розв’яжемо задачу лінійного програмування:
 (6.3.12)
(6.3.12)
при обмеженнях
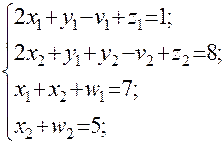 (6.3.13)
(6.3.13)
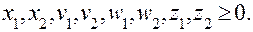 (6.3.14)
(6.3.14)
Розв’язавши задачу (6.3.12) - (6.3.13) знаходимо допустимий розв’язок системи лінійних рівнянь (6.3.13) (табл.1).
Як видно з таблиці 1 розв’язком задачі є
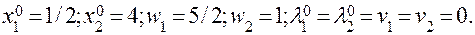
Оскільки 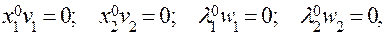 то (x0 , λ0 ) = (1/2, 4, 0, 0) є сідловою точкою функції Лагранжа задачі (6.3.1)-(6.3.3). Отже, x* = (1/2; 4) оптимальний план задачі і fmax = 16,75.
то (x0 , λ0 ) = (1/2, 4, 0, 0) є сідловою точкою функції Лагранжа задачі (6.3.1)-(6.3.3). Отже, x* = (1/2; 4) оптимальний план задачі і fmax = 16,75.
Таблиця1.
| і
| Б
| Сб
| А0
|
|
|
|
|
|
|
|
| -М
| -М
|
| Ах1
| Ах2
| Аλ1
| Аλ2
| Аν1
| Аν2
| Аω1
| Аω2
| Аz1
| Az2
|
 1 1
| Az1
| -M
|
|
|
|
|
| -1
|
|
|
|
|
|
|
| Az2
| -M
|
|
|
|
|
|
| -1
|
|
|
|
|
|
| Aw1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Aw2
|
|
|
|
|
|
|
|
|
|
|
|
|
| m+1
|
|
|
|  0 0
|  0 0
|
|
|
|
|
|
|
|
|
| m+2
|
|
| -9
| -2
| -2
| -2
| -1
|
|
|
|
|
|
|
|
| Ax1
|
| 1/2
|
|
| 1/2
|
| -1/2
|
|
|
| 1/2
|
|
 2 2
| Az2
| -M
|
|
|
|
|
|
| -1
|
|
|
|
|
|
| Aw1
|
| 13/2
|
|
| -1/2
|
| 1/2
|
|
|
| -1/2
|
|
|
| Aw2
|
|
|
|
|
|
|
|
|
|
|
|
|
| m+1
|
|
|
|
|  0 0
|
|
|
|
|
|
|
|
|
| m+2
|
|
| -8
|
| -2
| -1
| -1
|
|
|
|
|
|
|
|
| Ax1
|
| 1/2
|
|
| 1/2
|
| -1/2
|
|
|
|
|
|
|
| Ax2
|
|
|
|
| 1/2
| 1/2
|
| -1/2
|
|
|
|
|
|
| Aw1
|
| 5/2
|
|
| 1/2
| -1/2
| 1/2
| 1/2
|
|
|
|
|
|
| Aw2
|
|
|
|
| -1/2
| -1/2
|
| 1/2
|
|
|
|
|
| m+1
|
|
|
|
|
|
|
|
|
|
|  0 0
|
|
|
7. Рекомендована література


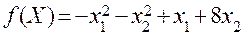 (6.3.1)
(6.3.1)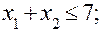 (6.3.2)
(6.3.2)
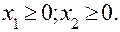 (6.3.3)
(6.3.3)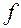 є угнутою оскільки являє собою суму лінійної функції f1 = x1 +8 x2 (яку також можна розглядати як угнуту) і квадратичної форми f2 = -x12 – x22, яка є недодатне визначеною і йому також є угнутою функцією. Система обмежень задачі містить лише лінійні рівняння. Отже, можна застосувати теорему Куна-Таккера. З цією метою запишемо функцію Лагранжа:
є угнутою оскільки являє собою суму лінійної функції f1 = x1 +8 x2 (яку також можна розглядати як угнуту) і квадратичної форми f2 = -x12 – x22, яка є недодатне визначеною і йому також є угнутою функцією. Система обмежень задачі містить лише лінійні рівняння. Отже, можна застосувати теорему Куна-Таккера. З цією метою запишемо функцію Лагранжа: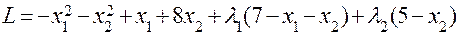 (6.3.4)
(6.3.4)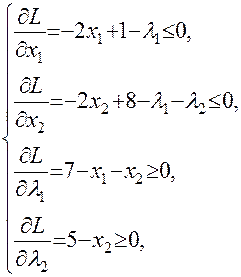 (6.3.5)
(6.3.5) (6.3.6)
(6.3.6)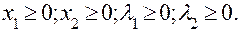 (6.3.7)
(6.3.7)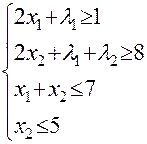 (6.3.8)
(6.3.8)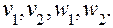
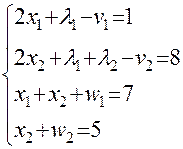 (6.3.9)
(6.3.9) 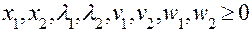 (6.3.10)
(6.3.10)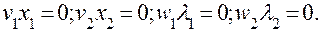 (6.3.11)
(6.3.11) (6.3.12)
(6.3.12)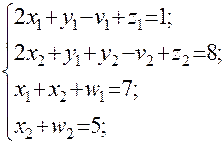 (6.3.13)
(6.3.13)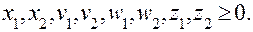 (6.3.14)
(6.3.14)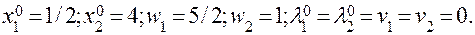
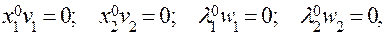 то (x0 , λ0 ) = (1/2, 4, 0, 0) є сідловою точкою функції Лагранжа задачі (6.3.1)-(6.3.3). Отже, x* = (1/2; 4) оптимальний план задачі і fmax = 16,75.
то (x0 , λ0 ) = (1/2, 4, 0, 0) є сідловою точкою функції Лагранжа задачі (6.3.1)-(6.3.3). Отже, x* = (1/2; 4) оптимальний план задачі і fmax = 16,75. 1
1
 0
0
 0
0
 0
0
 0
0