Геометричні образи квадратичного рівняння у канонічній формі можна представити у вигляді ізоліній при кількості факторів к=2 та у вигляді ізоповерхонь при кількості факторів к=3.
У випадку коли к=2 загальний вигляд рівняння буде
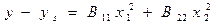
1. Обидва коеф В11 і В22 мають однакові знаки
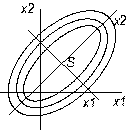 Центр еліпсів S є max якщо коеф додатні, якщо В22 за абсолютною величиною менше ніж В11 то еліпси вздовж осі х2 і навпаки
Центр еліпсів S є max якщо коеф додатні, якщо В22 за абсолютною величиною менше ніж В11 то еліпси вздовж осі х2 і навпаки
Повехня відгуку є еліптичний параболоїд. В цьому випадку для пошуку екстремума достатньо поставити експеримент в центрі фігури S та перевірити наскільки добре значення параметру оптимізації співпадає з експерементом.
2. Коеф В11 і В22 мають різні знаки
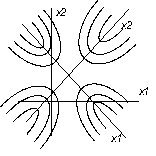 Гіперболи витягнуті по тій осі, якій відповідає менше за абсолютною величиною значення коеф канонічному рівнянні. В цьому випадку значення параметру оптимізації збільшується якщо рухатись з центру фігури по цій осі та зменшується при русі по іншій.
Гіперболи витягнуті по тій осі, якій відповідає менше за абсолютною величиною значення коеф канонічному рівнянні. В цьому випадку значення параметру оптимізації збільшується якщо рухатись з центру фігури по цій осі та зменшується при русі по іншій.
Поверхня відгуку є гіперболічній параболоїд. Дослідник вибирає напрямок руху в залежності від того що його цікавить max або min . Тут як і при крутому сходженні намічається серія уявних експертів частина з яких реалізується.
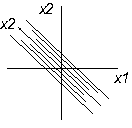 3.Один з коеф канонічного рівняння =0. При цьому не має одного центру з max значенням параметру оптимізації. При визначенні центру підходить будь-яка точка на осі відповідно незначущого коєфіцієнту канонічного рівняння. Поверхня відгуку є стаціонарним піднесенням.
3.Один з коеф канонічного рівняння =0. При цьому не має одного центру з max значенням параметру оптимізації. При визначенні центру підходить будь-яка точка на осі відповідно незначущого коєфіцієнту канонічного рівняння. Поверхня відгуку є стаціонарним піднесенням.
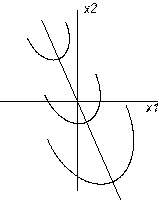 4.Один з коеф =0. При цьому ценрт фігури знаходиться у нескінченності. Поверхня відгуку є зростаюче піднесення-гребень. В цьому випадку розташовують поч. координат в будь-якій точці (частіше всього близ центру експеременту) на осі яка відповідає не значущому коеф канонічного рівняння.
4.Один з коеф =0. При цьому ценрт фігури знаходиться у нескінченності. Поверхня відгуку є зростаюче піднесення-гребень. В цьому випадку розташовують поч. координат в будь-якій точці (частіше всього близ центру експеременту) на осі яка відповідає не значущому коеф канонічного рівняння.
Якщо кількість факторів к=3, то рівняння буде: 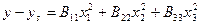
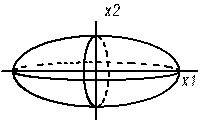
1.Всі коеф Віі мають однакові знаки. Поверхня відгуку є еліпсоїд обертаня та має екстремум в центрі еліпсоїда.
2.Якщо знак одного з коєфіцієнтів протилежний знаку двох інших, то має місце одно- або двопорожнинний гіпербалоїд.
3. Якщо один з коеф канонічного рівняння наближається до 0, то поверхня відгуку може бути еліптичним циліндром, якщо 2 коеф мають однакові знаки;
або гіперболічним циліндром, якщо знаки коеф різні.
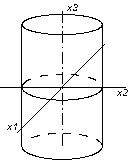
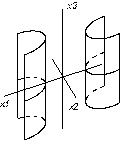
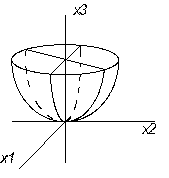
 4.Також якщо два з коеф наближаються до 0, то поверхня відгуку може бути еліптичним обо гіперболічним пораболоїдом.
4.Також якщо два з коеф наближаються до 0, то поверхня відгуку може бути еліптичним обо гіперболічним пораболоїдом.
 5.Якщо 2 коеф канонічного рівняння =0, то поверхня відгуку може бути серією паралельно площини або параболічний циліндр.
5.Якщо 2 коеф канонічного рівняння =0, то поверхня відгуку може бути серією паралельно площини або параболічний циліндр.
Симплексний метод планування експерименту
Суть методу: у випадку коли нема необхідності у математичній моделі досліджуємого процесу, а потрібно відшукати ділянку оптимума використовують так званий сімплексний метод планування експеременту.
Принцип симплексного планування полягає в тому, що умовам першої серії експерементів відповідають крд точок які утворюють правильний симплекс (багатогранник). Правильний симплекс утворюють к+1 точки які розташовані на одинаковій відстані одна від одної у к вимірному просторі, де к кількість факторів. В одновимірному просторі симплекс буде частиною прямої, для двох факторів – рівностороній трикутник, при трьох факторах тетраедр. Потім цей симплекс деяким чином переміщується (кантується) по поверхні відгуку.
Кантування симплекса по поверхні відгуку здійснюється по такій послідовності.
– з експерементів першої серії, тобто з вершини правильного симплекса вибирається точка з найгіршим результатом далі визначають крд нової точки яка є дзеркальним відображенням точки з найгіршим результатом відносно протилежної грані симплекса. При цьому утворюється новий симплекс. В цій новій точці ставлять експеремент. Результати нового симплекса знову порівнюють. Вибирають точку з найгіршим результатом і т.д.
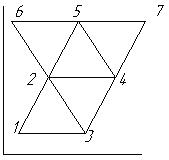 Якщо в результаті кантування сиплекса одржали найгірший результат то рухатись в цьому напрямку немає сенсу. Можна спробувати рухатись відносно нової точки з найгіршим результатом. Кантування продовжується до тих пір поки в наступній точці знову буде отримано найгірший результат.
Якщо в результаті кантування сиплекса одржали найгірший результат то рухатись в цьому напрямку немає сенсу. Можна спробувати рухатись відносно нової точки з найгіршим результатом. Кантування продовжується до тих пір поки в наступній точці знову буде отримано найгірший результат.


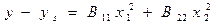
 Центр еліпсів S є max якщо коеф додатні, якщо В22 за абсолютною величиною менше ніж В11 то еліпси вздовж осі х2 і навпаки
Центр еліпсів S є max якщо коеф додатні, якщо В22 за абсолютною величиною менше ніж В11 то еліпси вздовж осі х2 і навпаки Гіперболи витягнуті по тій осі, якій відповідає менше за абсолютною величиною значення коеф канонічному рівнянні. В цьому випадку значення параметру оптимізації збільшується якщо рухатись з центру фігури по цій осі та зменшується при русі по іншій.
Гіперболи витягнуті по тій осі, якій відповідає менше за абсолютною величиною значення коеф канонічному рівнянні. В цьому випадку значення параметру оптимізації збільшується якщо рухатись з центру фігури по цій осі та зменшується при русі по іншій.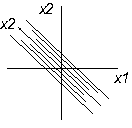 3.Один з коеф канонічного рівняння =0. При цьому не має одного центру з max значенням параметру оптимізації. При визначенні центру підходить будь-яка точка на осі відповідно незначущого коєфіцієнту канонічного рівняння. Поверхня відгуку є стаціонарним піднесенням.
3.Один з коеф канонічного рівняння =0. При цьому не має одного центру з max значенням параметру оптимізації. При визначенні центру підходить будь-яка точка на осі відповідно незначущого коєфіцієнту канонічного рівняння. Поверхня відгуку є стаціонарним піднесенням.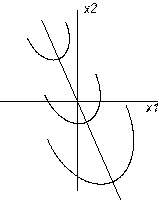 4.Один з коеф =0. При цьому ценрт фігури знаходиться у нескінченності. Поверхня відгуку є зростаюче піднесення-гребень. В цьому випадку розташовують поч. координат в будь-якій точці (частіше всього близ центру експеременту) на осі яка відповідає не значущому коеф канонічного рівняння.
4.Один з коеф =0. При цьому ценрт фігури знаходиться у нескінченності. Поверхня відгуку є зростаюче піднесення-гребень. В цьому випадку розташовують поч. координат в будь-якій точці (частіше всього близ центру експеременту) на осі яка відповідає не значущому коеф канонічного рівняння.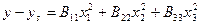

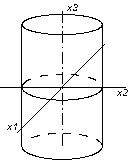


 4.Також якщо два з коеф наближаються до 0, то поверхня відгуку може бути еліптичним обо гіперболічним пораболоїдом.
4.Також якщо два з коеф наближаються до 0, то поверхня відгуку може бути еліптичним обо гіперболічним пораболоїдом. 5.Якщо 2 коеф канонічного рівняння =0, то поверхня відгуку може бути серією паралельно площини або параболічний циліндр.
5.Якщо 2 коеф канонічного рівняння =0, то поверхня відгуку може бути серією паралельно площини або параболічний циліндр. Якщо в результаті кантування сиплекса одржали найгірший результат то рухатись в цьому напрямку немає сенсу. Можна спробувати рухатись відносно нової точки з найгіршим результатом. Кантування продовжується до тих пір поки в наступній точці знову буде отримано найгірший результат.
Якщо в результаті кантування сиплекса одржали найгірший результат то рухатись в цьому напрямку немає сенсу. Можна спробувати рухатись відносно нової точки з найгіршим результатом. Кантування продовжується до тих пір поки в наступній точці знову буде отримано найгірший результат.