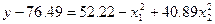Канонічне перетворення рівняння полягає у виборі нової системи координат в якій рівняння приймає настільки простий вигляд, що геометрична характеристика його не викликає труднощів. Такого роду перетвотення зводиться до паралельного переносу (при цьому в початковому рівнянні зникають і 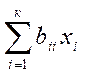 ) та до повороту координатних осей (при цьому зникають ефекти взаємодій
) та до повороту координатних осей (при цьому зникають ефекти взаємодій 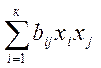 )
)
Квадратне рівняння в канонічній формі має вигляд 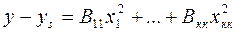
де у – значення параметра оптимізації в новому центрі
Вкк – значення коефіціента регресії в канонічній формі
Для паралельного переносу початкове рівняння диференціюють по кожній з зазначених змінних та прирівнюють частинні похідні до 0. Вирішуючи систему рівнянь можна знайти координати нового центру S в старих осях координат. Підставляючи ці нові крд в початкове рівняння визначають величину параметру оптимізації в новому центрі ys.
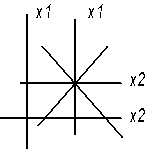
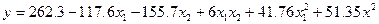
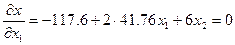
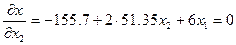
x1s=1.3 x2s=1.44 → ys=77.49
Після переносу системи крд в новий центр здійснюють поворот крд на деякий кут. З метою вирішують таке хар-не р-ня.
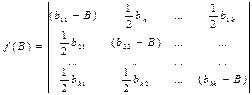
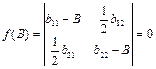
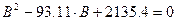 В11=52,22 В22=40,89
В11=52,22 В22=40,89 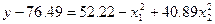
Канонічна форма зручна для аналізу та оптимізації. Якщо всі коефіцієнти в≠0 та центр поверхні S лежить на ділянці експерименту то можливі такі випадки.
Всі коеф Bі < 0 тоді рух в будь-якому напрямку від центру тільки зменшує параметр оптимізації. Всі Ві > 0 тоді рух в будь-якому напрямку від центру тільки збільшує параметр оптимізації. Частина Ві > 0 і частина Ві < 0
Тоді для збільшення параметру оптимізації треба здійснювати рух з центру таким чином щоб значення хі для коеф з від’ємним знаком = 0 тобто шукати екстремум уздовж осей з Віі > 0. І навпаки для зменшення параметру оптимізації треба рухатись вздовж осей з Віі< 0.


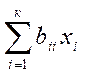 ) та до повороту координатних осей (при цьому зникають ефекти взаємодій
) та до повороту координатних осей (при цьому зникають ефекти взаємодій 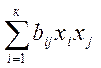 )
)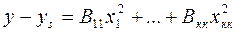
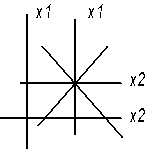
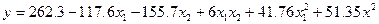
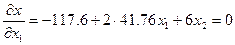
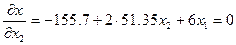
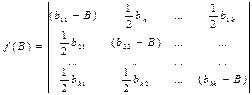
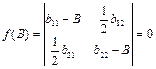
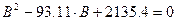 В11=52,22 В22=40,89
В11=52,22 В22=40,89