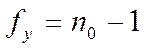Щоб виключити вплив систематичних помилок, які викликані зовнішніми умовами, рекомендується випадкова послідовність при постановці експерименту, яка запланована матрицею.
Експеримент рандомізувати за часу .
Наприклад: проводиться експеримент для матриці 23 , при цьому кожний експеримент дублюється два рази. В літературі по математичній статистиці є таблиці випадкових чисел.
19.Визначення коефіцієнтів моделі типу 22 та перевірка їх значимості.
В загальному випадку для будь-якої кількості коефіцієнтів моделі розраховують за формулою: 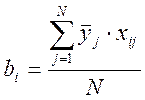 і – номер фактора (0,1,2...к);
і – номер фактора (0,1,2...к);
j – номер експерименту; 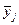 – середнє арифметичне значення параметру оптимізації в j – експерименті;
– середнє арифметичне значення параметру оптимізації в j – експерименті; 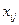 – кодове значення (±1) фактора і або ефекту взаємодії факторів у j-му експерименті.
– кодове значення (±1) фактора і або ефекту взаємодії факторів у j-му експерименті.
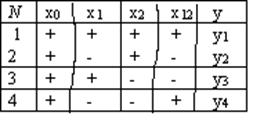
b0= (y1(+1)+ y2(+1) +y3(+1)+y4(+1))/4,
b1= (y1-y2+y3-y4)/4 і т.д.
Перевірка значимості коефіцієнтів проводиться незалежно для кожного експерименту.
Спочатку розраховують “довірчий інтервал” Δbi = ti · Sbi , де ti – табличне значення критерію Стьюдента для вибраного рівня значимості та кількості ступенів свободи з якою визначалась дисперсія; Sbi – квадратична помилка і-го коефіцієнта, яка розраховується за формулою:  Sbi2 –дисперсія і-го коефіцієнта, яка знаходиться за формулою
Sbi2 –дисперсія і-го коефіцієнта, яка знаходиться за формулою
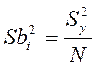
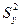 – дисперсія параметра оптимізації.
– дисперсія параметра оптимізації.
Коефіцієнт моделі вважають значимим, якщо його абсолютна величина більше довірчого інтервалу. 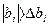 Статистично не значимі коефіцієнти можуть бути виключені з рівняння моделі.
Статистично не значимі коефіцієнти можуть бути виключені з рівняння моделі.
20. Перевірка адекватності моделі типу 22
Перевірка адекватності здійснюється за критерієм Фішера
Fp = Sад2/S2y
Sад2- дисперсія адекватності зі своєю кількістю свободи; fад = f1
S2y – дисперсія параметру оптимізації зі своєю кількістю свободи fу = f2
Модель вважається адекватною з відповідною довірчою вірогідністю та кількістю ступенів свободи, якщо Fр<Fт , де Fт – табличне значення критерію Фішера.
Кількість ступенів свободи для Sад2 дорівнює кількості експериментів, які відрізняються один від одного і результат яких використовується для підрахування коефіцієнтів моделі мінус кількість значимих коефіцієнтів.
Кількість ступенів свободи для S2y:
1. Якщо нерівномірне дублювання: 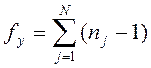 , де N– кількість експериментів у матриці планування; j – номер експерименту або точка матриці планування; n – кількість паралельних експериментів в ј-ій точці матриці планування.
, де N– кількість експериментів у матриці планування; j – номер експерименту або точка матриці планування; n – кількість паралельних експериментів в ј-ій точці матриці планування.
2. Якщо рівномірне дублювання: 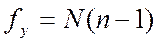 , n – однакова для всіх рядків матриці планування кількість паралельних експериментів.
, n – однакова для всіх рядків матриці планування кількість паралельних експериментів.
3. У випадку коли паралельні експерименти проводяться в нульовій точці.
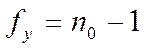
де n0-кількість паралельних експериментів в 0 точці.


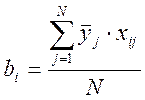 і – номер фактора (0,1,2...к);
і – номер фактора (0,1,2...к);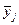 – середнє арифметичне значення параметру оптимізації в j – експерименті;
– середнє арифметичне значення параметру оптимізації в j – експерименті; 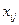 – кодове значення (±1) фактора і або ефекту взаємодії факторів у j-му експерименті.
– кодове значення (±1) фактора і або ефекту взаємодії факторів у j-му експерименті.
 Sbi2 –дисперсія і-го коефіцієнта, яка знаходиться за формулою
Sbi2 –дисперсія і-го коефіцієнта, яка знаходиться за формулою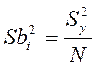
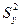 – дисперсія параметра оптимізації.
– дисперсія параметра оптимізації.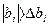 Статистично не значимі коефіцієнти можуть бути виключені з рівняння моделі.
Статистично не значимі коефіцієнти можуть бути виключені з рівняння моделі.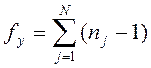 , де N– кількість експериментів у матриці планування; j – номер експерименту або точка матриці планування; n – кількість паралельних експериментів в ј-ій точці матриці планування.
, де N– кількість експериментів у матриці планування; j – номер експерименту або точка матриці планування; n – кількість паралельних експериментів в ј-ій точці матриці планування.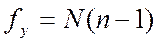 , n – однакова для всіх рядків матриці планування кількість паралельних експериментів.
, n – однакова для всіх рядків матриці планування кількість паралельних експериментів.