Однорідність дисперсії означає, що серед усіх дисперсій нема таких, які б значно перевищували одна одну. Перевірка однорідності проводиться за допомогою різних статистичних критеріїв.
Найпростішим з них є критерій Фішера (F- критерій), який служить для порівняння двох дисперсій та представляє собою відношення більшої дисперсії до меншої Fp= S12/ S22>1
Якщо Fp<Fтабл для відповідної кількості ступенів свободи та прийнятого рівня значимості, то дисперсії однорідні і навпаки. Для знаходження Fт необхідні два вхідні параметри f1i f2: кількості ступенів свободи відповідно для більшої і меншої дисперсій.
Для порівняння великої кількості дисперсій їх однорідність перевіряється за допомогою критерію Кохрена або Бартлета.
Якщо для всіх рядків матриці виконана однакова кількість паралельних експериментів і при цьому одна з дисперсій значно перевищує іншу, то однорідність ряду дисперсій перевіряється за допомогою критерію Кохрена.
Критерій Кохрена представляє собою відношення максимальної дисперсії до суми всіх дисперсій 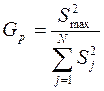 якщо Gp<Gт – дисперсії однорідні; навпаки – неоднорідні.
якщо Gp<Gт – дисперсії однорідні; навпаки – неоднорідні.
Вхідними параметрами для знаходження Gт є: N – кількість порівнюваних дисперсій, f – кількість ступенів свободи (f = n-1).
При неоднаковій кількості паралельних експериментів однорідного ряду дисперсій ряду дисперсій перевіряють за критерієм Бартлета.
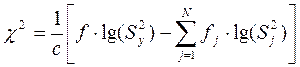 ;
; 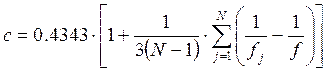 .
.
Розрахункове значення перевіряють за табличним значенням. Вхідними параметрами для знаходження 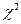 є f = n-1.
є f = n-1.


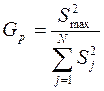 якщо Gp<Gт – дисперсії однорідні; навпаки – неоднорідні.
якщо Gp<Gт – дисперсії однорідні; навпаки – неоднорідні.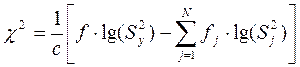 ;
; 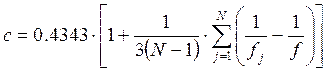 .
.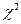 є f = n-1.
є f = n-1.