За формулою 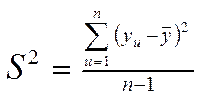 (1) можна розрахувати дисперсію в кожному експерименті ( в кожному рядку матриці планування).
(1) можна розрахувати дисперсію в кожному експерименті ( в кожному рядку матриці планування).
Дисперсія всього експерименту, або дисперсія параметру оптимізації розраховують за формулою 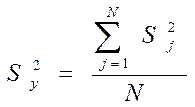 (5) Sy2 - дисперсія всього експерименту; Sj2- дисперсія j-го експерименту матриці, яка визначається за формулою (1); N- кількість експериментів в матриці. Формулою (5) користуються якщо кількість паралельних експериментів в матриці однакова. На практиці часто зустрічаються випадки, коли кількість паралельних експериментів не однакова ( відкидання помилкового експерименту, невпевненість експериментатора і дублювання експерименту).
(5) Sy2 - дисперсія всього експерименту; Sj2- дисперсія j-го експерименту матриці, яка визначається за формулою (1); N- кількість експериментів в матриці. Формулою (5) користуються якщо кількість паралельних експериментів в матриці однакова. На практиці часто зустрічаються випадки, коли кількість паралельних експериментів не однакова ( відкидання помилкового експерименту, невпевненість експериментатора і дублювання експерименту).
В цьому випадку дисперсію експерименту розраховують так: 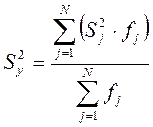 (6) де
(6) де  - кількість ступенів свободи в j-му експерименті
- кількість ступенів свободи в j-му експерименті  = nj-1 ;
= nj-1 ;
nj –кількість експериментів в j-му рядку матриці.
Зустрічаються випадки, коли експерименти матриці планування не дублюються, коли розсіяння значень параметра оптимізації не перевищує розсіяння у нульовій точці. В таких випадках для обчислення дисперсії параметра оптимізації виконуються паралельні експерименти тільки в нульо-вій точці і дисперсія при цьому дорівнює 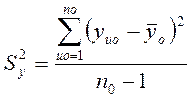 n0- кількість паралельних експериментів у нульовій точці.
n0- кількість паралельних експериментів у нульовій точці.
Формули (5) і (6) справедливі, якщо дисперсії в кожному експерименті матриці однорідні, тому перевіряють дисперсії на однорідність, тому проводять перевірку дисперсії на однорідність.


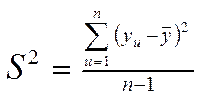 (1) можна розрахувати дисперсію в кожному експерименті ( в кожному рядку матриці планування).
(1) можна розрахувати дисперсію в кожному експерименті ( в кожному рядку матриці планування).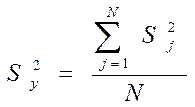 (5) Sy2 - дисперсія всього експерименту; Sj2- дисперсія j-го експерименту матриці, яка визначається за формулою (1); N- кількість експериментів в матриці. Формулою (5) користуються якщо кількість паралельних експериментів в матриці однакова. На практиці часто зустрічаються випадки, коли кількість паралельних експериментів не однакова ( відкидання помилкового експерименту, невпевненість експериментатора і дублювання експерименту).
(5) Sy2 - дисперсія всього експерименту; Sj2- дисперсія j-го експерименту матриці, яка визначається за формулою (1); N- кількість експериментів в матриці. Формулою (5) користуються якщо кількість паралельних експериментів в матриці однакова. На практиці часто зустрічаються випадки, коли кількість паралельних експериментів не однакова ( відкидання помилкового експерименту, невпевненість експериментатора і дублювання експерименту).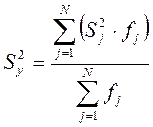 (6) де
(6) де  - кількість ступенів свободи в j-му експерименті
- кількість ступенів свободи в j-му експерименті 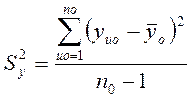 n0- кількість паралельних експериментів у нульовій точці.
n0- кількість паралельних експериментів у нульовій точці.