Необхідне для переводу натуральних величин факторів в безрозмірні величини, щоб мати можливість побудови матриці планування експерименту.
Кодування факторів здійсн. за наступною формулою
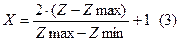 , де Х – кодоване значення фактора, Z – значення фактора взяте всередині інтервалу варіювання в натуральних одиницях виміру, Zmax та Zmin – верхній та нижній рівні факторів натуральних одиницях. З (3) виходить, що кодовані Хверхн=+1, Хнижн=-1, Хосн=0. Для простоти запису одиниці не пишуть, а пишуть “+” або “-“.
, де Х – кодоване значення фактора, Z – значення фактора взяте всередині інтервалу варіювання в натуральних одиницях виміру, Zmax та Zmin – верхній та нижній рівні факторів натуральних одиницях. З (3) виходить, що кодовані Хверхн=+1, Хнижн=-1, Хосн=0. Для простоти запису одиниці не пишуть, а пишуть “+” або “-“.
При кодуванні факторів заповнюють таблицю.
| Назва
| Натуральне значення фактору
| Кодоване значення факору
|
| V, м/хв
| S, мм/об
| ........
| t, мм
| X1
| X2
| ….
| Xk
|
| нульовий рівень
|
|
|
|
|
|
|
|
|
| інтервал варіювання
|
| 0.5
|
|
| -1
| -1
| -1
| -1
|
| верхн.
|
| 1.5
|
|
| +1
| +1
| +1
| +1
|
| ниж.
|
| 0.5
|
|
| -1
| -1
| -1
| -1
|
13. Складання матриці планування ПФЕ типу 22
Матриця планування називається таблиця умов проведення експерименту в якій рядки відповідають різним експериментам, а стовпці – різним значенням факторів. Складання матриці експерименту проводиться за правилом чергування знаків: для 1-го фактора рівні чергуються в кожному експерименті, для 2-го – через два експерименти, для 3-го – через чотири, 4-го – через вісім і т.д.
Кількість можливих експериментів ПФЕ визначається N=Pk, де N – кількість експериментів, p – кількість рівнів, k – кількість факторів.
Експерименти заносяться у стовпчик параметр експерименту “Y”
Приклад складання матриці планування ПФЕ типу 22.
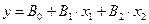
| №
| х1
| х2
| Y
|
|
| +
| +
| Y1
|
|
| -
| +
| Y2
|
|
| +
| -
| Y3
|
|
| -
| -
| Y4
|
Складання розширеної матриці. У випадку, якщо лінійна модель буде не адекватною, то прагнуть отримати не лінійну модель: 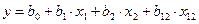 . Матриця планування з урахуванням взаємодій складається таким чином:
. Матриця планування з урахуванням взаємодій складається таким чином:
1. Спочатку будується матриця без взаємодій факторів.
2. До цієї матриці добудовують стовпці взаємодій факторів за правилом перемноження стовпців факторів, які входять в ефект взаємодії.
| №
| х1
| х2
| х1*х2
| Y
|
|
| +
| +
| +
| Y1
|
|
| -
| +
| -
| Y2
|
|
| +
| -
| -
| Y3
|
|
| -
| -
| +
| Y4
|
Ефект взаємодії 2-ох факторів – ефект 1-го порядку. Ефект взаємодії максим. порядку має порядок на одиницю менший кількості факторів. Кількість можливих взаємодій деякого характеру розраховують за формулою: 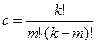 , де k – кількість факторів, m – кількість елементів у взаємодії.
, де k – кількість факторів, m – кількість елементів у взаємодії.
Властивості матриць ПФЕ.
1) Симетричність - алгебраїчна сума елементів стовпця кожного фактора дор. 0.
2) Нормування – сума квадратів елементів кожного стовпця дор. кількості експериментів.
3) Ортогональність – сума порядкових множень будь-яких двох стовпців матриці дор. 0.
4) Рототабельність – точки у матриці планування підбираються таким чином, щоб точність передбачення значень параметрів оптимізації була однакова на відстанях від центру і не залежала від напряму.


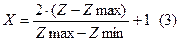 , де Х – кодоване значення фактора, Z – значення фактора взяте всередині інтервалу варіювання в натуральних одиницях виміру, Zmax та Zmin – верхній та нижній рівні факторів натуральних одиницях. З (3) виходить, що кодовані Хверхн=+1, Хнижн=-1, Хосн=0. Для простоти запису одиниці не пишуть, а пишуть “+” або “-“.
, де Х – кодоване значення фактора, Z – значення фактора взяте всередині інтервалу варіювання в натуральних одиницях виміру, Zmax та Zmin – верхній та нижній рівні факторів натуральних одиницях. З (3) виходить, що кодовані Хверхн=+1, Хнижн=-1, Хосн=0. Для простоти запису одиниці не пишуть, а пишуть “+” або “-“.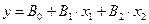
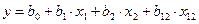 . Матриця планування з урахуванням взаємодій складається таким чином:
. Матриця планування з урахуванням взаємодій складається таким чином: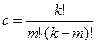 , де k – кількість факторів, m – кількість елементів у взаємодії.
, де k – кількість факторів, m – кількість елементів у взаємодії.