У загальному випадку функції схеми подаються дробово-раціональними функціями виду [4]:
 ,
,
де A(p) та B(p) – багаточлени деякого ступеню комплексної змінної p з речовинними коефіцієнтами:
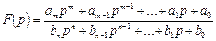
Вторинні параметри, стосовні до входу, називають вхідними функціями  . Прохідні, передатні функції:
. Прохідні, передатні функції:  . До вихідних функцій відносяться
. До вихідних функцій відносяться  .
.
Функції схеми подаються різноманітними методами в залежності від мети дослідження та прийнятого виду аналізу. Визначення функції схеми зводиться до одержання числових значень поліноміальних коефіцієнтів, або подання їх у символічній (алгебраїчній) формі через параметри компонентів схеми. Якщо відомі корені zi числівника і корені pi знаменника, функція може бути записана у виді:
 ,
,
де  .
.
Величину  називають нулями функції, оскільки при p=zi числівник А(р) буде в збігатись в нуль. При p=pi функція може приймати нескінченно велике значення, тому pi називають полюсами функції. Оскільки коефіцієнти a та b – речовинні числа, то комплексні або фіктивні нулі можуть бути тільки попарно сполучені.
називають нулями функції, оскільки при p=zi числівник А(р) буде в збігатись в нуль. При p=pi функція може приймати нескінченно велике значення, тому pi називають полюсами функції. Оскільки коефіцієнти a та b – речовинні числа, то комплексні або фіктивні нулі можуть бути тільки попарно сполучені.
Подаючи оператор у виді p=σ+jω, можна записати:
 ,
,
або
 .
.
Розташування нулів та полюсів функції у комплексній площині залежить від співвідношень між параметрами схеми [4]. Полюси функції завжди речовинні (розташовуються на речовинній осі у лівій напівплощині). Нулі можуть розташуватися у залежності від знаку речовинної їхньої частини у будь-який з напівплощин.
При синтезі активних та пасивних аналогових фільтрів в програмах ECAD ця інформація подається у вигляді координат нулів і полюсів на комплексній площині та є одним зі способів визначення параметрів передаточної характеристики фільтра. Також такі графіки можна отримати в постпроцесорі, при умові завдання відповідних виразів по осям при аналізі частотних характеристик.
6.2.1 Дослідження функцій схем у частотному діапазоні
При гармонійному сигналі на вході змінна p приймає вид  та функція схеми задається у виді:
та функція схеми задається у виді: 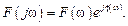
Залежність модуля  від частоти називається АЧХ, а фази передаточної функції
від частоти називається АЧХ, а фази передаточної функції  від частоти – ФЧХ:
від частоти – ФЧХ:
 ,
,  .
.
Частотні характеристики можна отримати по графічному зображенню  та
та  у комплексній площині або аналітичні по функції
у комплексній площині або аналітичні по функції  при
при  . Частотні характеристики, що отримуються при гармонійному сигналі на вході, характеризують реакцію схеми при будь-якому збудженні, оскільки періодичні сигнали можна розкласти на гармоніки рядом Фур’є.
. Частотні характеристики, що отримуються при гармонійному сигналі на вході, характеризують реакцію схеми при будь-якому збудженні, оскільки періодичні сигнали можна розкласти на гармоніки рядом Фур’є.
Схема не викривлює (не спотворює) сигнал при передачі, якщо збудження та реакція на її вході та виході зв'язані:  , де
, де  – імпульсна характеристика схеми. Отже, форма вхідного сигналу зберігається при передачі, якщо усі його елементи запізнюються на одну й ту ж величину
– імпульсна характеристика схеми. Отже, форма вхідного сигналу зберігається при передачі, якщо усі його елементи запізнюються на одну й ту ж величину  (за наявності реактивних елементів). Частотні характеристики ідеальної схеми мають вид (рисунок 6.1, а). У реальних схемах відсутність викривлення можливе лише у деякому діапазоні частот, який називають смугою пропускання:
(за наявності реактивних елементів). Частотні характеристики ідеальної схеми мають вид (рисунок 6.1, а). У реальних схемах відсутність викривлення можливе лише у деякому діапазоні частот, який називають смугою пропускання:  .
.
Оскільки складові сигналу можуть мати будь-яку частоту у діапазоні  , умови невикривленої передачі такі:
, умови невикривленої передачі такі:
- АЧХ не повинна залежати від частоти.
- фаза повинна бути пропорційна частоті сигналів збудження.
Граничні верхня та нижня частоти визначаються при рівності модуля функції  , де
, де  – значення модуля у смузі пропускання. Потужність, що віддається навантаженню при
– значення модуля у смузі пропускання. Потужність, що віддається навантаженню при  у два рази менша за потужність при
у два рази менша за потужність при  . Також можна визначити границі смуги при спаданні коефіцієнта передачі на три децибели. Децибел визначається логарифмом співвідношення потужностей:
. Також можна визначити границі смуги при спаданні коефіцієнта передачі на три децибели. Децибел визначається логарифмом співвідношення потужностей:
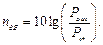
Як правило, для електронних приладів зв'язок між частотною та фазовою характеристикою однозначний. Одна з теорем, що пов'язує частотні характеристики схемної функції формулюється так: площа під фазовою кривою пропорційна різності коефіцієнтів підсилення на нескінченно високих і нульових частотах. Аналітичне співвідношення між модулем і фазою є лише для схемних функцій першого порядку. У загальному випадку фазове зрушення визначають за нахилом АЧХ по крапках.
Інколи АЧХ і ФЧХ будують у логарифмічному масштабі по осі частот, модуль будується теж у логарифмічному масштабі:
 .
.
Частотні характеристики реальної схеми наведені на рисунку 6.1,б.


 Амплітудно-фазова характеристика (АФХ) будується у полярних координатах та об'єднує АЧХ та ФЧХ (частотний годограф) [4]. АЧХ визначається довжиною вектору, а ФЧХ кутом з фіктивною віссю. При
Амплітудно-фазова характеристика (АФХ) будується у полярних координатах та об'єднує АЧХ та ФЧХ (частотний годограф) [4]. АЧХ визначається довжиною вектору, а ФЧХ кутом з фіктивною віссю. При  говорять про відставання по фазі, при
говорять про відставання по фазі, при  – про випередження.
– про випередження.
Розглянемо методи дослідження функцій часу, які використовуються для одержання точних рішень при ручному або частково автоматизованому розрахунку [4-6].
6.2.2 Дослідження функцій схеми у часовій області
Реакція схеми на одиничний імпульс називається імпульсною характеристикою та знаходиться при зворотному перетворенні функції схеми:
 .
.
Реакція схеми на одиничну функцію (стрибок напруги) називається перехідною характеристикою
 .
.
Імпульсна та перехідна характеристики зв'язані:
 .
.
Вид імпульсної та перехідної характеристик залежить від співвідношення параметрів схеми, та у кінцевому підсумку, від коефіцієнту відносного згасання ξ.
6.2.3 Зв`язок між частотними і часовими характеристиками
Частотні та часові характеристики описують ту ж саму схемну функцію та можуть бути визначені по її карті нулів та полюсів, тому між ними є зв'язок. Інколи важливо знати не точний хід перехідних та частотних характеристик, а співвідношення між їхніми параметрами, що описуються: часом наростання tH та викидом перехідної характеристики γ, з одного боку, і смуги пропускання і резонансним підйомом частотної характеристики kM, з іншого. Інакше кажучи, в ключовому пристрої при мінімальних фронтах перемикання ці процеси на АЧХ представлені зрушенням граничної частоти в область ВЧ. Для схемних функцій вищих порядків визначити співвідношення аналітично не завжди вдається, тому використовують емпіричні формули:
 ;
; 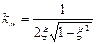 ;
;  ,
,
де ξ – коефіцієнт відносного згасання схеми, чим він менший, тим більші викиди γ та kM, причому викид виникає при ξ<1, а резонансний підйом kM – при ξ<0.707. При збільшенні смуги пропускання зменшується час наростання перехідної характеристики.
6.3 Стійкість схем
Як відомо, функція схеми має вид
 ,
,
причому, при рівності нулю одного з коренів характеристичної функції B(p), функція F(p) прагне до нескінченності, що може викликати автозбудження схеми. Тому для дослідження тривкості (стійкості) схем знаходять корені знаменника F(p), що у загальному виді називається характеристичним рівнянням. Схема буде стійкіше, якщо усі речовинні коріння та усі речовинні частини комплексних коренів характеристичного рівняння схеми у замкнутому стані будуть негативні (тобто немає коріння у правій напівплощині).
 Для нелінійних схем, що досліджуються за допомогою лінеаризованих рівнянь, умова тривкості справедлива лише для малих збурень. Отже, задача дослідження стійкості схеми зводиться до визначення знаків речовинних частин коренів характеристичного рівняння схеми зі зворотним зв'язком або встановленню розташування цих коренів на комплексній площині. На практиці застосовуються побічні методи аналізу схем на тривкість, що називаються критеріями тривкості [10].
Для нелінійних схем, що досліджуються за допомогою лінеаризованих рівнянь, умова тривкості справедлива лише для малих збурень. Отже, задача дослідження стійкості схеми зводиться до визначення знаків речовинних частин коренів характеристичного рівняння схеми зі зворотним зв'язком або встановленню розташування цих коренів на комплексній площині. На практиці застосовуються побічні методи аналізу схем на тривкість, що називаються критеріями тривкості [10].
| Рисунок 6.2 - Вплив НЗЗ на АЧХ
| |
При введенні негативного зворотного зв'язку (НЗЗ) у схему, полюси передатної функції зміщуються ліворуч від фіктивної осі. При цьому збільшується смуга пропускання, оскільки коефіцієнт широкосмугості kΔω=const. Однак, внаслідок появи резонансних викидів (при ξ<0.707) коефіцієнт широкосмугості (рис. 6.2) може збільшуватися.
Навіть у приладах твердотільної електроніки існують зворотні зв’язки, в загальному випадку – це негативний зв’язок (ефект Міллєра), який може бути як статичним, так і динамічним. У біполярному транзисторі елементом зворотного зв'язку є провідність колектора, в ПТКП – опір витоку, у МОНТ– прохідна ємність [6, 12]. У загальному випадку, електронна схема є системою із багатоканальним зворотним зв'язком.
Існують: алгебраїчний критерій Рауса – Гурвиця, частотні критерії Михайлова та Найквіста, логарифмічний частотний критерій Боде; іммітансний критерій, який зручний для аналізу схем на ВЧ зі складними внутрішніми ЗЗ [4]. Кореневим годографом називають траєкторії, що описується коренем характеристичного рівняння у комплексній площині при зміні загального коефіцієнту підсилення від  до
до  . Вивчаючи вигляд кореневого годографа, можна визначити і вид автоколивання у схемі. Користуючись методом кореневого годографа, можна не тільки робити висновки про тривалість схеми, але й визначати необхідні значення її елементів, при яких реалізуються задані частотно-часові характеристики.
. Вивчаючи вигляд кореневого годографа, можна визначити і вид автоколивання у схемі. Користуючись методом кореневого годографа, можна не тільки робити висновки про тривалість схеми, але й визначати необхідні значення її елементів, при яких реалізуються задані частотно-часові характеристики.
6.4 Дослідження функцій схем у програмах аналізу
При автоматизованому дослідженні функцій схеми у частотному діапазоні (режим АС analysis) спочатку розраховується схема по постійному струму, після цього лінеаризуються усі лінійні компоненти, та виконується розрахунок комплексної амплітуди вузлових потенціалів. До входу схеми має бути підключене джерело синусоїдального або імпульсного сигналів, комплексна амплітуда якого вважається рівною 1В, а початкова фаза рівній нулю (незалежно від того, як задані значення параметрів моделей джерел сигналів). Частота змінюється у директивах завдання на аналіз. Якщо є одне джерело вхідного сигналу, те вихідні напруги будуть співпадати з частотними характеристиками лінеаризованої моделі пристрою (електронної схеми), якщо джерел (незалежних) декілька, то відгуки від кожного сигналу будуть складатися (згідно принципу суперпозиції). ММС в частотному аналізі отримуються як СЛАР із комплексними коефіцієнтами та розв’язується прямим методом LU – розкладу (Краута), отримані таблиці значень змінних (координатного базису) потім оброблюються в пост процесорі шляхом побудови графіків обраних функцій (треба пам’ятати, що можливості постпроцесора в цьому виді аналізу найбільш обмежені внаслідок найбільш простої форми ММС (прийняті припущені про квазілінійність і квазістаціонарність системи).
Імпульсна характеристика може бути розрахована у режимі АС шляхом використання зворотного перетворення Фур’є комплексних коефіцієнтів передачі, наприклад в Digital Signal Processing (DSP) – підпрограмі цифрової обробки сигналів, в якій задаються межі інтервалу частот та кількість відліків.
Передаточні функції схеми розраховуються у режимах аналізу по постійному струму при підключенні до входу ітерованого незалежного джерела напруги або струму. ММС отримується у виді СНАР, що розв’язуються (лінеаризується) методом Ньютона–Рафсона.
Всі вище перелічені можливості доступні при аналізі в режимі «Перехідні процеси», оскільки ММС для цього виду аналізу найбільш повнофункціональна (це система нелінійних неоднорідних диференціальних рівнянь).
6.5 Контрольні запитання
1 Дослідження функцій схем у програмах аналізу.
2 Поняття функцій схеми.
3 Дослідження схем в частотному діапазоні.
4 Дослідження схем в часовому діапазоні.
5 Стійкість схем.
6 Матрично-векторні параметри схеми.
7 Функції схеми та способи їхнього подання.
8 Характеристичне рівняння: карти нулів та полюсів.
9 Вплив зворотних зв'язків на функції схеми.
6.6 Індивідуальні завдання
1 Задача – отримати АЧХ і ФЧХ селективного фільтру в програмі МС, визначити вторинні параметри.
2 Задача – отримати карту нулів і полюсів селективного фільтру в програмі МС, визначити вторинні параметри.
3 Задача – отримати графіки перехідних процесів селективного фільтру в програмі МС, визначити вторинні параметри.
4 Задача – отримати графіки АФХ селективного фільтру в програмі МС, визначити вторинні параметри.
5 Методика дослідження стійкості схем.
7 ПРАКТИЧНЕ ЗАНЯТТЯ №7
«ЧИСЛОВІ МЕТОДИ ДЛЯ АНАЛІЗУ ПРОЦЕСІВ
В ЕЛЕКТРОННИХ СХЕМАХ»
7.1 Дискретні моделі
При симуляції в ECAD для спрощення процедури алгебраїзації / дискретизації, використовують дискретні моделі елементів (компонентів електронних схем). Параметри джерел в дискретних моделях визначаються попереднім станом схеми (значеннями змінних), тобто вони відбивають «пам'ять» системи, зокрема, початкові умови.
В будь-якій схемі всі реактивні елементи можна замінити їхніми дискретними моделями, ідеальну індуктивність та ємність із початковими умовами представити операторними схемами. Початкові умови можна врахувати безпосередньо в операторній схемі, додаючи в неї відповідні джерела напруги та струму, що відбивають стан змінних комутації iL та uC (initial conditions of state variables).
В лінійних схемах при постійному кроці h=const опір ємності та провідність індуктивності (параметри RC та GL) постійні, отже для всіх моментів часу матриця провідності постійна, тому трудомістка процедура формування та упорядкування цієї матриці виконується тільки раз. Від кроку до кроку змінюються тільки значення правої частини рівнянь ММС, що задають попередній стан системи (пам'ять системи, зокрема, початкові умови).
Розглянутий підхід до розрахунку перехідних процесів називається методом дискретних моделей. В результаті застосування цього методу схема заміщення математичної моделі схеми представляється композицією тільки джерел струму/напруги та провідностей/опорів. Джерелами U та J можна емулювати як генератори вхідних сигналів, так і джерела, що замінили ємності та індуктивності. Перехідний процес можна обчислювати за допомогою цих дискретних моделей, змінюючи значення джерел на кожному кроці ітераційного процесу.
В програмах автоматизованого проектування для аналізу схем використовується представлення моделей елементів в дискретному вигляді, форма якого визначається використаним методом чисельного розв`язання рівнянь ММС. Розглянемо форми дискретних моделей для автоматизованого розрахунку [11].
Закон Ома для ємності як функція часу при дискретному способі його просуванні
 (7.1)
(7.1)
є точним співвідношенням, в той же час, числові формули відтворюють наближений розв`язок.
 Наприклад, для неявної формули Ейлера
Наприклад, для неявної формули Ейлера

 . (7.2)
. (7.2)
Якщо ми апроксимуємо точний розв`язок U/ (tn+1) чисельним U/n+1, то рівняння (7.1) прийме вигляд:
 .
.  (7.3)
(7.3)
Підставивши рівняння (7.3) у (7.2) і, розв`язавши відносно in+1, отримаємо:

 Рисунок 7.1 – Дискретна модель лінійної ємності для неявного методу Ейлера Рисунок 7.1 – Дискретна модель лінійної ємності для неявного методу Ейлера
|

 (7.4)
(7.4)
Цьому співвідношенню відповідає еквівалентна схема (рисунок 7.1), яка складається з провідності 
 і джерела струму
і джерела струму 
 .
.
Аналогічно можемо отримати дискретну модель для будь-якої багатокрокової формули чисельного інтегрування.
Проведемо аналогічні міркування для лінійної індуктивності:
 (7.5)
(7.5)
Підставимо (7.5) в неявну формулу Ейлера:
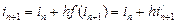
отримаємо:
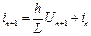
 Рисунок 7.2 – Дискретна модель
індуктивності
Рисунок 7.2 – Дискретна модель
індуктивності
|
Цьому співвідношенню відповідає дискретна модель індуктивності для неявного метода Ейлера, наведена на рисунку 7.2.
Таким чином, розрахунок перехідного процесу зводиться до розрахунку множини резистивних дискретних моделей будь-яким відомим методом.
Так, для методу вузлових потенціалів ММС прийме вигляд:
[G (y)] [j(tk+1)]=[J (y) (tk+1)],
де tk+1= (k+1) h
Вектор вузлових струмів має дві складові – незалежні джерела для моменту часу tk+1 та джерела дискретних моделей для моменту tk.
Означені підходи використовуються в ECAD.


 ,
,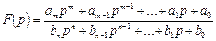
 . Прохідні, передатні функції:
. Прохідні, передатні функції:  . До вихідних функцій відносяться
. До вихідних функцій відносяться  .
. ,
, .
. називають нулями функції, оскільки при p=zi числівник А(р) буде в збігатись в нуль. При p=pi функція може приймати нескінченно велике значення, тому pi називають полюсами функції. Оскільки коефіцієнти a та b – речовинні числа, то комплексні або фіктивні нулі можуть бути тільки попарно сполучені.
називають нулями функції, оскільки при p=zi числівник А(р) буде в збігатись в нуль. При p=pi функція може приймати нескінченно велике значення, тому pi називають полюсами функції. Оскільки коефіцієнти a та b – речовинні числа, то комплексні або фіктивні нулі можуть бути тільки попарно сполучені. ,
, .
. та функція схеми задається у виді:
та функція схеми задається у виді: 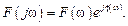
 від частоти називається АЧХ, а фази передаточної функції
від частоти називається АЧХ, а фази передаточної функції  від частоти – ФЧХ:
від частоти – ФЧХ: ,
,  .
. та
та  у комплексній площині або аналітичні по функції
у комплексній площині або аналітичні по функції  при
при  . Частотні характеристики, що отримуються при гармонійному сигналі на вході, характеризують реакцію схеми при будь-якому збудженні, оскільки періодичні сигнали можна розкласти на гармоніки рядом Фур’є.
. Частотні характеристики, що отримуються при гармонійному сигналі на вході, характеризують реакцію схеми при будь-якому збудженні, оскільки періодичні сигнали можна розкласти на гармоніки рядом Фур’є. , де
, де  – імпульсна характеристика схеми. Отже, форма вхідного сигналу зберігається при передачі, якщо усі його елементи запізнюються на одну й ту ж величину
– імпульсна характеристика схеми. Отже, форма вхідного сигналу зберігається при передачі, якщо усі його елементи запізнюються на одну й ту ж величину  (за наявності реактивних елементів). Частотні характеристики ідеальної схеми мають вид (рисунок 6.1, а). У реальних схемах відсутність викривлення можливе лише у деякому діапазоні частот, який називають смугою пропускання:
(за наявності реактивних елементів). Частотні характеристики ідеальної схеми мають вид (рисунок 6.1, а). У реальних схемах відсутність викривлення можливе лише у деякому діапазоні частот, який називають смугою пропускання:  .
. , умови невикривленої передачі такі:
, умови невикривленої передачі такі: , де
, де  – значення модуля у смузі пропускання. Потужність, що віддається навантаженню при
– значення модуля у смузі пропускання. Потужність, що віддається навантаженню при  у два рази менша за потужність при
у два рази менша за потужність при  . Також можна визначити границі смуги при спаданні коефіцієнта передачі на три децибели. Децибел визначається логарифмом співвідношення потужностей:
. Також можна визначити границі смуги при спаданні коефіцієнта передачі на три децибели. Децибел визначається логарифмом співвідношення потужностей: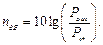
 .
.

 Амплітудно-фазова характеристика (АФХ) будується у полярних координатах та об'єднує АЧХ та ФЧХ (частотний годограф) [4]. АЧХ визначається довжиною вектору, а ФЧХ кутом з фіктивною віссю. При
Амплітудно-фазова характеристика (АФХ) будується у полярних координатах та об'єднує АЧХ та ФЧХ (частотний годограф) [4]. АЧХ визначається довжиною вектору, а ФЧХ кутом з фіктивною віссю. При  говорять про відставання по фазі, при
говорять про відставання по фазі, при  – про випередження.
– про випередження. .
. .
. .
. ;
; 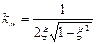 ;
;  ,
, ,
, Для нелінійних схем, що досліджуються за допомогою лінеаризованих рівнянь, умова тривкості справедлива лише для малих збурень. Отже, задача дослідження стійкості схеми зводиться до визначення знаків речовинних частин коренів характеристичного рівняння схеми зі зворотним зв'язком або встановленню розташування цих коренів на комплексній площині. На практиці застосовуються побічні методи аналізу схем на тривкість, що називаються критеріями тривкості [10].
Для нелінійних схем, що досліджуються за допомогою лінеаризованих рівнянь, умова тривкості справедлива лише для малих збурень. Отже, задача дослідження стійкості схеми зводиться до визначення знаків речовинних частин коренів характеристичного рівняння схеми зі зворотним зв'язком або встановленню розташування цих коренів на комплексній площині. На практиці застосовуються побічні методи аналізу схем на тривкість, що називаються критеріями тривкості [10]. до
до  . Вивчаючи вигляд кореневого годографа, можна визначити і вид автоколивання у схемі. Користуючись методом кореневого годографа, можна не тільки робити висновки про тривалість схеми, але й визначати необхідні значення її елементів, при яких реалізуються задані частотно-часові характеристики.
. Вивчаючи вигляд кореневого годографа, можна визначити і вид автоколивання у схемі. Користуючись методом кореневого годографа, можна не тільки робити висновки про тривалість схеми, але й визначати необхідні значення її елементів, при яких реалізуються задані частотно-часові характеристики. (7.1)
(7.1) Наприклад, для неявної формули Ейлера
Наприклад, для неявної формули Ейлера
 . (7.2)
. (7.2) .
.  (7.3)
(7.3)
 Рисунок 7.1 – Дискретна модель лінійної ємності для неявного методу Ейлера
Рисунок 7.1 – Дискретна модель лінійної ємності для неявного методу Ейлера

 (7.4)
(7.4)
 і джерела струму
і джерела струму 
 .
. (7.5)
(7.5)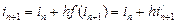
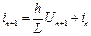
 Рисунок 7.2 – Дискретна модель
індуктивності
Рисунок 7.2 – Дискретна модель
індуктивності