 У разіроботи одного пристрою дану задачу можна подати у вигляді одноканальної СМО з необмеженою чергою.
У разіроботи одного пристрою дану задачу можна подати у вигляді одноканальної СМО з необмеженою чергою.
Рис.3. Граф СМО з очікуванням
Стан S0 відповідає вільному каналу; S1 – канал зайнятий і черги немає, S2 – канал зайнятий і одне замовлення пербуває у черзі; S3 – у черзі два замовлення і т.д. У стані Sk – канал зайнятий і у черзі к - 1 замовлення. За стрілками зліва направо систему з одного стану в інший переводить потік замовлень інтенсивністю l, а за стрілками справа наліво - потік обслуговувань інтенсивністю m. Кожного разу під час переходу з одного стану в інший черга змінюється на одиницю.
Для визначення ймовірності початкового стану можна використати рівняння (4).
lр0 = mр1.
Звідси
р1=(l/m)p0.
Величину інтенсивністі навантаження визначаємо за формулою:
r=l/m=0,33
Для стійкої роботи СМО з очікуванням потрібно, щоб середня інтенсивність потоку обслуговування була більше інтенсивності потоку замовлень, тобто l < m, отже, r < 1. Якщо l > m, система не впорається з обслуговуванням і черга буде зростати до нескінченності.
З використанням введених позначень, ймовірність стану S1 можна записати у вигляді:
р1=rp0. (9)
Використовуємо рівняння Колмогорова для стану S1:
lp1+mp1=lp0+mp2.
Оскільки lp0=mp1 та mp2=lp1,
p2=p1l¤m = r2 p0.
Аналогічно для стану S2: p3 = r3 p0 . І.т.д.:
pk=rk×p0. (10)
Для визначення р0 запишемо вираз для суми ймовірностей:
p0 + r p0 + r2 p0 +…+ rk p0 = 1.
Звідси отримуємо
pk=rk(1-r). (11)
Використовуючи цей вираз, можна визнаємо характеристики СМО з очікуванням, важливі для її функціонування: середню довжину черги Lq, середнє число замовлень в системі Ls, середній час перебування замовлення в системі Ws, середня тривалість очікування замовлення у черзі Wq і ймовірність утворення черги рк.
З ймовірністю p2 у черзі перебуває одне замовлення, з ймовірністю p3 – два замовлення і з ймовірністю pk у черзі – (k-1) замовлення.
Отже,
Lq=1p2 +2p3 +…+(k-1)pk=r2(1-r)(1+2r+3r2+…+krk-1).
Тому середня довжина черги:
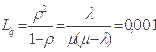
Середня кількість замовлень, що перебуває у системі обслуговування Ls, складається з середньої кількості замовлень у черзі та середньої кількості замовлень на обслуговуванні (включаючи інтервали, коли черги не було):
Ls=0p0+1p1+2p2+…+ kpk.
Ця величина набуває значення 0, коли канал вільний, ймовірність такого стану дорівнює p0 = 1 - r.
Якщо канал зайнятий і одне замовлення обслуговуються Ls = 1, ймовірність такої події: p1=1 – p0 = r.
Отже,
 (12)
(12)
Середній час очікування у черзідорівнює середній кількості замовлень у черзі, поділеному на інтенсивність потоку обслуговування:
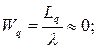
Ймовірність утворення чергидорівнює ймовірності того, що у системі буде більше однієї вимоги, тобто:
Pk = 1– p0 – p1=1– (1 – r) – r(1 – r) = r2(13)
Середній час перебування замовлення у системі
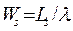 =1.
=1.


 У разіроботи одного пристрою дану задачу можна подати у вигляді одноканальної СМО з необмеженою чергою.
У разіроботи одного пристрою дану задачу можна подати у вигляді одноканальної СМО з необмеженою чергою.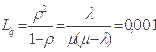
 (12)
(12)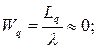
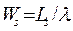 =1.
=1.