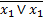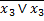Після мінімізації логічної функції є побудова її структурної схеми (синтез). Початковими даними для цієї операції є, як правило, МДНФ або МКНФ логічної функції.
Визначальну роль у забезпеченні критерію за мінімумом апаратурних затрат відіграє елементний базис, тобто певний набір функціональних ЛЕ.
L AQItABQABgAIAAAAIQDqcZPZ4AAAAAgBAAAPAAAAAAAAAAAAAAAAAHgGAABkcnMvZG93bnJldi54 bWxQSwUGAAAAAAQABADzAAAAhQcAAAAA ">
B Ai0AFAAGAAgAAAAhABuwIk7fAAAACAEAAA8AAAAAAAAAAAAAAAAAeAYAAGRycy9kb3ducmV2Lnht bFBLBQYAAAAABAAEAPMAAACEBwAAAAA= ">
2І-НЕ 3І-НЕ 4І-НЕ 2І
8І-НЕ 2АБО-НЕ 3АБО-НЕ 4АБО-НЕ
8АБО-НЕ НЕ 2-4І-АБО-НЕ
Якщо базис наперед не заданий, то при синтезі жодних перетворень з логічною функцією робити не потрібно, досить лише структурно реалізувати за допомогою ЛЕ всі її логічні операції.
Наприклад,
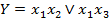
x1 x2 x3

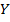
Однак, якщо базис за умовою наперед заданий, дану логічну функцію необхідно спеціально перетворити. Головна мета цих перетворень – зведення виразу функції до заданого базису. Це означає, що в кінцевому виразі логічної функції мають «проглядатися» всі операції, символи і кількість змінних, тобто всі ознаки, які властиві цьому базису. Наприклад, задано базис 2І-НЕ (елемент Шефера); для реалізації функції змінних відповідними перетвореннями і замінами МДНФ цієї функції має бути зображена у вигляді  , а у базисі 2АБО-НЕ (елемент Пірса) МКНФ цієї функції має бути зображена у вигляді
, а у базисі 2АБО-НЕ (елемент Пірса) МКНФ цієї функції має бути зображена у вигляді 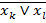 .
.
При базисі 2-2І-АБО-НЕ логічна функція має набувати остаточного вигляду 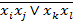
Приклад 2. Реалізувати в базисі 2І-НЕ логічну функцію.
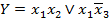
Методика:
1. Застосувати аксіому про подвійну інверсію
2. Застосувати правило де Моргана
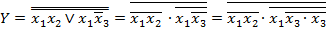
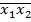
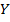
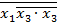
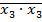
Приклад 3. Реалізувати в базисі 3АБО-НЕ логічну функцію
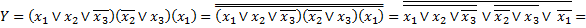
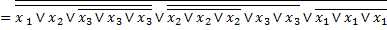
x1 x2 x3
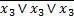
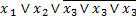
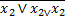
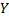
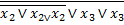
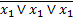
Приклад 4. У базисі суматора за модулем 2 реалізувати логічну функцію приведену у прикладі 2 (мінімізація логічних функцій)
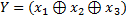 x1 x2 x3
x1 x2 x3
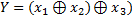
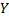
Приклад 5. В базисі 2АБО-НЕ (елемент Пірса) побудувати структурну схему для логічної функції
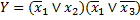
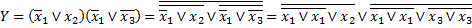 ,
,
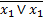
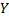
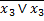


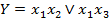
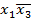

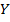
 , а у базисі 2АБО-НЕ (елемент Пірса) МКНФ цієї функції має бути зображена у вигляді
, а у базисі 2АБО-НЕ (елемент Пірса) МКНФ цієї функції має бути зображена у вигляді 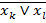 .
.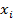
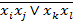

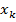

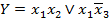
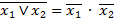
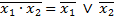
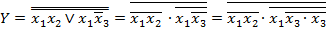
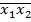
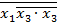
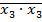
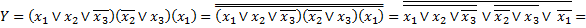
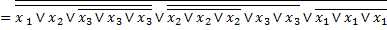
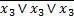
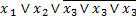
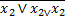
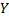
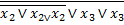
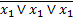
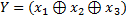 x1 x2 x3
x1 x2 x3
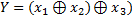
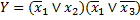
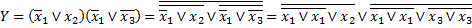 ,
,