1. Метод безпосередніх перетворень.
2. Метод карт Карно.
1. Метод безпосередніх перетворень – це аналітичний метод спрощення логічних функцій з допомогою аксіом та законів булевої алгебри. Ефективний для кількості змінних не більшій трьох.
Приклад 1.
Y= 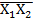 X3˅
X3˅  X2
X2 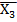 ˅
˅  X2X3˅
X2X3˅ 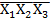 ˅X1
˅X1 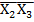 =
=  (
( 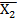 X3˅X2
X3˅X2 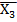 ˅X2X3˅
˅X2X3˅ 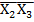 )˅X1X2
)˅X1X2 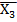 =
=
=  [
[ 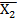 (X3˅
(X3˅ 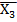 )˅X2(X2˅
)˅X2(X2˅ 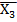 )]˅X1X2
)]˅X1X2 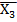 =
=  (
( 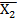 ˅X2)˅X1X2
˅X2)˅X1X2 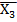 ˅
˅  X2
X2 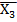 =
=  ˅X2
˅X2 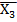 (X1˅
(X1˅  )=
)=
=X1˅X2 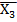 .
.
Приклад 2.
Y= 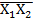 X3˅
X3˅  X2
X2 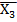 ˅X1
˅X1 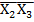 ˅X1X2X3=
˅X1X2X3=  (
( 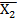 X3˅X2
X3˅X2 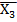 )˅X1(
)˅X1( 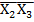 ˅X2X3)=
˅X2X3)=  (X2
(X2 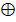 X3)˅ ˅X1(
X3)˅ ˅X1( 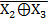 )= X1
)= X1 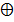 (X2
(X2 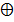 X3)=X1
X3)=X1 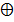 X2
X2 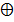 X3 – вийнятково АБО (базис).
X3 – вийнятково АБО (базис).
2. Метод карт Карно
1. Заповнюють карту Карно.
Наприклад:
Закон склеювання Х1Х2˅Х1 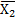 =Х1 =Х1
|
Y=X1X2  ˅X1
˅X1 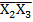 =X1
=X1  (X2˅
(X2˅ 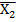 )=X1
)=X1  . – аналітично.
. – аналітично.
Тобто суть мінімізації полягає у тому, що шукають мінтерми у сусідніх клітинках, які «склеюються» за законом склеювання для диз’юнкції. У нашому випадку Х2 при покритті приймає значення для покритих клітинок і 1 і 0 і тому цей аргумент (змінна) вилучається і зчитується як Х1  . Об’єднують максимальне число клітинок, що містять «1» по 2, 4, 8 клітинки (2n). При цьому прагнуть, що кожна клітинка з «1» обов’язково входила в яке-небудь покриття.
. Об’єднують максимальне число клітинок, що містять «1» по 2, 4, 8 клітинки (2n). При цьому прагнуть, що кожна клітинка з «1» обов’язково входила в яке-небудь покриття.
Мінімізуємо за допомогою карти Карно функцію, що задана у прикладі 1.
Y= 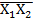 X3˅
X3˅  X2
X2 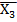 ˅
˅  X2X3˅
X2X3˅ 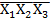 ˅X1X2
˅X1X2 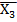 .
.
Y= 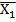 ˅Х2
˅Х2  .
.
Що значно простіше.
Отже, мінімізація прямої логічної функції за допомогою карт Карно зводиться до послідовного виконання таких операцій:
1) Розміщення конституант 1 в клітинках, які відповідають мінтермам даної функції, що зображена в УДНФ;
2) Об’єднання сусідніх «1» контурами по 2, 4 або 8 клітинок;
3) Зчитування кон’юнкцій, що входять у даний контур, вилучаючи з них за законом склеювання ті змінні, які утворюють доповнення (Хі˅ 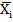 );
);
4) Об’єднання одержаних кон’юнкцій диз’юнкцією, яка є мінімізованою диз’юнктивною нормальною формою МДНФ заданої функції.
Приклад. Мінімізувати логічну функцію, задану таблицею істинності.
Зобразимо цю логічну функцію картою Карно і, дотримуючись правил мінімізації, отримаємо вираз мінімізованої диз’юнктивної форми (МДНФ):
рис.1.4___
Y=X2  ˅X3X2˅X3X1X0˅
˅X3X2˅X3X1X0˅ 
Мінімізовану кон’юнктивну форму цієї функції одержують шляхом покриття «нулів» в карті Карно (рис.1.4)
Y=(X3˅  )(
)( 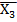 ˅X2˅X0)(X2˅X1˅
˅X2˅X0)(X2˅X1˅ 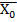 ).
).
Для синтезу цифрових пристроїв вибирають ту мінімізовану форму, яка містить менше змінних.
Мінімізація частково визначених функцій
Логічна функція називається частково визначеною, якщо для деяких двійкових наборів вона може приймати довільне значення (0 і 1).
При мінімізації частково визначених функцій набори, які є невизначені, замінюються «одиницями» або «нулями» так, щоб мінімізовані форми функцій містили якомога менше число змінних.
МДНФ: Y1=X0
| х2х1
х0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 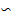 1 1
| 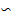 1 1
|
МДНФ: Y=X2˅X1X0.


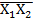 X3˅
X3˅  X2
X2 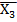 ˅
˅ 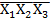 ˅X1
˅X1 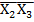 =
= 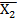 X3˅X2
X3˅X2 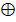 X3)˅ ˅X1(
X3)˅ ˅X1( 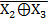 )= X1
)= X1 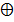 (X2
(X2 
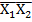
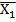 Х2
Х2
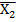
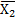 =Х1
=Х1
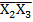 =X1
=X1 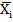 );
);
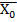 ).
).