1. Словесне зображення – це логічне висловлення, під яким розуміють довільнетвердження, щодо якого можна сказати, істинне воно, чи хибне. Наприклад, функція хибна тоді і тільки тоді х1 істинне, а х2 хибне (Y =  ˅ X2).
˅ X2).
2. Табличне зображення – функція задається таблицею істинності, в якій показано, на яких наборах вона набуває значень 1 чи 0.
3. Числовий запис – функція задається у вигляді послідовності десяткових чисел, що є еквівалентами тих вхідних наборів, на яких дана функція набуває значень 1 або 0.
Наприклад:
Y =  (0,3,4,7) – Y=1;
(0,3,4,7) – Y=1;
Y =  (1,2,5,6) – Y=0.
(1,2,5,6) – Y=0.
4. Аналітичний запис – функція задається алгебраїчним виразом, який отримують при застосуванні логічних операцій алгебри логіки до змінних.
Якщо попередні форми зображення логічних функцій лише вказують значення функції на конкретних наборах змінних, то аналітичне зображення, крім того, ще дозволяє виконувати різні аналітичні перетворення, які необхідні як для аналізу, так і для синтезу цифрового пристрою, який має реалізувати дану логічну функцію.
Наприклад,
Y = X1 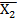 X3 ˅
X3 ˅ 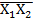 X3 ˅ X1X2.
X3 ˅ X1X2.
Найбільшраціональним є зображення логічних функцій в нормальних (канонічних) формах запису за допомогою інверсії, диз’юнкції, кон’юнкції. До них належать:
- Диз’юнктивна нормальна форма (ДНФ);
- Кон’юнктивна нормальна форма(КНФ).
У ДНФ логічна функція представляється як сума добутків окремих виразів функції змінних з інверсією і без інверсії (диз’юнкція кон’юнкцій). Наприклад,
Y = X1 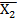 ˅
˅ 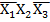 ˅ X1
˅ X1 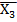 . (1)
. (1)
причому всі змінні Хі = 1, а 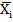 = 0.
= 0.
У КНФ логічна функція представляється як добуток суми окремих виразів функції змінних з інверсією і без інверсії (кон’юнкція диз’юнкцій). Наприклад,
Y = (X1˅ 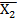 )(
)( 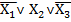 )(X1˅
)(X1˅ 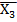 ), (2)
), (2)
причому всі змінні Хі = 0, а 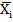 = 1.
= 1.
Крім ДНФ і КНФ використовують так звані повні або удосконалені форми зображення логічних функцій УДНФ і УКНФ.
В них кожен вираз, що входить у задану функцію, має містити всі аргументи.
Для перетворення функції (1) до УДНФ необхідно в перший вираз ввести відсутній аргумент Х3, а у третій вираз – Х2. Для цього користуються аксіомою доповнення (Хі˅ Хі =1).
Тоді отримуємо:
y= x1 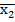 (x3
(x3 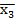 )˅
)˅ 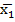 x2
x2 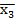 ˅(x1˅
˅(x1˅ 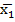 )x2
)x2 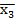 = x1
= x1 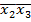 ˅x1
˅x1 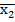 x3˅
x3˅ 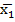 x2
x2 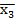 ˅x1x2
˅x1x2  = x1
= x1 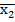 x3˅
x3˅
˅ x1 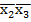 ˅
˅ 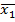 x2
x2 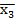 ˅x1x2
˅x1x2 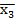
В УДНФ окремівирази (члени) називаються мінтермами, і у кожному з них добуток аргументів дорівнює 1.
Для перетворення функції, заданої в КНФ, в УКНФ відсутні змінні вводяться шляхом застосування закону склеювання (х1˅х2)(х1˅ 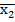 ) = х1.
) = х1.
Тому з виразу (2) переходимо до УКНФ за допомогою наступних перетворень:
у = (x1˅ 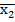 )(
)( 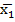 ˅x2˅
˅x2˅ 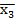 )(
)( 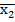 ˅x3) = (x1˅
˅x3) = (x1˅ 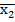 ˅x3)(x1˅
˅x3)(x1˅ 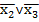 )(
)( 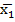 ˅x2˅
˅x2˅ 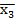 )(x1˅
)(x1˅ 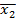 ˅
˅ 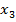 )(
)( 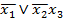 )= =(x1˅
)= =(x1˅ 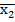 ˅x3)
˅x3) 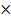 (x1˅
(x1˅ 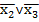 )(
)( 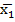 ˅x2˅
˅x2˅ 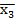 )(
)(  ).
).
В УКНФ окремі вирази (члени) називаються макстермами, і у кожному з них сума аргументів дорівнює нулю.
Такі форми зображення зручні для проектування цифрових пристроїв.
Для переходу від числового запису, чи табличного зображення логічної функції до її аналітичного зображення роблять так:
- для зображення в УДНФ виписують ті набори змінних, для яких функція дорівнює «1»; для кожного такого набору складають мінтерм, причому змінні хі = 0 замінюють на 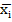 і одержані мінтерми з’єднують диз’юнкцією (логічним додаванням);
і одержані мінтерми з’єднують диз’юнкцією (логічним додаванням);
- для зображення в УКНФ виписують набори змінних, для яких дана функція дорівнює «нулю» , для кожного такого набору складають макстерм, причому змінні хі= 1 замінюють на 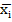 і одержані макстерми об’єднують кон’юнкцією (логічним множенням).
і одержані макстерми об’єднують кон’юнкцією (логічним множенням).
Для переходу зображення логічної функції з ДНФ в КНФ і навпаки використовують правило Шеннона: інверсна функціяотримується шляхом заміни всіх змінних на інверсні їм, знаків диз’юнкції на знаки кон’юнкції, а знаків кон’юнкції – на знаки диз’юнкції.
Приклад.
у = х1·х2 ˅ x1· 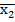 ·
· 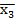 – ДНФ.
– ДНФ.
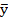 = (
= ( 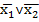 )·(
)·( 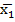 ˅x2˅x3) – КНФ.
˅x2˅x3) – КНФ.
5. Координатний спосіб зображення логічної функції найбільш поширений для числа змінних 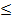 6. В його основі лежить побудова карт мінтермів або карт Карно. Карта містить m=2n клітинок, причому кожній клітинці відповідає один з m мінтермів. Тут n – число змінних (аргументів).
6. В його основі лежить побудова карт мінтермів або карт Карно. Карта містить m=2n клітинок, причому кожній клітинці відповідає один з m мінтермів. Тут n – число змінних (аргументів).
На наступному рисунку наведена карта Карно для числа змінних 4. В ній кожна клітинка має свою координату. Карта будується так, щоб сусідні клітинки відрізнялися значеннями лише однієї змінної. Сусідніми вважаються лише ті клітинки, які дотикаються своїми сторонами, а також клітинки, що розташовані на краях карти (верхній і нижній рядок, лівий і правий стовбці).
| Х3Х2
Х1Х0
|
|
|
|
|
|
|
|
| Х3 Х2 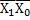
|
|
|
|
| 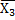 Х2 Х2 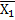 Х0 Х0
| Х3 Х2 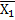 Х0 Х0
| Х3 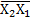 Х0 Х0
|
|
|
|
| Х3 Х2 Х1 Х0
|
|
|
|
|
|
|
|
Якщо логічна функція задана, наприклад, числовим записом у=  (0, 1, 2, 9, 11), то, враховуючи, що число аргументів є 4, карта Карно має мати 24 клітинок. У кожну клітинку з приведеним номером набору записуємо «1», а у всі інші – «0».
(0, 1, 2, 9, 11), то, враховуючи, що число аргументів є 4, карта Карно має мати 24 клітинок. У кожну клітинку з приведеним номером набору записуємо «1», а у всі інші – «0».
Приклад зображення логічної функції картою Карно.
На рис.1.2 і рис.1.3 наведені карти Карно для числа змінних (аргументів) 3 і 5 відповідно.
рис.1.2.
рис.1.3.


 ˅ X2).
˅ X2). (0,3,4,7) – Y=1;
(0,3,4,7) – Y=1; (1,2,5,6) – Y=0.
(1,2,5,6) – Y=0.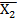 X3 ˅
X3 ˅ 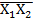 X3 ˅ X1X2.
X3 ˅ X1X2.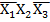 ˅ X1
˅ X1 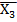 . (1)
. (1)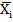 = 0.
= 0.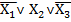 )(X1˅
)(X1˅ 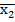 (x3
(x3 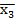 )˅
)˅ 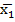 x2
x2 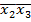 ˅x1
˅x1  = x1
= x1 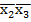 ˅
˅ 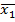 x2
x2 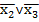 )(
)( 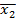 ˅
˅ 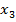 )(
)( 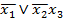 )= =(x1˅
)= =(x1˅ 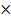 (x1˅
(x1˅  ).
).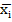 і одержані мінтерми з’єднують диз’юнкцією (логічним додаванням);
і одержані мінтерми з’єднують диз’юнкцією (логічним додаванням);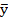 = (
= ( 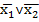 )·(
)·( 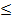 6. В його основі лежить побудова карт мінтермів або карт Карно. Карта містить m=2n клітинок, причому кожній клітинці відповідає один з m мінтермів. Тут n – число змінних (аргументів).
6. В його основі лежить побудова карт мінтермів або карт Карно. Карта містить m=2n клітинок, причому кожній клітинці відповідає один з m мінтермів. Тут n – число змінних (аргументів).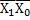
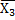 Х2
Х2 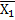 Х0
Х0
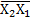 Х0
Х0
 (0, 1, 2, 9, 11), то, враховуючи, що число аргументів є 4, карта Карно має мати 24 клітинок. У кожну клітинку з приведеним номером набору записуємо «1», а у всі інші – «0».
(0, 1, 2, 9, 11), то, враховуючи, що число аргументів є 4, карта Карно має мати 24 клітинок. У кожну клітинку з приведеним номером набору записуємо «1», а у всі інші – «0».