Пристрій, що реалізує дії над двійковими числами, можна розглядати, як функціональний перетворювач (ФП) (рис.1.1) з n-входами і m-виходами, на входи якого подаються двійкові числа, а на виходах отримуємо результат перетворення також у вигляді двійкового числа.
рис.1.1
Кількість можливих наборів дорівнює 2n. Кожному набору відповідає 0 або 1 на виході.
Функцією алгебри логіки є функція, яка однозначно визначає відповідність кожного двійкового набору нулю, або одиниці. Так як число наборів аргументів є скінченним, то будь-яка функція алгебри логіки може бути задана скінченною таблицею з 2n рядками.
Можливий і аналітичний спосіб задання функції алгебри логіки – запис у вигляді логічного виразу, який показує, які логічні операції повинні виконуватися над аргументами і в якій послідовності.
Функції одного і двох аргументів називаються елементарними, якщо логічні вирази цих функцій містять не більше одної логічної операції, яка є елементарною.
1. Функція ЛОГІЧНЕ ЗАПЕРЕЧЕННЯ (НЕ) подається таблицею істинності:
і логічнимвиразомy =  .
.
На схемах пристрій, що реалізує цю логічну функцію зображається
х у і називається схема НЕ або інвертор.
2. Функція ДИЗ’ЮНКЦІЯ двох змінних (схема АБО) – логічне сумування двох змінних.
Таблиця істинності
у = х1 ˅ х2
Умовне позначення диз’юнкора на схемах
х1
y
х2
3. Функція КОН’ЮНКЦІЯ двох змінних (схема І) – логічне множення двох змінних.
Таблиця істинності
Y = X1 + X2
Умовнепозначення кон’юнктора на схемах
x1
y
x2
4. Функція Пірса – ЛОГІЧНЕ ДОДАВАННЯ двох змінних з ЗАПЕРЕЧЕННЯМ (схема АБО-НЕ)
Таблиця істинності
у = 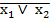
і її умовне позначення на схемах х1
x2
5. ФункціяШеффера – ЛОГІЧНЕ МНОЖЕННЯ двох змінних з ЗАПЕРЕЧЕННЯМ (схема І-НЕ)
Таблиця істинності
у = 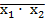
і її умовне позначення на схемах x1
x2
Функції 2-5 можуть бути функціями довільного числа аргументів
Y = X1 ˅ X2 ˅…˅ Xn Y = X1 · X2 ·…·Xn Y = 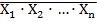
6. Функція СУМУВАННЯ за mod2, або функція нерівнозначності або нееквівалентності (схема ВИЙНЯТКОВО-АБО),
Таблиця істинності
Y = X1 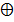 X2 = X1
X2 = X1 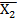 ˅
˅  X2 = (X1 ˅ X2)(
X2 = (X1 ˅ X2)(  ˅
˅ 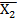 )
)
х1
іїї умовне позначення на схемах
х2
7. Функція СУМУВАННЯ за mod2 з ЗАПЕРЕЧЕННЯМ, або функція рівнозначності або еквівалентності (схема ВИЙНЯТКОВО-АБО-НЕ)
Таблиця істинності
Y = 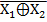 =
=  ·
· 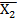 ˅ X1·X2 = (X1 ˅
˅ X1·X2 = (X1 ˅ 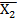 )(
)(  ˅ X2)
˅ X2)
і її умовне позначення х1
х2


 .
.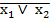
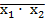
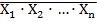
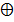 X2 = X1
X2 = X1 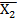 ˅
˅  X2 = (X1 ˅ X2)(
X2 = (X1 ˅ X2)( 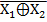 =
=