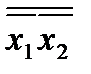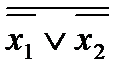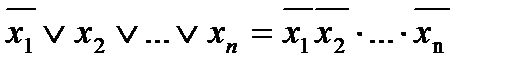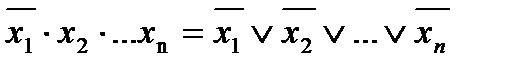1. Закон комутативності (перестановки)
х1 · х2 = х2 · х1;
х1  х2 = х2
х2 = х2  х1.
х1.
2. Закон асоціативності (сполучення)
х1 ·(х2 · х3) = (х1 ·х2) · х3;
х1  (х2
(х2  х3) = (х1
х3) = (х1  х2)
х2)  х3 = х1
х3 = х1  х2
х2  х3.
х3.
3. Закон дистрибутивності (розподілу)
х1 · (х2  х3) = х1 · х2
х3) = х1 · х2  х1 · х3;
х1 · х3;
х1  х2 · х3 = (х1
х2 · х3 = (х1  х2) · (х1
х2) · (х1  х3) .
х3) .
4. Закон склеювання
(х1  х2) · (х1
х2) · (х1 
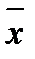 2) = х1;
2) = х1;
х1 · х2  х1 ·
х1 · 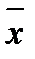 2 = х1.
2 = х1.
5. Закон поглинання
х1 ·(х1  х2) = х1;
х2) = х1;
х1  х1 · х2 = х1.
х1 · х2 = х1.
6. Закон дуальності (правило де Моргана)
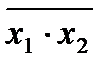 =
= 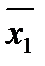

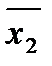 ;
;
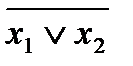 =
= 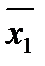 ·
· 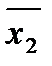
Доведення 5-го закону (поглинання для кон’юнкції):

 х1 ·(х1
х1 ·(х1  х2) = х1 · х1
х2) = х1 · х1  х1 · х2 = х1 (1
х1 · х2 = х1 (1  х2) = х1.
х2) = х1.
х1 1
Доведення закону дистрибутивності для диз’юнкції (3-й закон):
Застосовуючи закон поглинання:
х1  х2 · х3 = х1· (х1
х2 · х3 = х1· (х1  х2
х2  х3)
х3)  х2 · х3 = х1· х1
х2 · х3 = х1· х1  х1· х2
х1· х2  х1· х3
х1· х3  х2· х3 =
х2· х3 =
= х1 ·(х1  х3)
х3)  х2 ·(х1
х2 ·(х1  х3) = (х1
х3) = (х1  х2) ·(х1
х2) ·(х1  х3).
х3).
Доведення законусклеювання для кон’юнкції:

 (х1
(х1  х2) · (х1
х2) · (х1 
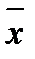 2) = х1 · х1
2) = х1 · х1  х1 ·
х1 · 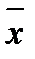 2
2  х1 · х2
х1 · х2  х2 ·
х2 · 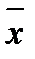 2 = х1
2 = х1  х1(х2
х1(х2 
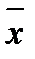 2) = х1
2) = х1  х1=х1 .
х1=х1 .
х1 0 1
Поговоримо про закони дуальності.
Правило Шеннона – для одержання алгебраїчного виразу інверсної функції
необхідно у згаданій функції всі змінні замінити на інверсні їм, всі знаки кон’юнкції – на знаки диз’юнкції, а всі знаки диз’юнкції – на знаки кон’юнкції.
Приклад: знайти інверсію логічної функції
Y = x1  x1 ·
x1 · 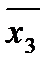
 x1
x1 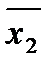 x3.
x3.
Розв’язок:

Правило де Моргана – інверсія кон’юнкції дорівнює диз’юнкції інверсій, а інверсія диз’юнкцій – кон’юнкції інверсій.
Приклад:
Y = 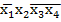 =
= 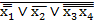 =
= 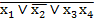 .
.
Наслідки законів дуальності
x1  x2 =
x2 = 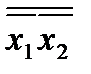
х1 · х2 = 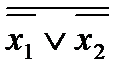
Вони справедливі для будь-якого числа змінних.
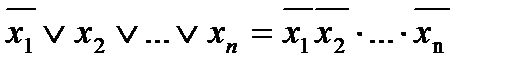
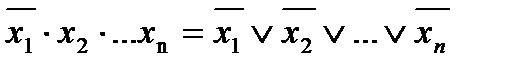


 х2 = х2
х2 = х2 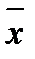 2) = х1;
2) = х1;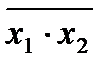 =
= 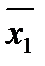
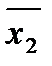 ;
;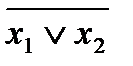 =
= 
 х1 ·(х1
х1 ·(х1 

 (х1
(х1 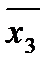
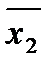 x3.
x3.
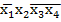 =
= 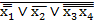 =
= 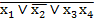 .
.