У зв’язку з двійковим зображенням цифрових сигналів, що набувають двох значень (лише 0 і 1), найзручнішим математичним апаратом для аналізу та синтезу цифрових систем є алгебра логіки (булева алгебра). У булевій алгебрі символи 0 і 1 характеризують стани змінних та їх функції і тому не можна розглядати ці символи як арифметичні числа.
Алгебра логіки – це алгебра станів, а не алгебра чисел, і їй властиві на відміну від звичайної алгебри логічні дії над станами.
1. Основне поняття алгебри логіки – висловлення – це речення, в якому міститься суть (сенс) твердження істинності або його заперечення (хибності).
Можна позначити висловлення символом, наприклад X або Y і вважати, що
Х = 1
або якщо висловлення істинне,
Y = 1
Х = 0
а якщо висловлення неістинне (хибне).
Y = 0
Оскільки будь-яка змінна (або її функція) може мати стан 0 або 1, в алгебрі логіки кожній двійковій змінній ставиться у відповідність обернена до неї (інверсна) змінна.
Так якщо Х = 0, то 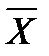 = 1,
= 1,
А якщо Х = 1, то 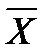 = 0.
= 0.
Подвійне заперечення 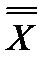 = Х.
= Х.
«  » означає логічне заперечення і називається «інверсією». Вона означає, що якщо висловлення (Х = 1) істинне, то « НЕ Х» (
» означає логічне заперечення і називається «інверсією». Вона означає, що якщо висловлення (Х = 1) істинне, то « НЕ Х» ( 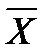 ) – хибне (
) – хибне ( 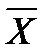 =0) і навпаки, якщо Х=0, то
=0) і навпаки, якщо Х=0, то
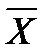 =1.
=1.
2. Логічна функціяY = f (x1, x2,…, xn) – це складне висловлення з кількох простих, які пов’язані між собою логічними операціями.
Логічна функція набуває значень 0 або 1 (Y  {0,1}).
{0,1}).
Однозначна функція Y = f (х) може бути зображена лише двома аргументами (0 і 1) і двома своїми значеннями (0 і 1). Отже число однозначних функцій у цьому випадку може бути 22 = 4.
Y = f (x)
3. Вхідний набір – це певна комбінація значень двійкових змінних Хі у логічній функції Y.
Y = f (x1,x2) – двозначна функція, тут число наборів аргументів 22 = 4 (  ,х1
,х1 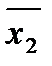 ,
, 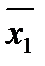 х2, х1х2).
х2, х1х2).
У випадку трьох змінних f(х1, х2, х3) наборів аргументів буде 23 = 8.
Логічна функція, яка має певні значення 0 або 1 на всіх вхідних наборах, називається повністю визначеною функцією. Якщо логічна функція має значення, які на деяких вхідних наборах не визначені, їх називають байдужими (або непевними).
Множину логічних функцій n-змінних можна утворити за допомогою трьох основних логічних операцій:
- логічного заперечення «  » - інверсії;
» - інверсії;
- логічного додавання «  » - диз’юнкції;
» - диз’юнкції;
- логічного множення «·» («  ») – кон’юнкції.
») – кон’юнкції.
Для цих операцій справедливі такі аксіоми (тотожності або правила):
1 · х = х;
1. Універсальна множина - 1  х = 1.
х = 1.
0 · х = 0;
2. Нульова множина - 0  х = х.
х = х.
х · х … = х;
3. Повторення (тавтологія) - х  х
х  … = х.
… = х.
х · 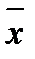 =0;
=0;
4. Доповнення - х 
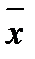 = 1.
= 1.
5. Подвійна інверсія - 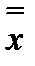 = х.
= х.


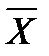 = 1,
= 1,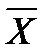 = 0.
= 0.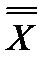 = Х.
= Х. » означає логічне заперечення і називається «інверсією». Вона означає, що якщо висловлення (Х = 1) істинне, то « НЕ Х» (
» означає логічне заперечення і називається «інверсією». Вона означає, що якщо висловлення (Х = 1) істинне, то « НЕ Х» (  {0,1}).
{0,1}). ,х1
,х1 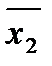 ,
, 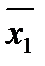 х2, х1х2).
х2, х1х2). » - диз’юнкції;
» - диз’юнкції; ») – кон’юнкції.
») – кон’юнкції.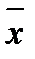 =0;
=0;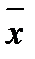 = 1.
= 1.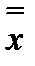 = х.
= х.