У цифрових та МП пристроях над двійковими числами виконуються як логічні, так і арифметичні операції.
Арифметичні операції (+,-,:,х) над двійковими числами реалізуються за допомогою спеціальних алгоритмів, які не використовуються у десятковій системі числення.
Додавання
0 + 0 = 0 10001111
0 + 1 = 1 111111
1 + 0 = 1 11001110
1 + 1 = 10
Пристрій, що виконує цю операцію – суматор.
Віднімання
0 – 0 = 0 11100011
1 – 0 = 1 10010110
10 – 1 = 1 01001101
1 – 1 = 0
Операцію віднімання можна замінити операцією додавання. Для цього від’ємне число зображують оберненим кодом +1, тобто доповняльним кодом.
А2 – В2 = А2 +  + 1 = А2 +
+ 1 = А2 + 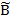 2
2
Якщо результат віднімання містить 1 у знаковому розряді, то ця сума отримана у доповняльному коді, якщо нуль – то в прямому коді.
Приклади. Знайти суму чисел:
1. А2 = 1010; В2 = -100
А2 = 0.1010 0.1010
В2 = 1.0100 → 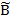 2 = 1.1011 + 1 = 1.1100 1.1100
2 = 1.1011 + 1 = 1.1100 1.1100
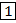 0.0110 - додатнє
0.0110 - додатнє
відкинути ↑
А2 + В2 = 110.
2. А2 = -1010; В2 = 100; 1.0110
А2 = 1.1010; В2 = 0.0100 0.0100
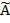 2 = 1.0101 + 1 = 1.0110;
2 = 1.0101 + 1 = 1.0110; 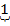 .1010
.1010
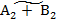 - 1 =
- 1 = 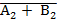 = 1.1010 – 1 = 1.1001 доповняльний код
= 1.1010 – 1 = 1.1001 доповняльний код
А2 + В2 = 1.0110 = -110
3. А2 = -1010; В2 = -100; 1.0110
А2 = 1.1010 → 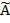 2 = 1.0110; 1.1100_
2 = 1.0110; 1.1100_
В2 = 1.0100 → 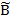 2 = 1.1100; 11.0010
2 = 1.1100; 11.0010
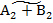 = 1.0010 →
= 1.0010 → 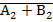 = 1.0010 – 1 = 1.0001;
= 1.0010 – 1 = 1.0001;
А2 + В2 = 1.1110 = -1110.
Множення.
Знаковий розряд отримують додаванням їх без врахування переносу.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0
Абсолютна величина добутку:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Приклад. 1.101
__0.10__
__101__
1.1010
Ділення
Знаковий розряд – як і при добутку.
Приклад.
11010111|_10110_
10110 1001,11
10110_
_10110_
10110_
010 ← залишок


 + 1 = А2 +
+ 1 = А2 + 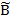 2
2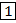 0.0110 - додатнє
0.0110 - додатнє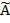 2 = 1.0101 + 1 = 1.0110;
2 = 1.0101 + 1 = 1.0110; 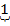 .1010
.1010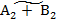 - 1 =
- 1 = 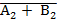 = 1.1010 – 1 = 1.1001 доповняльний код
= 1.1010 – 1 = 1.1001 доповняльний код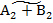 = 1.0010 →
= 1.0010 → 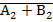 = 1.0010 – 1 = 1.0001;
= 1.0010 – 1 = 1.0001;