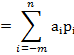У ЦТ використовується лише позиційна система числення (СЧ), за якою значення кожної цифри, що входить у число, залежить від місця її розташування у записі цього числа.
Кожна СЧ має певний набір символів (цифр), кількість символів в якому відповідає основі даної СЧ. Позиція символу у зображенні числа називається розрядом:
У загальному випадку будь-яке число А у позиційній системі числення з постійною основою Р можна відобразити числовим рядом
Ар= аn-1pn-1 +…+ a1p1 + a0p0 + a-1p-1 +…+ amp-m=
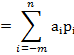
де n – число знаків до коми;
m – число знаків після коми;
ai – число в і-му розряді;
pi – вага і-го розряду.
У десятковій СЧ р=10 {0,1,2,…,8,9}.
А10 = 234,56710 = 2·102 + 3·101 + 4·100 + 5·10-1 + 6·10-2 + 7·10-3.
Двійкова СЧ має набір цифр {0,1}, тому р=2.
А2 = 101,1012 = 1·22 + 0·21 + 1·20 + 1·2-1 + 0·2-2 + 1·10-3 = 5,62510
Шістнадцяткова СЧ має набір цифр {0,1,2,…,9,A,B,C,D,E,F}, тому р=16.
А16 = 1ABF16 = 1·163 + 10·162 + 11·161 + 15·160 = 4096 + 2560 + 176 + 15 = 684710.
Вісімкова СЧ має набір цифр {0,1,…,7}, тому р=8.
А8 = 2368 = 2·82 + 3·81 + 6·80 = 15810.
Перетворення числової інформації
Перевід чисел з десяткової системи числення в інші.
А) З десяткової у двійкову:
12510 → 11111012
125|_2
124 62|_2_
1 6231|_2_
03015|_2_
1 14 7|_2_
1 63|_2_
1 1 1
Б) З десяткової у вісімкову:
32810 = 5108.
328|_8_
328 41|_8_
0 40 5
B) З десяткової у шістнадцяткову:
172710 = 6BF16.
1727|_16_
1712 107|_16_
15 96 6