Сплайн қисықтары.
Catmul-Room интерполяциялық қисығы. Элементар Бета сплайнды қисығы.
Өздерінің қасиеттерімен ерекшеленетін сплайндық қисықтардың әртүрлі варианттарының саны жетерлік. Солардың кейбіреулеріне тоқталып өтейік.
Catmull-Rom интерполяциялық қисығы
Catmull-Rom интерполяциялық қисығының берілген жиындағы Р0, Р1, Р2, Р3 нүктелері төмендегідей түрдегі теңдеудің көмегімен анықталады.
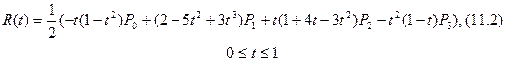

Catmull-Rom құрама сплайндық қисықтың қасиеттері:
· дәл тіреу (опорные) нүктесі арқылы өтеді;
· геометриялық үздіксіз болып табылады;
· негізгі функциялардың жиынтығы сонымен қатар қисықты анықтайды, яғни оның формасын ретке келтіруге (регулировка) мүмкіндігі жоқ.
Catmull-Rom сплайндық қисығы интерполяциялық болғандықтан, ол әрбір негізгі нүктелер арқылы өтеді.
Элементарлық Бета-сплайндық қисығы
Р0, Р1, Р2, Р3 нүктелер жиынынан тұратын Бета-сплайндық қисығы
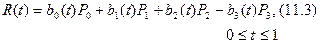
теңдеуімен өрнектеледі.
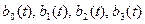 функционалдық коэффициенттері
функционалдық коэффициенттері
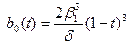
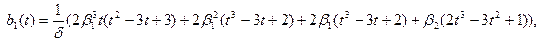
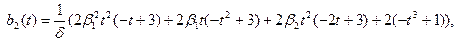
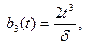 формулаларымен беріледі, мұнда
формулаларымен беріледі, мұнда 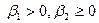 және
және 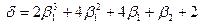 .
.
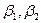 сандық параметрлері Бета – сплайндық қисық форманың параметрлері деп аталады.
сандық параметрлері Бета – сплайндық қисық форманың параметрлері деп аталады. 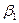 - параметром скоса(смещения) деп аталады, ал
- параметром скоса(смещения) деп аталады, ал 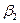 - параметром натяжения.
- параметром натяжения.
Құрама Бета-сплайндық қисықтың қасиеттері:
· геометриялық үздіксіз болып табылады;
· 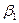 және
және 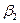 параметрлері қисық формасын басқарады.
параметрлері қисық формасын басқарады.
Бақылау сұрақтары.
- Catmull-Rom интерполяциялық қисығына анықтама?
- Catmull-Rom интерполяциялық қисығының қасиеттері?
- Элементарлық Бета-сплайндық қисығына анықтама?
- Элементарлық Бета-сплайндық қисығының қасиеттері?
ТАРАЗ ИННОВАЦИЯЛЫҚ ГУМАНИТАРЛЫҚ УНИВЕРСИТЕТІ
ЖАРАТЫЛЫСТАНУ ГУМАНИТАРЛЫҚ ФАКУЛЬТЕТІ
«ИНФОРМАТИКА ЖӘНЕ ЕСЕПТЕУ ТЕХНИКАСЫ» КАФЕДРАСЫ
«Компьютерлік графика» пәнінен зертханалық жұмыстарды орындауға арналған әдістемелік нұсқау
050602-«Информатика» мамандығына арналған
3 курс
Оқытушы: Байтуғанова А.О.
Зертханалық сабақтар: 45 сағат


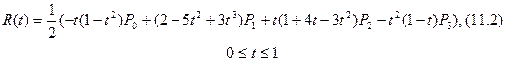

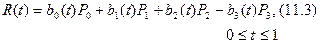
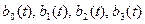 функционалдық коэффициенттері
функционалдық коэффициенттері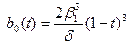
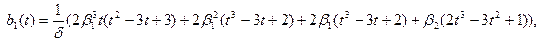
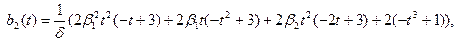
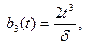 формулаларымен беріледі, мұнда
формулаларымен беріледі, мұнда 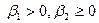 және
және 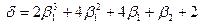 .
.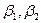 сандық параметрлері Бета – сплайндық қисық форманың параметрлері деп аталады.
сандық параметрлері Бета – сплайндық қисық форманың параметрлері деп аталады. 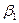 - параметром скоса(смещения) деп аталады, ал
- параметром скоса(смещения) деп аталады, ал 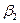 - параметром натяжения.
- параметром натяжения.