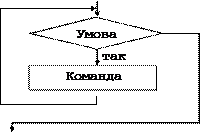| | | | | | |
| |  |
| |
| | |  |
| |
| | | | Поки < Умова>
вконати <Команда>
| |
| | | | 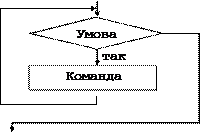 |
| |
Рис 1.8 Семантика команд управління
Блок-схема команди пояснює її виконання краще, ніж будь-який словесний опис.
Уявіть собі, однак, що Вам пропонують розглянути алгоритм, блок-схема якого зображена на рис 1.9.
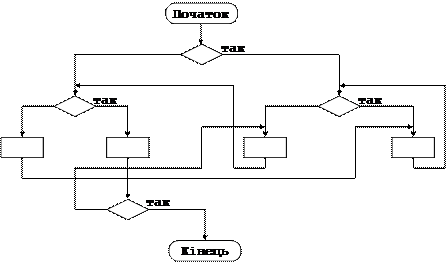
Рис 1.9. Блок-схема алгоритму типу «спагетті».
Автор алгоритму при цьому стверджує, що його алгоритм працює правильно, тобто завжди вирішує поставлену задачу.
Чи легко Вам буде розібратися в лабіринті переходів між блоками, і перевірити логіку обчислень? Звичайно, ні. Кожна послідовність дій тут так вплетена в інші можливі послідовності, що все це разом узяте нагадує ретельно перемішані спагетті.
З технічної точки зору причина утворення спагетті полягає в тому, що блок Умова має два виходи, які, у принципі, можна направляти куди завгодно. Більш важливим є те, що у нашого гіпотетичного автора не все в порядку з логікою мислення. Він не зумів виділити головні і допоміжні способи управління обчисленнями, не зумів структурувати алгоритм. Наявність же блоку Умова з його двома виходами дозволяє деяким чином скомбінувати переходи замість того, щоб направляти процес побудови алгоритму по шляху визначення логічно обґрунтованої структури управління.
Розглянемо алгоритм рішення наступної задачі:
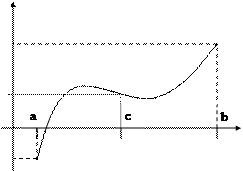
Приклад 1.6. Алгоритм наближеного розв’язання рівняння f(x) = 0 методом поділу відрізка навпіл.
У підручниках з обчислювальної математики цей метод розглядається як один з найбільш простих методів наближеного рішення рівнянь.
| | | | |
| |  | | | Дано:
Числовий відрізок [a, b].
Функція f(x), неперервна на відрізку і має на цьому відрізку єдиний корінь x0.
t – задана точність.
Знайти:
Корінь x0
| |
| |
Метод:
Відрізок [a, b] розділимо навпіл точкою с. Визначимо, на якій з половин відрізка - [a, с] або [с, b] знаходиться шуканий корінь. (Оскільки функція f(x) неперервна і корінь x0 єдиний, на кінцях відрізка, що містить x0, функція f(x) приймає протилежні за знаком значення.) Поділ відрізка навпіл будемо продовжувати доти, поки його довжина не стане менше, ніж задана точність t. Тоді наближеним значенням x0 можна вибрати середню точку цього відрізка.
Розробляючи алгоритм, спочатку визначимо його вхід і вихід:
Алгоритм Рівняння;
Вхід
a, b, t: ДІЙСН;
Вихід
X0: ДІЙСН;