Метод Монте-Карло є імовірнісним методом. За допомогою цього метода можна обчислити площу фігури, об’єм, розв'язати системи рівнянь, приблизно вирахувати значення числа π.
Метод Монте-Карло найчастіше застосовують при приблизному обчисленні площ геометричних фігур із точністю, достатньою для практики. Хоча відповідь при таких обчисленнях виходить кожного разу різною, але округлений результат завжди приблизно однаковий.
Суть цього методу в наступному. Припустимо, у нас є геометрична фігура довільної форми (мал.), площу якої необхідно обчислити. Опишемо навколо неї іншу фігуру, площу якої можна легко знайти, наприклад прямокутник із площею 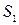 .
.
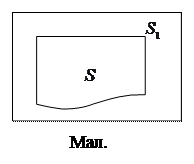 Уявимо, що площа прямокутника і площа нашої фігури рівномірно покриваються шаром снігу. В цьому випадку відношення кількості сніжинок, які впали в межах даної фігури
Уявимо, що площа прямокутника і площа нашої фігури рівномірно покриваються шаром снігу. В цьому випадку відношення кількості сніжинок, які впали в межах даної фігури 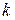 , до загальної кількості сніжинок
, до загальної кількості сніжинок 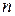 пропорційне площі даної фігури. Тоді можемо записати:
пропорційне площі даної фігури. Тоді можемо записати: 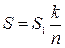 .
.
Тепер, якщо кількість сніжинок замінити точками, які отримані за допомогою генератора випадкових чисел, можна розв'язати будь-яку задачу з використанням метода Монте-Карло.
Приклад. Обчислити площу, обмежену графіками функцій: 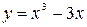 ,
, 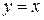 .
.
Інформаційна модель:
| Об’єкт
| Параметри
|
| Назва
| Значення
|
| Площа, обмежена графіками функцій
| Функції
| 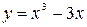
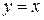
|
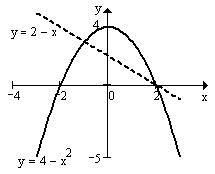
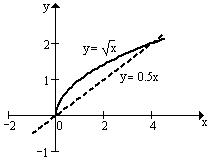
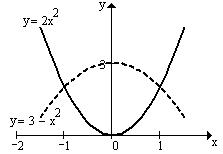
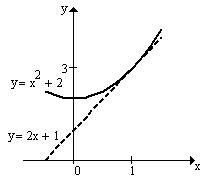
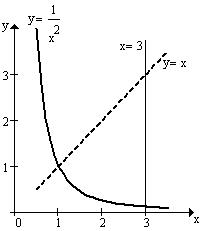
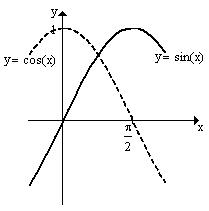
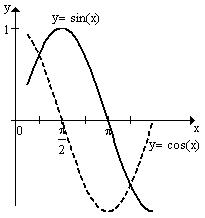
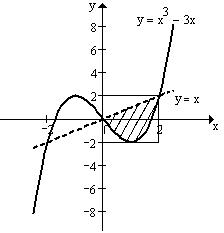 Побудуємо графіки даних функцій в одній системі координат. Ми бачимо, що обмежена цими графіками площа симетрична відносно початку координат, отже можна знайти значення площі праворуч від осі
Побудуємо графіки даних функцій в одній системі координат. Ми бачимо, що обмежена цими графіками площа симетрична відносно початку координат, отже можна знайти значення площі праворуч від осі 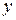 та помножити на 2. Дана область належить до проміжку: відносно осі
та помножити на 2. Дана область належить до проміжку: відносно осі 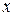 [0;2], та відносно осі
[0;2], та відносно осі 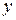 [-2;2]. Згідно з методом Монте-Карло опишемо навколо відповідної частини простору прямокутник з координатами вершин (0;-2), (0;2), (2;2), (2;-2).
[-2;2]. Згідно з методом Монте-Карло опишемо навколо відповідної частини простору прямокутник з координатами вершин (0;-2), (0;2), (2;2), (2;-2).
Розробка комп’ютерної моделі проводиться на морві програмування Pascal:
– в отриманий прямокутник «накидаємо» точок із випадковими значеннями координат. Нехай 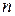 – загальна кількість точок (задається з клавіатури, чим вона більше, тим точніший результат), а
– загальна кількість точок (задається з клавіатури, чим вона більше, тим точніший результат), а 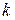 – кількість точок, що потрапили в область, обмежену графіками (початкове значення – 0).
– кількість точок, що потрапили в область, обмежену графіками (початкове значення – 0).
Функція random виводить випадкові значення чисел від 0 до 1, тому для того, щоб отримати числа із проміжку [0;2] необхідно помножити цю функцію на число 2. Якщо ж проміжок не починається з нуля, як наприклад наші значення по 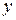 , то функцію random необхідно помножити на різницю кінців відрізка та додати менший з них.
, то функцію random необхідно помножити на різницю кінців відрізка та додати менший з них.
x:=2random;
y:=-2+(2-(-2))random;
– наступний крок – це перевірка, чи належить точка з отриманими випадковими координатами необхідній області. Так як графік функції 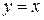 обмежує площу зверху, а
обмежує площу зверху, а 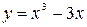 – знизу, то мають виконуватися наступні нерівності: y<=x,
– знизу, то мають виконуватися наступні нерівності: y<=x, 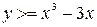 . Якщо вони виконуються, то ми додаємо до кількості точок, що потрапили в площину, ще одиницю.
. Якщо вони виконуються, то ми додаємо до кількості точок, що потрапили в площину, ще одиницю.
– операція проводиться 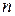 разів.
разів.
– розраховуємо площу прямокутника та, за формулою 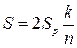 , розраховуємо значення площі, обмеженої графіками заданих функцій.
, розраховуємо значення площі, обмеженої графіками заданих функцій.
Нижче наведено текст програми для обчислення площі методом Монте-Карло, написаної на мові програмування Pascal:
program z1;
var x,y,S,Sp :real;
i,k,n:integer;
begin
Writeln('Vvedite n');
readln(n);
k:=0;
i:=1;
while i<=n do
begin
x:=random*2;
y:=-2+(2-(-2))*random;
if (y<=x) and (y>=x*x*x-3*x) then k:=k+1;
i:=i+1;
end;
Sp:=2*4;
S:=2*Sp*k/n;
writeln('S=',S);
end.
– Відповідь: 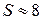 .
.
Завдання для самостійного виконання.
У наступних завданнях дані функції залежностей 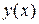 , графіки яких обмежують деякі площі, величини яких необхідно обчислити.
, графіки яких обмежують деякі площі, величини яких необхідно обчислити.
 1)
1) 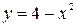 ,
, 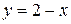 .
.
Формалізація задачі:
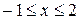 ;
; 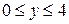 .
.
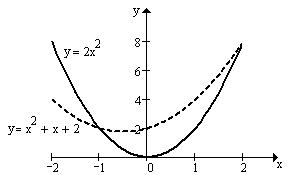 2)
2) 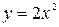 ,
, 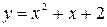 .
.
Формалізація задачі:
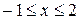 ;
; 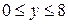 .
.
 3)
3) 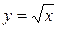 ,
, 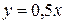 .
.
Формалізація задачі:
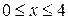 ;
; 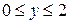 .
.
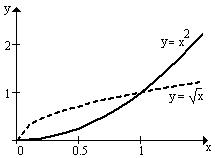 4)
4) 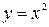 ,
, 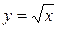 .
.
Формалізація задачі:
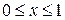 ;
; 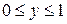 .
.
 5)
5) 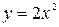 ,
, 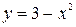 .
.
Формалізація задачі:
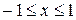 ;
; 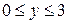 .
.
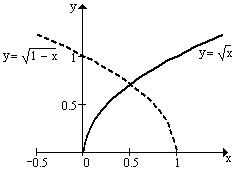 6)
6) 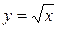 ,
, 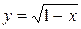 ,
, 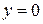 .
.
Формалізація задачі:
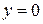 – це пряма, яка співпадає із віссю абсцис. У даному випадку простіше обчислити площу половини області, обмеженої графіками, а потім помножити її на 2. Тобто беремо
– це пряма, яка співпадає із віссю абсцис. У даному випадку простіше обчислити площу половини області, обмеженої графіками, а потім помножити її на 2. Тобто беремо 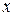 не від 0 до 1, а
не від 0 до 1, а 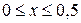 .
. 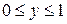 .
.
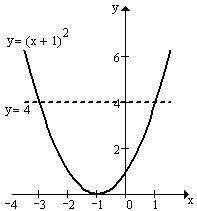 7)
7) 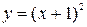 ,
, 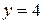 .
.
Формалізація задачі:
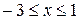 ;
; 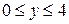 .
.
 8)
8) 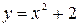 ,
, 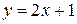 ,
, 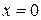 .
.
Формалізація задачі:
Графік функції 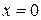 – це пряма яка співпадає із віссю ординат.
– це пряма яка співпадає із віссю ординат.
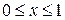 ;
; 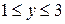 .
.
 9)
9) 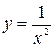 ,
, 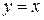 ,
, 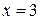 .
.
Формалізація задачі:
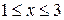 ;
; 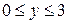 .
.
 10)
10) 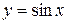 ,
, 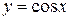 ,
, 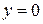 (
( 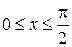 ).
).
Формалізація задачі:
У даному випадку простіше обчислити площу половини області обмеженої графіками, а потім помножити її на 2. Тобто беремо 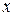 не від 0 до
не від 0 до 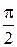 , а
, а 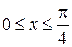 ,
, 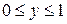 .
.
 11)
11) 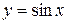 ,
, 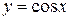 (
( 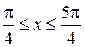 ).
).
Формалізація задачі:
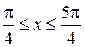 ;
; 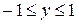 .
.
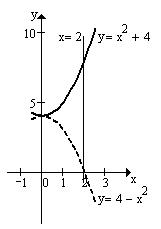 12)
12) 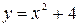 ,
, 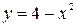 ,
, 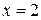 .
.
Формалізація задачі:
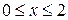 ;
; 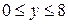 .
.
ЗМІСТ
1. Поняття моделі............................................................................................... 2
2. Класифікація моделей.................................................................................... 3
3. Основні етапи моделювання.......................................................................... 5
4. Похибки моделей........................................................................................... 7
5. Розробка і створення графічних моделей..................................................... 9
5.1 Засоби графічного редактора Paint......................................................... 9
5.1.1 Моделювання геометричних операцій і фігур............................... 9
5.1.2 Конструювання.............................................................................. 12
5.2 Моделі у вигляді блок-схем. Засоби векторної графіки текстового редактору Word.................................................................................................................. 15
6. Моделі у вигляді таблиць. Засоби середовища баз даних Access............. 20
7. Математичні моделі. Засоби електронних таблиць Excel. Система програмування......................................................................................................................... 25
7.1 Розв’язання задач за допомогою рекурентних співвідношень та створення масивів даних....................................................................................................... 26
7.2 Завдання на знаходження екстремумів................................................. 34
7.3 Задачі на використання методу кінцевих різниць (метод Ейлера)...... 42
7.4 Розрахунок площі методом Монте-Карло............................................ 55


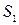 .
. Уявимо, що площа прямокутника і площа нашої фігури рівномірно покриваються шаром снігу. В цьому випадку відношення кількості сніжинок, які впали в межах даної фігури
Уявимо, що площа прямокутника і площа нашої фігури рівномірно покриваються шаром снігу. В цьому випадку відношення кількості сніжинок, які впали в межах даної фігури 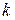 , до загальної кількості сніжинок
, до загальної кількості сніжинок 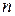 пропорційне площі даної фігури. Тоді можемо записати:
пропорційне площі даної фігури. Тоді можемо записати: 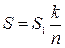 .
.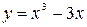 ,
, 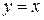 .
.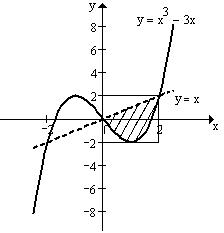 Побудуємо графіки даних функцій в одній системі координат. Ми бачимо, що обмежена цими графіками площа симетрична відносно початку координат, отже можна знайти значення площі праворуч від осі
Побудуємо графіки даних функцій в одній системі координат. Ми бачимо, що обмежена цими графіками площа симетрична відносно початку координат, отже можна знайти значення площі праворуч від осі 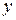 та помножити на 2. Дана область належить до проміжку: відносно осі
та помножити на 2. Дана область належить до проміжку: відносно осі 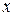 [0;2], та відносно осі
[0;2], та відносно осі 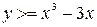 . Якщо вони виконуються, то ми додаємо до кількості точок, що потрапили в площину, ще одиницю.
. Якщо вони виконуються, то ми додаємо до кількості точок, що потрапили в площину, ще одиницю.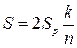 , розраховуємо значення площі, обмеженої графіками заданих функцій.
, розраховуємо значення площі, обмеженої графіками заданих функцій.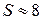 .
.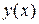 , графіки яких обмежують деякі площі, величини яких необхідно обчислити.
, графіки яких обмежують деякі площі, величини яких необхідно обчислити. 1)
1) 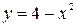 ,
, 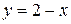 .
.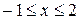 ;
; 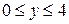 .
. 2)
2) 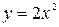 ,
, 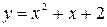 .
.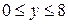 .
. 3)
3) 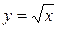 ,
, 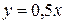 .
.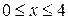 ;
; 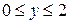 .
. 4)
4) 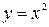 ,
, 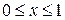 ;
; 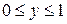 .
. 5)
5) 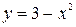 .
.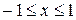 ;
; 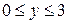 .
. 6)
6) 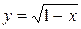 ,
, 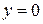 .
.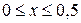 .
.  7)
7) 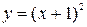 ,
, 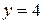 .
.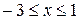 ;
;  8)
8) 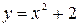 ,
, 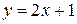 ,
, 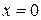 .
.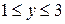 .
. 9)
9) 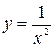 ,
, 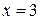 .
.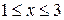 ;
;  10)
10) 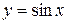 ,
, 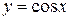 ,
, 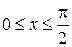 ).
).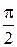 , а
, а 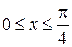 ,
,  11)
11) 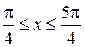 ).
).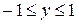 .
. 12)
12) 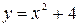 ,
, 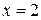 .
.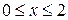 ;
;