Диференціальним рівнянням називається рівняння, яке містить, окрім функції 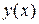 , ще і похідні
, ще і похідні 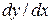 ,
, 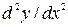 і т. д.. Диференціальні рівняння не входять до шкільного курсу математики, але їх можна розв’язувати використовуючи чисельні методи, зокрема елементи методу кінцевих різниць.
і т. д.. Диференціальні рівняння не входять до шкільного курсу математики, але їх можна розв’язувати використовуючи чисельні методи, зокрема елементи методу кінцевих різниць.
Розглянемо диференціальне рівняння першого порядку виду:
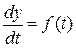 . (3.1)
. (3.1)
У загальному випадку аналітичного розв’язку (у вигляді формули) цього рівняння не існує. Чисельні методи дозволяють знайти розв’язок будь-якого рівняння. Однак відповідь виходить не у вигляді аналітичної залежності 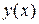 , тобто не у вигляді формули, а у вигляді рядів чисел:
, тобто не у вигляді формули, а у вигляді рядів чисел:
| x
| x1
| x2
| x3
| …
|
| y
| y1
| y2
| y3
| …
|
При цьому, обов’язково треба задати початкові умови.
Типовий метод чисельного розв’язку диференціальних рівнянь містить у собі перетворення диференціального рівняння в кінцево-різницеве. Припустимо, що при t=t0 функція y приймає значення y0. За цими початковими умовами, із рівняння (3.1), яке описує змінення функції y з часом, можна знайти наближене значення функції y в найближчій точці 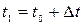 , якщо збільшення аргументу Δt мале. Припустимо, що швидкість змінення y на відрізку від t0до t1 постійна. У цьому випадку наближене значення функції y в точці
, якщо збільшення аргументу Δt мале. Припустимо, що швидкість змінення y на відрізку від t0до t1 постійна. У цьому випадку наближене значення функції y в точці 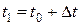 визначається виразом
визначається виразом
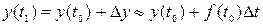 .
.
Ми можемо повторити цю процедуру ще раз і знайти значення y в точці 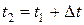 :
:
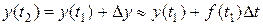 .
.
Це правило можна узагальнити і обчислити наближене значення функції в будь-якій точці 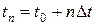 за ітераційною формулою:
за ітераційною формулою:
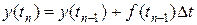 . (3.2)
. (3.2)
Даний метод називається методом дотичних, це метод Ейлера. Можна припустити, що метод даватиме гарне наближення до «істинного» значення функції y, якщо збільшення аргументу Δt досить мале. Ступінь «малості» Δt визначається вимогами певної задачі і тому може не конкретизуватися доти, поки метод не застосовується для вирішення конкретних задач.
У методі Ейлера передбачається, що швидкість змінення функції y на відрізку від tn-1 до tn постійна, а нахил дотичної обчислюється в початковій точці відрізку. Графічна інтерпретація виразу (3.2) приведена на малюнку.
Приклад. Кулька масою 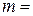 22 г і радіусом
22 г і радіусом 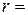 4,1 мм падає в олії, зустрічає силу опору
4,1 мм падає в олії, зустрічає силу опору 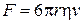 , де коефіцієнт в’язкості рідини η=0,95 кг/м·с. Необхідно знайти залежність швидкості, прискорення та шляху від часу падіння кульки.
, де коефіцієнт в’язкості рідини η=0,95 кг/м·с. Необхідно знайти залежність швидкості, прискорення та шляху від часу падіння кульки.
Інформаційна модель:
| Об’єкт
| Параметри
|
| Назва
| Значення
|
| Кулька
| Маса 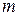 Радіус
Радіус 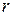
| 22 г
4,1 мм
|
| Олія
| Коефіцієнт в’язкості 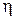
| 0,95 кг/м·с
|
На кульку діють сили: тяжіння, Архімеда 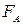 , опору олії
, опору олії 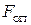 . За другим законом Ньютона отримуємо:
. За другим законом Ньютона отримуємо:

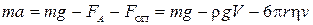 ,
,
де 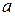 – прискорення руху тіла,
– прискорення руху тіла, 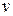 – швидкість руху тіла,
– швидкість руху тіла, 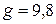 – прискорення вільного падіння,
– прискорення вільного падіння, 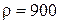 кг/м3 – густина олії,
кг/м3 – густина олії, 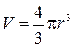 – об’єм кульки. Звідси одразу можна знайти прискорення:
– об’єм кульки. Звідси одразу можна знайти прискорення: 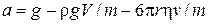 . За означенням:
. За означенням: 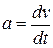 ,
, 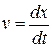 . Звідси знаходимо наступне співвідношення:
. Звідси знаходимо наступне співвідношення:
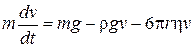 .
.
Ми отримали диференціальне рівняння. Для отримання точного розв’язку такого рівняння шкільного рівня математики не достатньо, але ми можемо розв’язати його приблизно за допомогою методу кінцевих різниць. Для цього замість нескінченно малого проміжку часу 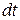 , розбиваємо весь час руху на деякі (скінченні) відрізки
, розбиваємо весь час руху на деякі (скінченні) відрізки 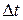 . І розглядаємо змінення швидкості та координати за кожен з цих відрізків:
. І розглядаємо змінення швидкості та координати за кожен з цих відрізків: 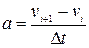 ,
, 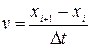 . Отримуємо наступні рекурентні співвідношення:
. Отримуємо наступні рекурентні співвідношення:
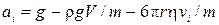
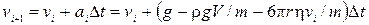 ,
,
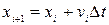 , де
, де 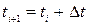 .
.
Розробка комп’ютерної моделі:
I спосіб розв’язання:
Початкові швидкість та координата дорівнюють нулю. Крок змінення часу візьмемо Δt = 0,2 с.
За допомогою електронних таблиць проводимо розрахунки та малюємо графіки залежностей швидкості, прискорення та координати від часу:
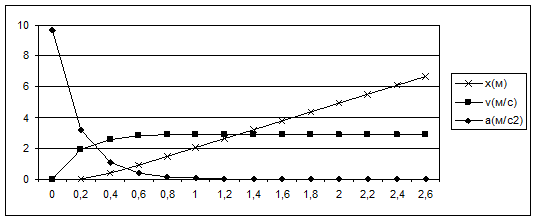
Ми бачимо, що через деякий час швидкість стає постійною, прискорення прямує до нуля, а графік змінення координати відповідає графіку рівномірного руху.
Звичайно, розроблена модель була б на багато точніша, якби крок за часом прямував до нуля. В цьому є похибка даної моделі. Спробуємо зменшити крок за часом до 0,1 с.
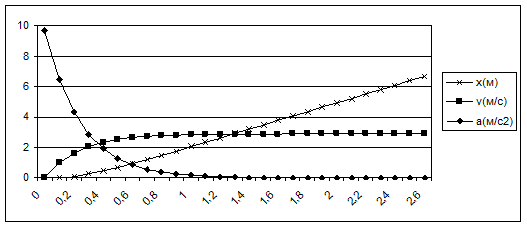
Бачимо, що графік став більш плавним. Тепер спробуємо збільшити крок до 0,4 с.
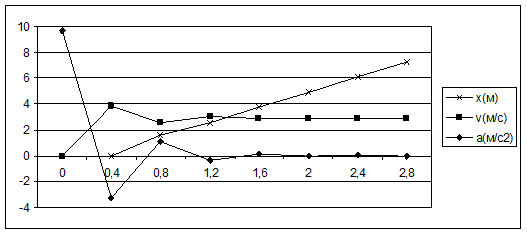
Цей графік вже набагато гірше ілюструє характер руху кульки.
II спосіб розв’язання:
При зозв’язанні задачі за допомогою мови програмування недоцільно виводити усі проміжні значення величини, що обчислюється, тому що при великому значенні 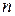 усі результати не вмістяться на екрані, тому виводимо тільки останні значення координати, швидкості та прискорення, що відповідають певному значенню часу
усі результати не вмістяться на екрані, тому виводимо тільки останні значення координати, швидкості та прискорення, що відповідають певному значенню часу 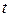 . Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми написаної на мові Pascal:
. Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми написаної на мові Pascal:
program z1;
var x,v,a,t,h,m,r,dt,etta,U:real;
i,n:integer;
begin
Writeln('Vvedite t');
readln(t);
Writeln('Vvedite n');
readln(n);
dt:=t/n;
m:=0.022;
r:=0.0041;
etta:=0.95;
U:=4/3*pi*r*r*r;
x:=0;
v:=0;
a:=9.8*(1-900*U/m);
i:=1;
while i<=n do
begin
x:=x+v*dt;
v:=v+a*dt;
{Час 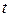 вводиться з клавіатури}
вводиться з клавіатури}
{ 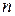 – кількість проміжків, на які поділяється час руху
– кількість проміжків, на які поділяється час руху 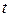 }
}
{ 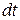 – крок за часом}
– крок за часом}
{η – коефіцієнт в’язкості олії}
{ 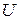 – об’єм кульки}
– об’єм кульки}
{Вводимо початкові значення координати, швидкості та прискорення}
{Вводимо цикл який послідовно розраховує значення 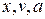 в залежності від часу.}
в залежності від часу.}
a:=a-6*pi*r*etta*v/m;
i:=i+1;
end;
writeln ('x=',x);
writeln ('v=',v);
writeln ('a=',a);
end.
{Виводимо результати}
Завдання для самостійного виконання
1) Падіння тіла. Тіло масою 70 кг падає у повітрі з великої висоти. Сила опору повітря 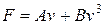 , де A = 5 Нс/м; B = 0,01 Нс3/м3. Знайти швидкість в залежності від часу.
, де A = 5 Нс/м; B = 0,01 Нс3/м3. Знайти швидкість в залежності від часу.
Формалізація задачі:
Візьмемо крок за часом Δt=0,2 с. Початкова швидкість v0=0 м/с.
За другим законом Ньютона:
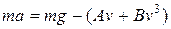 .
.
За означенням: 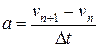 . Використовуючи це співвідношення записуємо:
. Використовуючи це співвідношення записуємо:
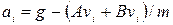 ;
;
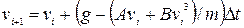 ;
;
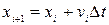 , де
, де 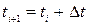 .
.
2) Електричне коло з індуктивністю. Електричне коло має індуктивність L=1 Гн та опір R=2 Ом, також має джерело струму з ЕРС ε=12 B. Встановити значення сили струму I в різні моменти часу після замикання кола. Намалювати графік залежності I(t).
Формалізація задачі:
В момент замикання кола струм в ньому відсутній. Під дією ЕРС джерела виникає струм, що зростає, і приводить до виникнення ЕРС самоіндукції, яка  напрямлена протилежно ЕРС джерела:
напрямлена протилежно ЕРС джерела: 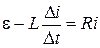 . За проміжок часу Δt струм змінюється на Δi:
. За проміжок часу Δt струм змінюється на Δi: 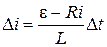 . Тепер, використовуючи метод кінцевих різниць, можна записати:
. Тепер, використовуючи метод кінцевих різниць, можна записати:
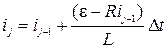 ,
, 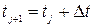 .
.
Початкове значення струму 0. 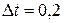 с.
с.
3) Падіння тіла з урахуванням сили опору. Пінопластова кулька радіусом 2,54 см і масою 0,000254 кг починає вертикальне падіння з висоти 4 метрів. Визначити силу, яка діє на кульку.
При розв’язанні цієї задачі необхідно розглянути три випадки: без урахування сили опору повітря; сила опору пропорційна швидкості; сила опору пропорційна квадрату швидкості. Побудувати графіки залежності y(t). Отримані залежності y(t) порівняти із експериментальними даними, що приведені у наступній таблиці. Коефіцієнт опору дорівнює k = 0,0001. Крок за часом 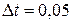 с.
с.
| t
|
| 0,132
| 0,23
| 0,332
| 0,432
| 0,532
| 0,632
| 0,732
| 0,832
| 0,932
|
| y
|
| 0,075
| 0,26
| 0,525
| 0,87
| 1,27
| 1,73
| 2,23
| 2,77
| 3,35
|
Формалізація задачі:
Для спрощення опису руху пінопластової кульки будемо розглядати її як матеріальну точку.
У початковий момент часу швидкість кульки дорівнює нулю. За визначенням:
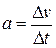 , звідки
, звідки 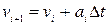 .
.
а) 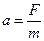 , де
, де 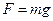 у тому випадку, коли ми нехтуємо силою опору повітря.
у тому випадку, коли ми нехтуємо силою опору повітря. 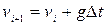 .
.
б) 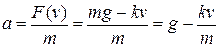 – сила опору пропорційна швидкості.
– сила опору пропорційна швидкості.
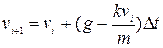 .
.
в) 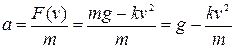 – сила опору пропорційна квадрату швидкості.
– сила опору пропорційна квадрату швидкості. 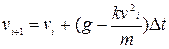 .
.
За означенням: 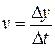 , тоді
, тоді 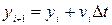 .
.
Необхідно обчислити 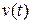 та
та 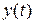 для трьох випадків.
для трьох випадків.
4) Чашка з кавою. Якою буде температура кави в чашці через час 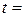 10, 15, 20 хвилин, якщо її початкова температура дорівнює 96˚С, а температура навколишнього середовища 22˚С.
10, 15, 20 хвилин, якщо її початкова температура дорівнює 96˚С, а температура навколишнього середовища 22˚С.
Формалізація задачі:
Природа переносу тепла від кави до навколишнього середовища в загальному випадку дуже складна й містить механізми конвекції, випромінювання, випаровування і теплопередачі. У тому випадку, коли різниця температур між об’єктом і навколишнім середовищем не дуже велика, швидкість змінення температури об’єкта можна вважати пропорційною цій різниці температур. Це твердження більш суворо можна сформулювати на мові диференціального рівняння:
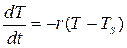 ,
,
де 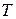 – температура кави,
– температура кави, 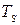 – температура навколишнього середовища, а
– температура навколишнього середовища, а 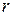 – коефіцієнт вистигання (
– коефіцієнт вистигання ( 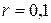 ). Дане співвідношення називається законом теплопровідності Ньютона.
). Дане співвідношення називається законом теплопровідності Ньютона.
За методом кінцевих різниці замінимо отримане диференційне рівняння рекурентним співвідношенням:
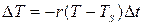 ;
;
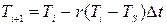 .
.
Крок за часом візьмемо 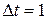 хвилина.
хвилина.
5) Зісковзування ланцюга. На столі лежить ланцюг, частина його звисає через край столу до низу. Загальна довжина ланцюга 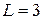 м, довжина частини, що звисає, дорівнює
м, довжина частини, що звисає, дорівнює 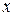 , загальна маса
, загальна маса 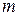 . Знайти час, за який ланцюг буде зісковзувати, якщо коефіцієнт тертя об стіл дорівнює
. Знайти час, за який ланцюг буде зісковзувати, якщо коефіцієнт тертя об стіл дорівнює 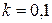 .
.
Формалізація задачі:
Маса частини ланцюга, що звисає, пропорційна відношенню довжини цієї частини до довжини всього ланцюга: 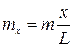 . І відповідно,
. І відповідно, 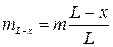 . За
. За 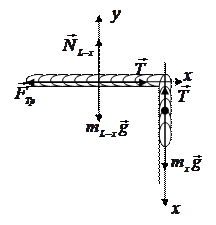 другим законом Ньютона запишемо рівняння руху окремо для двох частин ланцюга.
другим законом Ньютона запишемо рівняння руху окремо для двох частин ланцюга.
Частина, що лежить на столі: 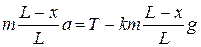 .
.
Частина, що звисає: 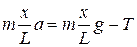 .
.
Із другого рівняння виразимо 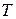 і підставимо в перше рівняння. Отримаємо
і підставимо в перше рівняння. Отримаємо
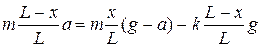 ,
,
виразимо 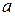
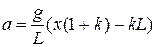 .
.
З останнього рівняння видно, що якщо 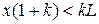 , то прискорення буде від’ємним, тобто ланцюг не з’їзжатиме. Тобто початкове значення координати має дорівнювати
, то прискорення буде від’ємним, тобто ланцюг не з’їзжатиме. Тобто початкове значення координати має дорівнювати 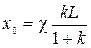 , де
, де 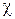 – деякий коефіцієнт, більший за одиницю.
– деякий коефіцієнт, більший за одиницю.
За означенням 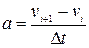 ,
, 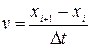 . Отже можемо записати співвідношення для швидкості та координати:
. Отже можемо записати співвідношення для швидкості та координати:
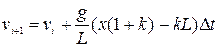 ;
;
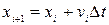 ;
;
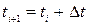 .
.
Нехай 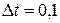 с,
с, 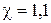 . Розрахунок проводити доки
. Розрахунок проводити доки 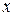 не буде дорівнювати
не буде дорівнювати 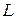 .
.
6) Падіння олівця. Скільки часу падатиме олівець довжиною 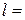 18 см, поставлений на вістря? Вважати, що олівець спочатку неминуче відхиляється від вертикалі. Кут відхилення дорівнює 1˚.
18 см, поставлений на вістря? Вважати, що олівець спочатку неминуче відхиляється від вертикалі. Кут відхилення дорівнює 1˚.
Формалізація задачі:
 Олівець падає, здійснюючи обертальний рух навколо вістря, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням
Олівець падає, здійснюючи обертальний рух навколо вістря, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням
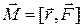 .
.
Модуль моменту сили дорівнюватиме:
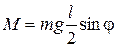 .
.
Із основного рівняння динаміки обертального руху запишемо:
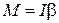 ,
,
де 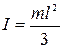 – момент інерції стрижня який, обертається навколо одного з кінців,
– момент інерції стрижня який, обертається навколо одного з кінців, 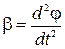 – кутове прискорення. Отже, отримуємо диференціальне рівняння:
– кутове прискорення. Отже, отримуємо диференціальне рівняння:
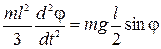 .
.
За означенням 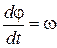 . Отримаємо систему рівнянь:
. Отримаємо систему рівнянь:
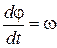 ,
, 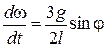 .
.
За допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень:
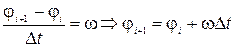 ;
;
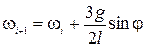 .
.
Крок за часом візьмемо 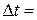 0,01 с, початкове значення кута
0,01 с, початкове значення кута 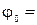 1˚. Обчислення проводити доки
1˚. Обчислення проводити доки 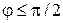 .
.
7) Гальмування колеса, що обертається на осі з рідкою змазкою. Колесо масою 1 кг, що рівномірно розподілена по ободу радіусом 0,35 м, обертається із кутовою швидкістю 10,5 рад/с на осі із рідкою змазкою і гальмується тільки тертям об вісь. Момент сил тертя дорівнює 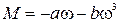 , де
, де 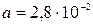 Н·м·с;
Н·м·с; 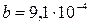 Н·м·с3. Колесо зупиняється, коли кутова швидкість стає рівною 0,1 рад/с. Знайдіть час та кількість обертів до зупинки.
Н·м·с3. Колесо зупиняється, коли кутова швидкість стає рівною 0,1 рад/с. Знайдіть час та кількість обертів до зупинки.
Формалізація задачі:
За умовою задачі момент сили тертя, яка гальмує колесо, дорівнює
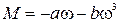 .
.
Із основного рівняння динаміки обертального руху запишемо:
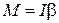 ,
,
де 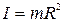 – момент інерції кільця, що обертається навколо осі, яка проходить через його центр,
– момент інерції кільця, що обертається навколо осі, яка проходить через його центр, 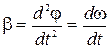 – кутове прискорення. Отже отримуємо систему двох диференціальних рівнянь:
– кутове прискорення. Отже отримуємо систему двох диференціальних рівнянь:
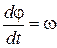 ;
; 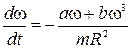 .
.
За допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень:
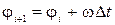 ;
;
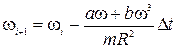 .
.
Крок за часом візьміть 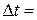 0,5 с. Обчислення проводити доти, доки
0,5 с. Обчислення проводити доти, доки 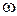 не буде дорівнювати 0,1 рад/с. Кількість обертів можемо знайти із співвідношення:
не буде дорівнювати 0,1 рад/с. Кількість обертів можемо знайти із співвідношення: 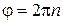 , де
, де 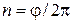 . Тут
. Тут 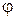 – це кінцеве значення кута.
– це кінцеве значення кута.
8) Падіння дерева. Визначити час падіння дерева, що знаходиться під кутом нахилу 10º відносно вертикалі. Висота дерева 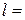 15 м.
15 м.
Формалізація задачі:
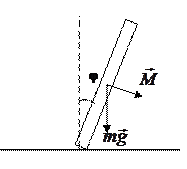 Дерево падає, здійснюючи обертальний рух навколо коренів, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням
Дерево падає, здійснюючи обертальний рух навколо коренів, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням
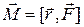 .
.
Модуль моменту сили дорівнюватиме:
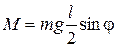 .
.
Із основного рівняння динаміки обертального руху запишемо:
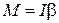 ,
,
де 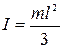 – момент інерції стрижня, який обертається навколо одного з кінців,
– момент інерції стрижня, який обертається навколо одного з кінців, 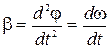 – кутове прискорення. Отримаємо систему двох диференціальних рівнянь:
– кутове прискорення. Отримаємо систему двох диференціальних рівнянь:
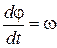 ,
, 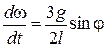 .
.
Так як 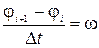 ,
, 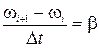 , то за допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень:
, то за допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень:
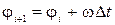 ;
;
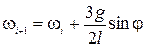 .
.
Крок за часом візьмемо 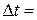 0,01 с, початкове значення кута
0,01 с, початкове значення кута 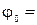 1˚. Обчислення проводити доки
1˚. Обчислення проводити доки 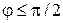 .
.
9) Рух потягу. На яку відстань за 3 хвилини від’їде від зупинки потяг масою 2000 тон, який веде тепловоз із силою тяги 25 Н? Дайте дві відповіді: без урахування і з урахуванням сили опору об повітря. 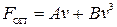 ,
, 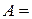 104 кг/с,
104 кг/с, 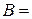 30 кг·с/м2.
30 кг·с/м2.
Формалізація задачі:
Необхідно розглянути два випадки: без урахування і з урахуванням сили опору.
1. Без урахування сили тертя.
Рух потягу зумовлений тільки силою тяги тепловоза. Отже за другим законом Ньютона:
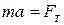 , звідки
, звідки 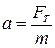 .
.
За означенням 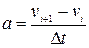 ,
, 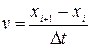 . Отримуємо
. Отримуємо
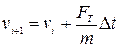 ;
;
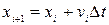 ,
,
де 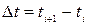 .
.
2. З урахуванням сили тертя.
За другим законом Ньютона:
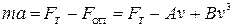 .
.
В цьому випадку прискорення залежить від швидкості:
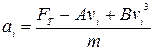 .
.
Аналогічно першому випадку запишемо співвідношення для швидкості та координати:
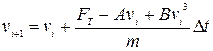 ;
;
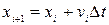 .
.
В обох випадках крок за часом взяти 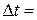 10 с. Обчислення проводити до
10 с. Обчислення проводити до 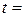 3 хвилини.
3 хвилини.
10) Старт ракети. Ракета масою 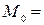 300 т стартує з Землі. Через який час вона віддалиться на 40 км, якщо кожну секунду відкидає 1000 кг продуктів згоряння із швидкістю
300 т стартує з Землі. Через який час вона віддалиться на 40 км, якщо кожну секунду відкидає 1000 кг продуктів згоряння із швидкістю 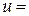 4000 м/с?
4000 м/с?
Формалізація задачі:
З часом ракета відкидає продукти згоряння, при цьому її маса зменшується, отже ракета є об’єктом зі змінною масою. Для опису руху такого об’єкту запишемо рівняння Мещерського:
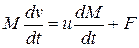 ,
,
де 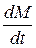 – швидкість змінення маси. Нехай
– швидкість змінення маси. Нехай 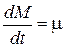 (за умовою вона дорівнює 1000 кг/с).
(за умовою вона дорівнює 1000 кг/с). 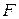 – це зовнішня сила, яка діє на ракету. Її знаходимо із закону всесвітнього тяжіння:
– це зовнішня сила, яка діє на ракету. Її знаходимо із закону всесвітнього тяжіння: 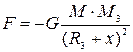 , де
, де 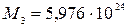 кг – маса Землі,
кг – маса Землі, 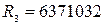 м – середній радіус Землі, і
м – середній радіус Землі, і 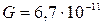 Н·м2/кг2 – гравітаційна стала. Знак мінус у законі всесвітнього тяжіння обумовлений тим, що сила напрямлена від ракети до Землі, тобто проти напрямку руху. Так як ракета відкидає продукти згоряння, то швидкість змінення маси від’ємна, і масу у даний момент часу можна знайти за формулою:
Н·м2/кг2 – гравітаційна стала. Знак мінус у законі всесвітнього тяжіння обумовлений тим, що сила напрямлена від ракети до Землі, тобто проти напрямку руху. Так як ракета відкидає продукти згоряння, то швидкість змінення маси від’ємна, і масу у даний момент часу можна знайти за формулою:
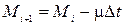 .
.
Із рівняння Мещерського за допомогою методу кінцевих різниць запишемо рекурентні співвідношення для швидкості та координати:
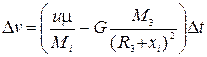 ,
,
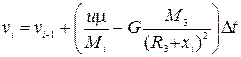 ;
;
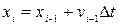 ,
,
де 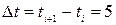 с. Початкове значення координати 0, початкове значення швидкості
с. Початкове значення координати 0, початкове значення швидкості 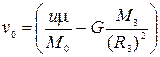 . Розрахунки проводити, доки координата не дорівнюватиме
. Розрахунки проводити, доки координата не дорівнюватиме 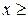 40000 м.
40000 м.
11) Рух трамваю. Трамвай розвиває силу тяги 1500 Н при масі 10 т. Сила опору дорівнює 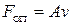 , де
, де 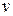 – швидкість;
– швидкість; 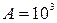 кг/с – коефіцієнт пропорційності. Через який час від початку руху можна вважати рух трамваю практично рівномірним? Яку відстань при цьому пройде трамвай, як буде змінюватися його швидкість з часом?
кг/с – коефіцієнт пропорційності. Через який час від початку руху можна вважати рух трамваю практично рівномірним? Яку відстань при цьому пройде трамвай, як буде змінюватися його швидкість з часом?
Формалізація задачі:
На трамвай діють дві сили: його власна сила тяги, та сила опору повітря. За другим законом Ньютона запишемо:
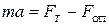 .
.
Звідки знайдемо прискорення:
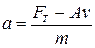 ,
,
бачимо, що прискорення залежить від швидкості. За означенням 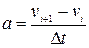 ,
, 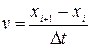 . Отже, згідно з методом кінцевих різниць, запишемо рекурентні співвідношення для розрахунку
. Отже, згідно з методом кінцевих різниць, запишемо рекурентні співвідношення для розрахунку 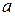 ,
, 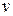 і
і 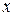 :
:
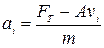 ;
;
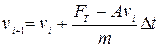 ;
;
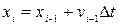 , де
, де 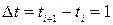 с.
с.
Побудуйте графіки залежності 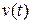 і
і 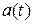 .
.
12) Математичний маятник. Вантаж на невагомому жорсткому підвісі довжиною 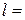 0,5 м коливається з великою амплітудою. Як буде змінюватися кутова швидкість впродовж одного періоду, якщо початкове значення кута
0,5 м коливається з великою амплітудою. Як буде змінюватися кутова швидкість впродовж одного періоду, якщо початкове значення кута 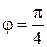 . Знайдіть період коливань.
. Знайдіть період коливань.
Формалізація задачі:
На вантаж, який здійснює обертальний рух навколо точки підвісу, діє сила тяжіння. Із означення моменту сили 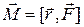 та із основного рівняння динаміки обертального руху
та із основного рівняння динаміки обертального руху 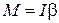 , де
, де 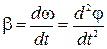 – кутове прискорення, а
– кутове прискорення, а 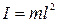 – момент інерції вантажу, що коливається на невагомому жорсткому підвісі. Запишемо рівняння руху маятника:
– момент інерції вантажу, що коливається на невагомому жорсткому підвісі. Запишемо рівняння руху маятника:
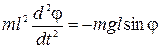 ,
,
Ми отримали диференцівльне рівняння другого порядку або систему двох диференційних рівнянь першого порядку:
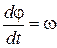 ,
, 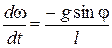
За допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень:
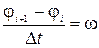 ,
, 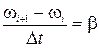 ;
;
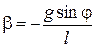 ;
;
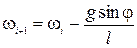 ;
;
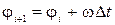 .
.
Крок за часом візьмемо 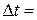 0,01 с, початкове значення кута
0,01 с, початкове значення кута 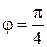 .
.


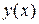 , ще і похідні
, ще і похідні 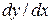 ,
, 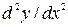 і т. д.. Диференціальні рівняння не входять до шкільного курсу математики, але їх можна розв’язувати використовуючи чисельні методи, зокрема елементи методу кінцевих різниць.
і т. д.. Диференціальні рівняння не входять до шкільного курсу математики, але їх можна розв’язувати використовуючи чисельні методи, зокрема елементи методу кінцевих різниць.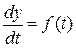 . (3.1)
. (3.1)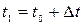 , якщо збільшення аргументу Δt мале. Припустимо, що швидкість змінення y на відрізку від t0до t1 постійна. У цьому випадку наближене значення функції y в точці
, якщо збільшення аргументу Δt мале. Припустимо, що швидкість змінення y на відрізку від t0до t1 постійна. У цьому випадку наближене значення функції y в точці 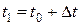 визначається виразом
визначається виразом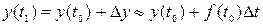 .
.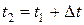 :
: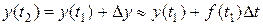 .
.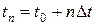 за ітераційною формулою:
за ітераційною формулою: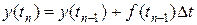 . (3.2)
. (3.2)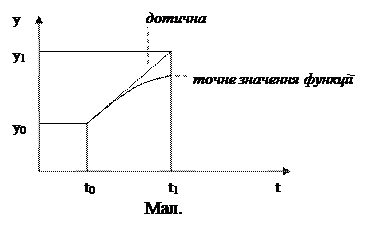
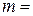 22 г і радіусом
22 г і радіусом 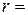 4,1 мм падає в олії, зустрічає силу опору
4,1 мм падає в олії, зустрічає силу опору 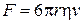 , де коефіцієнт в’язкості рідини η=0,95 кг/м·с. Необхідно знайти залежність швидкості, прискорення та шляху від часу падіння кульки.
, де коефіцієнт в’язкості рідини η=0,95 кг/м·с. Необхідно знайти залежність швидкості, прискорення та шляху від часу падіння кульки.
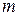 Радіус
Радіус 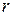
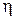
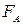 , опору олії
, опору олії 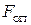 . За другим законом Ньютона отримуємо:
. За другим законом Ньютона отримуємо:
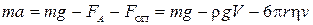 ,
,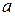 – прискорення руху тіла,
– прискорення руху тіла, 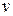 – швидкість руху тіла,
– швидкість руху тіла, 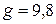 – прискорення вільного падіння,
– прискорення вільного падіння, 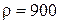 кг/м3 – густина олії,
кг/м3 – густина олії, 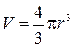 – об’єм кульки. Звідси одразу можна знайти прискорення:
– об’єм кульки. Звідси одразу можна знайти прискорення: 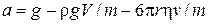 . За означенням:
. За означенням: 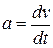 ,
, 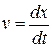 . Звідси знаходимо наступне співвідношення:
. Звідси знаходимо наступне співвідношення: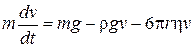 .
.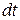 , розбиваємо весь час руху на деякі (скінченні) відрізки
, розбиваємо весь час руху на деякі (скінченні) відрізки 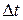 . І розглядаємо змінення швидкості та координати за кожен з цих відрізків:
. І розглядаємо змінення швидкості та координати за кожен з цих відрізків: 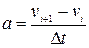 ,
, 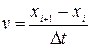 . Отримуємо наступні рекурентні співвідношення:
. Отримуємо наступні рекурентні співвідношення: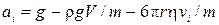
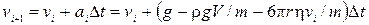 ,
,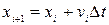 , де
, де 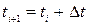 .
.


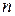 усі результати не вмістяться на екрані, тому виводимо тільки останні значення координати, швидкості та прискорення, що відповідають певному значенню часу
усі результати не вмістяться на екрані, тому виводимо тільки останні значення координати, швидкості та прискорення, що відповідають певному значенню часу 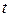 . Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми написаної на мові Pascal:
. Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми написаної на мові Pascal: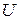 – об’єм кульки}
– об’єм кульки}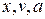 в залежності від часу.}
в залежності від часу.}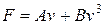 , де A = 5 Нс/м; B = 0,01 Нс3/м3. Знайти швидкість в залежності від часу.
, де A = 5 Нс/м; B = 0,01 Нс3/м3. Знайти швидкість в залежності від часу.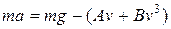 .
.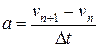 . Використовуючи це співвідношення записуємо:
. Використовуючи це співвідношення записуємо: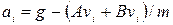 ;
;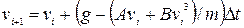 ;
; напрямлена протилежно ЕРС джерела:
напрямлена протилежно ЕРС джерела: 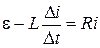 . За проміжок часу Δt струм змінюється на Δi:
. За проміжок часу Δt струм змінюється на Δi: 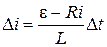 . Тепер, використовуючи метод кінцевих різниць, можна записати:
. Тепер, використовуючи метод кінцевих різниць, можна записати: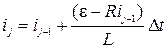 ,
, 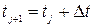 .
.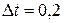 с.
с.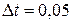 с.
с.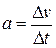 , звідки
, звідки 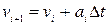 .
.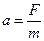 , де
, де 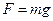 у тому випадку, коли ми нехтуємо силою опору повітря.
у тому випадку, коли ми нехтуємо силою опору повітря. 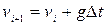 .
.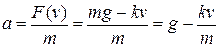 – сила опору пропорційна швидкості.
– сила опору пропорційна швидкості.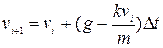 .
.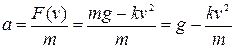 – сила опору пропорційна квадрату швидкості.
– сила опору пропорційна квадрату швидкості. 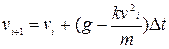 .
.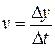 , тоді
, тоді 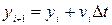 .
.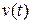 та
та 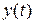 для трьох випадків.
для трьох випадків. 10, 15, 20 хвилин, якщо її початкова температура дорівнює 96˚С, а температура навколишнього середовища 22˚С.
10, 15, 20 хвилин, якщо її початкова температура дорівнює 96˚С, а температура навколишнього середовища 22˚С.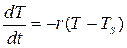 ,
,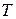 – температура кави,
– температура кави, 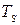 – температура навколишнього середовища, а
– температура навколишнього середовища, а 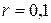 ). Дане співвідношення називається законом теплопровідності Ньютона.
). Дане співвідношення називається законом теплопровідності Ньютона.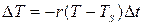 ;
;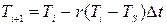 .
.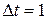 хвилина.
хвилина.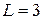 м, довжина частини, що звисає, дорівнює
м, довжина частини, що звисає, дорівнює 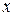 , загальна маса
, загальна маса 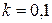 .
.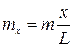 . І відповідно,
. І відповідно, 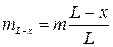 . За
. За  другим законом Ньютона запишемо рівняння руху окремо для двох частин ланцюга.
другим законом Ньютона запишемо рівняння руху окремо для двох частин ланцюга.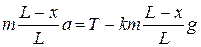 .
.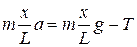 .
.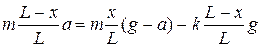 ,
,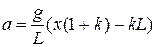 .
.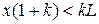 , то прискорення буде від’ємним, тобто ланцюг не з’їзжатиме. Тобто початкове значення координати має дорівнювати
, то прискорення буде від’ємним, тобто ланцюг не з’їзжатиме. Тобто початкове значення координати має дорівнювати 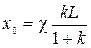 , де
, де 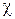 – деякий коефіцієнт, більший за одиницю.
– деякий коефіцієнт, більший за одиницю.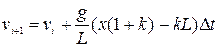 ;
;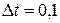 с,
с, 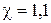 . Розрахунок проводити доки
. Розрахунок проводити доки 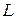 .
.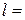 18 см, поставлений на вістря? Вважати, що олівець спочатку неминуче відхиляється від вертикалі. Кут відхилення дорівнює 1˚.
18 см, поставлений на вістря? Вважати, що олівець спочатку неминуче відхиляється від вертикалі. Кут відхилення дорівнює 1˚. Олівець падає, здійснюючи обертальний рух навколо вістря, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням
Олівець падає, здійснюючи обертальний рух навколо вістря, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням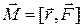 .
.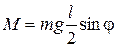 .
.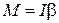 ,
,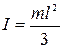 – момент інерції стрижня який, обертається навколо одного з кінців,
– момент інерції стрижня який, обертається навколо одного з кінців, 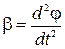 – кутове прискорення. Отже, отримуємо диференціальне рівняння:
– кутове прискорення. Отже, отримуємо диференціальне рівняння: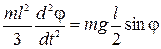 .
.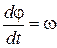 . Отримаємо систему рівнянь:
. Отримаємо систему рівнянь: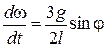 .
.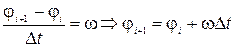 ;
;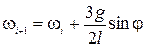 .
.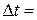 0,01 с, початкове значення кута
0,01 с, початкове значення кута 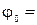 1˚. Обчислення проводити доки
1˚. Обчислення проводити доки 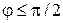 .
.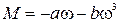 , де
, де 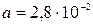 Н·м·с;
Н·м·с; 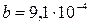 Н·м·с3. Колесо зупиняється, коли кутова швидкість стає рівною 0,1 рад/с. Знайдіть час та кількість обертів до зупинки.
Н·м·с3. Колесо зупиняється, коли кутова швидкість стає рівною 0,1 рад/с. Знайдіть час та кількість обертів до зупинки.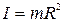 – момент інерції кільця, що обертається навколо осі, яка проходить через його центр,
– момент інерції кільця, що обертається навколо осі, яка проходить через його центр, 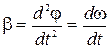 – кутове прискорення. Отже отримуємо систему двох диференціальних рівнянь:
– кутове прискорення. Отже отримуємо систему двох диференціальних рівнянь: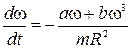 .
.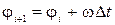 ;
;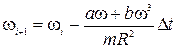 .
.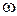 не буде дорівнювати 0,1 рад/с. Кількість обертів можемо знайти із співвідношення:
не буде дорівнювати 0,1 рад/с. Кількість обертів можемо знайти із співвідношення: 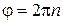 , де
, де 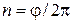 . Тут
. Тут 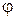 – це кінцеве значення кута.
– це кінцеве значення кута.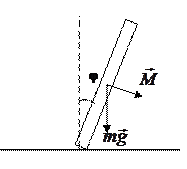 Дерево падає, здійснюючи обертальний рух навколо коренів, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням
Дерево падає, здійснюючи обертальний рух навколо коренів, за рахунок моменту сили тяжіння, яка діє на нього. Зо означенням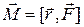 .
.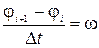 ,
, 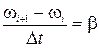 , то за допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень:
, то за допомогою методу кінцевих різниць перепишемо ці рівняння у вигляді рекурентних співвідношень: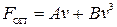 ,
,  104 кг/с,
104 кг/с,  30 кг·с/м2.
30 кг·с/м2.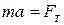 , звідки
, звідки 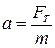 .
.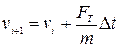 ;
;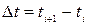 .
.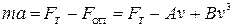 .
.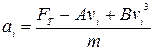 .
.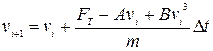 ;
;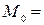 300 т стартує з Землі. Через який час вона віддалиться на 40 км, якщо кожну секунду відкидає 1000 кг продуктів згоряння із швидкістю
300 т стартує з Землі. Через який час вона віддалиться на 40 км, якщо кожну секунду відкидає 1000 кг продуктів згоряння із швидкістю 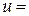 4000 м/с?
4000 м/с?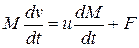 ,
,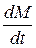 – швидкість змінення маси. Нехай
– швидкість змінення маси. Нехай 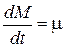 (за умовою вона дорівнює 1000 кг/с).
(за умовою вона дорівнює 1000 кг/с). 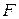 – це зовнішня сила, яка діє на ракету. Її знаходимо із закону всесвітнього тяжіння:
– це зовнішня сила, яка діє на ракету. Її знаходимо із закону всесвітнього тяжіння: 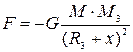 , де
, де 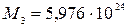 кг – маса Землі,
кг – маса Землі, 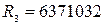 м – середній радіус Землі, і
м – середній радіус Землі, і 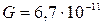 Н·м2/кг2 – гравітаційна стала. Знак мінус у законі всесвітнього тяжіння обумовлений тим, що сила напрямлена від ракети до Землі, тобто проти напрямку руху. Так як ракета відкидає продукти згоряння, то швидкість змінення маси від’ємна, і масу у даний момент часу можна знайти за формулою:
Н·м2/кг2 – гравітаційна стала. Знак мінус у законі всесвітнього тяжіння обумовлений тим, що сила напрямлена від ракети до Землі, тобто проти напрямку руху. Так як ракета відкидає продукти згоряння, то швидкість змінення маси від’ємна, і масу у даний момент часу можна знайти за формулою: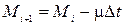 .
.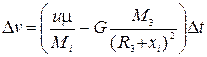 ,
,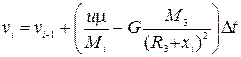 ;
;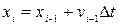 ,
,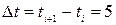 с. Початкове значення координати 0, початкове значення швидкості
с. Початкове значення координати 0, початкове значення швидкості 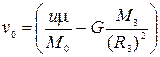 . Розрахунки проводити, доки координата не дорівнюватиме
. Розрахунки проводити, доки координата не дорівнюватиме 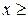 40000 м.
40000 м.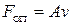 , де
, де 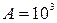 кг/с – коефіцієнт пропорційності. Через який час від початку руху можна вважати рух трамваю практично рівномірним? Яку відстань при цьому пройде трамвай, як буде змінюватися його швидкість з часом?
кг/с – коефіцієнт пропорційності. Через який час від початку руху можна вважати рух трамваю практично рівномірним? Яку відстань при цьому пройде трамвай, як буде змінюватися його швидкість з часом?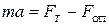 .
.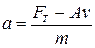 ,
,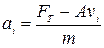 ;
;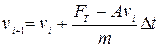 ;
;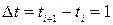 с.
с.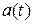 .
.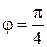 . Знайдіть період коливань.
. Знайдіть період коливань.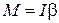 , де
, де 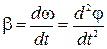 – кутове прискорення, а
– кутове прискорення, а 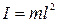 – момент інерції вантажу, що коливається на невагомому жорсткому підвісі. Запишемо рівняння руху маятника:
– момент інерції вантажу, що коливається на невагомому жорсткому підвісі. Запишемо рівняння руху маятника: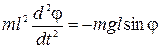 ,
,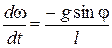
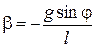 ;
;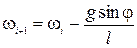 ;
;