Нехай функція 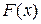 має максимум в деякій точці
має максимум в деякій точці 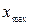 (мал.). Будемо розраховувати
(мал.). Будемо розраховувати 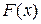 у трьох точках, що знаходяться одна від одної на відстанях
у трьох точках, що знаходяться одна від одної на відстанях 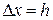 по
по 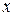 . Будемо рухатися по кривій
. Будемо рухатися по кривій 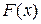 . Наявність екстремуму означає змінення знаку прирощення
. Наявність екстремуму означає змінення знаку прирощення 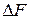 . Коли така трійка точок
. Коли така трійка точок 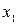 ,
, 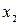 ,
, 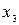 проходить через максимум або мінімум, добуток
проходить через максимум або мінімум, добуток 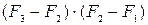 буде від’ємним. Тут необхідно зупинитися і прийняти значення
буде від’ємним. Тут необхідно зупинитися і прийняти значення 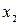 за наближене значення максимуму (мінімуму).
за наближене значення максимуму (мінімуму).
Приклад. Розрахунок геометричних параметрів об’єкта.
Маємо квадратний аркуш картону. Із аркуша по кутах вирізають чотири квадрати і склеюють коробку по сторонах вирізів. Яка має бути сторона вирізаного квадрату, щоб коробка мала найбільшу місткість?
Інформаційна модель:
| Об’єкт
| Параметри
|
| Назва
| Значення
|
| Аркуш картону
| Довжина сторони a
| 40 см
|
| Виріз
| Крок змінювання Δb
| 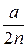
|
| Розмір b
| 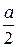
|
| Коробка
| Довжина сторони дна c
| 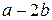
|
| Площа дна S
| 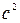
|
| Об’єм V
| 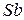
|
Розробка комп’ютерної моделі:
У представлених формулах а – довжина сторони картонного аркуша, b – розмір вирізу. Він змінюється від 0 до половини довжини сторони картонного аркуша через крок 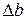 .
. 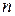 - величина розбиття відрізку (0;
- величина розбиття відрізку (0; 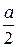 ), тобто кількість маленьких відрізків
), тобто кількість маленьких відрізків 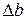 , на які ділиться цей проміжок.
, на які ділиться цей проміжок.
I спосіб розв’язання
Для моделювання будемо використовувати електронні таблиці. Інформаційна та математична моделі об’єднуються в таблицю, яка містить три області:
1. вихідні дані;
2. проміжні розрахунки;
3. результати.
– вводимо початкові дані;
– вводимо формули для розрахунків за правилами, прийнятими в середовищі електронних таблиць та проводимо розрахунки;
– отримуємо масив даних, тобто таблицю, яка відображає залежність об’єму коробки від розміру вирізу;
– за отриманими результатами будуємо графік залежності об’єму від довжини сторони вирізу.
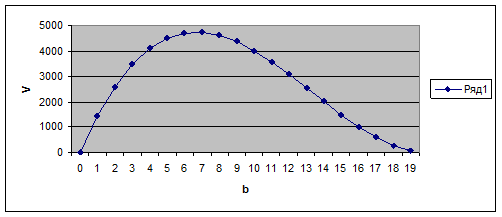
Максимум графіку буде співпадати із максимальним значенням об’єму коробки і відповідним до нього значенням довжини сторони вирізу.
II спосіб розв’язання:
Для моделювання будемо використовувати мову програмування Pascal. За умовою задачі нам необхідно знайти максимальне значення об’єму коробки та вивести значення 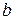 , яке відповідає цьому об’єму.
, яке відповідає цьому об’єму.
program extremum;
var b: array [0..255] of real;
S: array [0..255] of real;
V: array [0..255] of real;
c: array [0..255] of real;
l: array [0..255] of real;
db,a:real;
i,n:integer;
begin
writeln('Vvedite N');
readln(n);
a:=40;
b[0]:=0;
db:=a/(2*n);
For i:=1 to n do
b[i]:=b[i-1]+db;
For i:=0 to n do
begin
{Параметр 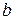 а також величини
а також величини 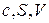 , які залежать від нього описуємо як масиви.}
, які залежать від нього описуємо як масиви.}
{З клавіатури вводимо значення розбиття відрізку (0; 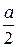 )
) 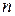 }
}
{Вводимо значення 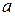 , та початкове значення
, та початкове значення 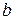 }
}
{ 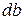 – це крок змінення довжини
– це крок змінення довжини 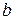 .}
.}
{розраховуємо та заносимо в пам’ять усі значення 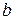 .}
.}
c[i]:=a-2*b[i];
S[i]:=c[i]*c[i];
V[i]:=S[i]*b[i];
end;
for i:=1 to n do
begin
l[i]:=(V[i+1]-V[i])*(V[i]-V[i-1]);
if l[i]<0 then
begin
writeln('b=', b[i]);
writeln('V=', V[i]);
end;
end;
end.
{Розраховуємо довжину сторони дна,
площу дна,
об’єм коробки.}
{Перевіряємо де знаходиться екстремум функції залежності 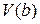 , тут
, тут 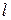 просто допоміжна змінна.}
просто допоміжна змінна.}
{Виводимо результати.}
Те, наскільки точним буде результат, напряму залежить від величини 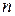 .
.
В таблиці приведені значення 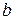 та
та 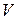 в залежності від
в залежності від 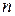 . Порівняйте їх із графіком, побудованим в Excel.
. Порівняйте їх із графіком, побудованим в Excel.
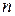
|
|
|
|
|
|
|
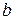
|
|
| 6,5
| 6,75
| 6,67
| 6,7
|
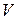
|
|
| 4738,5
| 4740,2
| 4740,7
| 4740,7
|
Завдання для самостійного виконання.
1) Довжини огорожі садової ділянки. Садова ділянка прямокутної форми має площу 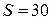 м2. При яких значеннях довжини та ширини ділянки довжина огорожі буде найменшою?
м2. При яких значеннях довжини та ширини ділянки довжина огорожі буде найменшою?
Формалізація задачі:
Нехай ширина дорівнює 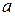 і змінюється від 1 до 30 із кроком 1 м, значення довжини ділянки знайдемо за формулою
і змінюється від 1 до 30 із кроком 1 м, значення довжини ділянки знайдемо за формулою 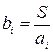 . Довжина огорожі дорівнюватиме периметру прямокутника, яким є садова ділянка, тобто довжину огорожі знайдемо за формулою:
. Довжина огорожі дорівнюватиме периметру прямокутника, яким є садова ділянка, тобто довжину огорожі знайдемо за формулою: 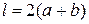 .
.
Необхідно знайти екстремум (мінімум) значення 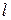 та вивести відповідні значення
та вивести відповідні значення 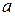 та
та 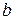 .
.
2) Площа трапеції. Знайти найбільшу площу рівнобедреної трапеції із периметром 4 та кутом при основі 45˚.
Формалізація задачі:
Площу трапеції можемо знайти за формулою:
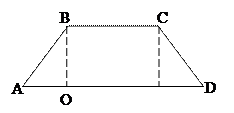
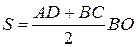 .
.
За умовою кут 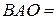 45˚, це означає, що прямокутний трикутник
45˚, це означає, що прямокутний трикутник 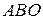 рівнобедрений:
рівнобедрений: 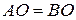 . Так як трапеція рівнобедрена, то
. Так як трапеція рівнобедрена, то 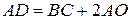 ,
, 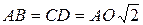 .
.
Підставимо усі ці співвідношення у формулу для периметра. Отримаємо
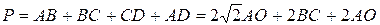 .
.
Виразимо 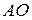 :
: 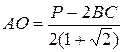 .
.
Після підстановки та нескладних математичних перетворень отримуємо
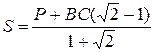 .
.
Довжина сторони 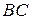 змінюється від 0 до напівпериметра (
змінюється від 0 до напівпериметра ( 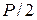 ).
).
3) Площа бокової поверхні циліндра. В круговий конус із радіусом основи 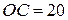 см та висотою
см та висотою 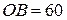 см вписано прямий круговий циліндр. При яких значеннях радіуса
см вписано прямий круговий циліндр. При яких значеннях радіуса 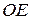 основи та висоти
основи та висоти 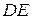 циліндра площа його бокової поверхні буде найбільшою?
циліндра площа його бокової поверхні буде найбільшою?
Формалізація задачі:
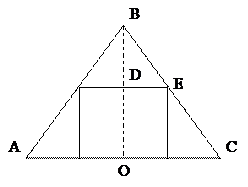 Розглянемо переріз конуса вздовж площини, яка містить його висоту.
Розглянемо переріз конуса вздовж площини, яка містить його висоту.
Площа бокової поверхні циліндра дорівнює добутку довжини кола основи на висоту: 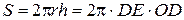
Із подібності трикутників 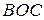 та
та 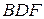 можемо записати:
можемо записати:
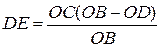 .
.
Підставимо це рівняння в рівняння для площини, отримаємо:
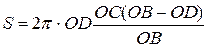 .
.
У цьому рівнянні змінною величиною залишається довжина висоти циліндра 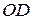 . Вона змінюється від 0 до
. Вона змінюється від 0 до 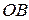 .
.
4) Відстань між автомобілями. Два автомобілі їдуть двома дорогами, що перетинаються під прямим кутом. Перший автомобіль знаходиться на відстані 3 км від перехрестя та його швидкість 40 км/год. Другий автомобіль знаходиться на відстані 5 км від перехрестя і його швидкість 60 км/год. В який момент відстань між автомобілями буде найменшою? Знайдіть цю відстань.
Формалізація задачі:
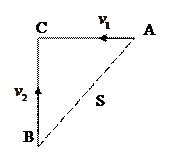 Відстань від кожного автомобіля до перехрестя дорівнює початковій відстані мінус відстань, яку вони пройшли за деякий час
Відстань від кожного автомобіля до перехрестя дорівнює початковій відстані мінус відстань, яку вони пройшли за деякий час 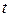 , тобто
, тобто
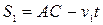 ,
, 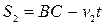 .
.
Відстань між автомобілями можна знайти за теоремою Піфагора:
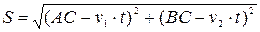 .
.
Час змінюється на проміжку від 0 до 10 хвилин. (Не забудьте перевести одиниці вимірювання в систему СІ).
5) Площа прямокутника. В заданий трикутник 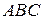 вписати прямокутник
вписати прямокутник 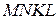 найбільшої площі так, щоб вершини
найбільшої площі так, щоб вершини 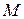 і
і 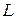 лежали на стороні
лежали на стороні 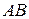 , а
, а 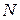 і
і 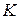 – на двох інших сторонах.
– на двох інших сторонах. 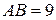 см,
см, 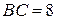 см,
см, 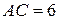 см.
см.
 Формалізація задачі:
Формалізація задачі:
Нехай висота, що опущена із вершини 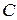 , дорівнює
, дорівнює 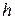 . Із малюнка бачимо, що
. Із малюнка бачимо, що 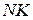 паралельне до
паралельне до 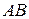 , з цього виходить що трикутники
, з цього виходить що трикутники 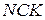 і
і 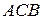 подібні. Із подібності трикутників маємо:
подібні. Із подібності трикутників маємо:
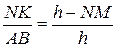 ;
;
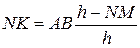 .
.
Отже площа прямокутника дорівнює:
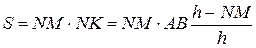 .
.
Висоту трикутника можемо знайти через його площу 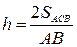 , де
, де 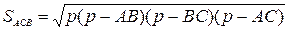 ,
, 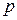 – напівпериметр трикутника. Довжина
– напівпериметр трикутника. Довжина 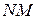 змінюється від 0 до
змінюється від 0 до 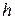 .
.
6) Об’єм конуса. Із кола радіусом 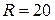 см вирізати розгортку конуса найбільшого об’єму.
см вирізати розгортку конуса найбільшого об’єму.
Формалізація задачі:
Щоб із кола можна було звернути конус, із нього необхідно вирізати сектор з деяким значенням центрального кута 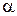 . Об’єм конуса дорівнює:
. Об’єм конуса дорівнює: 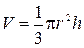 , де
, де 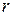 – радіус основи конуса, а
– радіус основи конуса, а 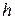 – його висота. Радіус основи можемо знайти через площу бокової поверхні конуса
– його висота. Радіус основи можемо знайти через площу бокової поверхні конуса 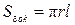 . Тут
. Тут 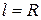 .
. 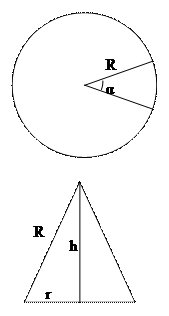 Також площу бокової поверхні конуса можна знайти як різницю площі кола та вирізаного сектора
Також площу бокової поверхні конуса можна знайти як різницю площі кола та вирізаного сектора 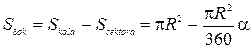 . Із двох останніх рівнянь знаходимо
. Із двох останніх рівнянь знаходимо 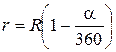 . Висоту конуса знаходимо за теоремою Піфагора:
. Висоту конуса знаходимо за теоремою Піфагора: 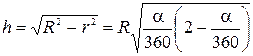 . Підставимо співвідношення для
. Підставимо співвідношення для 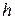 і
і 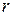 в формулу для об’єму. Отримаємо
в формулу для об’єму. Отримаємо
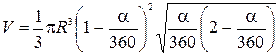 .
.
Значення кута змінюється від 0 до 360 градусів.
7) Об’єм циліндру. Знайти максимальний об'єм циліндра, вписаного в сферу радіусом 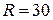 см.
см.
Формалізація задачі:
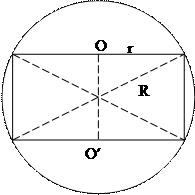 Розглянемо переріз сфери із вписаним циліндром вздовж площини, що містить вісь циліндра. Отримуємо прямокутник, вписаний в коло.
Розглянемо переріз сфери із вписаним циліндром вздовж площини, що містить вісь циліндра. Отримуємо прямокутник, вписаний в коло. 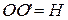 – висота циліндра. Кожна з діагоналей цього прямокутника дорівнює двом радіусам кола (радіус кола дорівнює радіусу сфери). Радіус основи циліндра знайдемо за теоремою Піфагора:
– висота циліндра. Кожна з діагоналей цього прямокутника дорівнює двом радіусам кола (радіус кола дорівнює радіусу сфери). Радіус основи циліндра знайдемо за теоремою Піфагора: 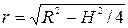 . Отже об’єм дорівнює
. Отже об’єм дорівнює
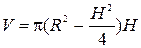 ,
,
де 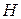 змінюється від 0 до
змінюється від 0 до 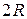 .
.
8) Площа ділянки. Парканом довжиною 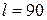 м необхідно обгородити ділянку, що має форму прямокутника із півколом, що прилягає до нього, діаметром півкола є одна із сторін прямокутника. Знайти найбільше значення площі такої ділянки.
м необхідно обгородити ділянку, що має форму прямокутника із півколом, що прилягає до нього, діаметром півкола є одна із сторін прямокутника. Знайти найбільше значення площі такої ділянки.
Формалізація задачі:
Площа ділянки такої форми дорівнює сумі площ прямокутника 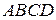 та півкола із діаметром
та півкола із діаметром 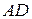 :
:
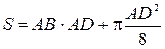 .
.
 Виразимо
Виразимо 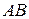 через периметр (
через периметр ( 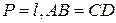 ):
):
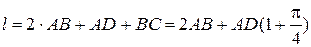 ;
;
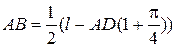 .
.
Після підстановки та спрощення отримаємо:
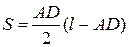 .
.
Якщо в співвідношенні для периметра взяти 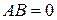 , то можна знайти найбільше можливе значення
, то можна знайти найбільше можливе значення 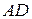 :
: 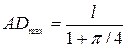 . Найменше можливе значення вказаної сторони дорівнює 0.
. Найменше можливе значення вказаної сторони дорівнює 0.
9) Площа прямокутника. Маємо дріт довжиною 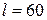 см. Необхідно зігнути його таким чином, щоб отримати прямокутник з найбільшою можливою площею.
см. Необхідно зігнути його таким чином, щоб отримати прямокутник з найбільшою можливою площею.
Формалізація задачі:
Нехай довжини сторін прямокутника 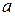 і
і 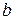 . Площа дорівнює добутку:
. Площа дорівнює добутку: 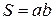 . Через периметр (
. Через периметр ( 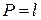 ) виразимо
) виразимо 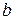 :
:
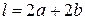 ;
;
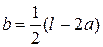 ;
;
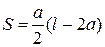 .
.
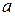 змінюється від 0 до
змінюється від 0 до 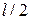 .
.
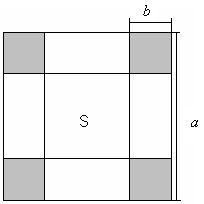
10) Площа квадрата. Маємо квадрат 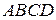 із стороною 5 см. Від його вершин відкладено рівні відрізки
із стороною 5 см. Від його вершин відкладено рівні відрізки 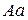 ,
, 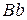 ,
, 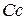 ,
, 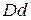 та точки
та точки 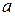 ,
, 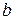 ,
, 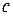 ,
, 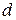 поєднані прямими. При якому значенні
поєднані прямими. При якому значенні 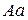 площа квадрату
площа квадрату 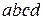 буде найменшою?
буде найменшою?
Формалізація задачі:
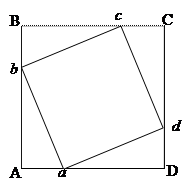 Нехай відстань
Нехай відстань 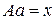 , тоді відстань
, тоді відстань 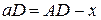 . За умовою
. За умовою 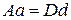 . Отже ми можемо знайти сторону
. Отже ми можемо знайти сторону 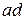 вписаного квадрата за теоремою Піфагора:
вписаного квадрата за теоремою Піфагора:
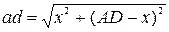 .
.
Тоді площа вписаного квадрата дорівнюватиме
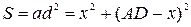 ,
,
де 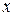 змінюється від 0 до
змінюється від 0 до 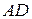 .
.
11) Відстані між пароплавом і яхтою. Із точок 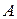 і
і 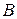 в напрямках, вказаних на малюнку вийшли одночасно пароплав і яхта. Їх швидкості відповідно дорівнюють
в напрямках, вказаних на малюнку вийшли одночасно пароплав і яхта. Їх швидкості відповідно дорівнюють 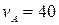 км/год.,
км/год., 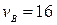 км/год.. Через який час відстань між ними буде найменшою, якщо
км/год.. Через який час відстань між ними буде найменшою, якщо 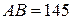 км?
км?
Формалізація задачі:
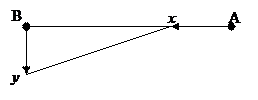
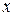 і
і 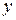 – це відстані пароплава та яхти від точки
– це відстані пароплава та яхти від точки 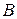 . У даний момент часу пароплав проплив відстань
. У даний момент часу пароплав проплив відстань 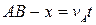 від початкового положення, а яхта пройшла шлях
від початкового положення, а яхта пройшла шлях 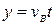 .
.
Отже за теоремою Піфагора можемо знайти відстань між пароплавом і яхтою:
 ,
,
Час змінюється від 0 до 10 хвилин.
12) Об’єм конуса. В кулю даного радіуса 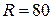 см вписати прямий круговий конус найбільшого об’єму.
см вписати прямий круговий конус найбільшого об’єму.
Формалізація задачі:
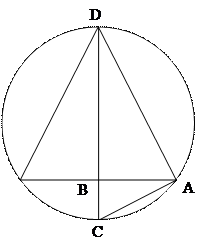 Об’єм конуса дорівнює
Об’єм конуса дорівнює 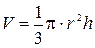 .
.
Розглянемо плоску фігуру: трикутник вписаний в коло. Тут 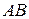 – радіус основи конуса, а
– радіус основи конуса, а 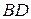 – висота (
– висота ( 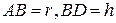 ). Зробимо допоміжні побудови і домалюємо кут
). Зробимо допоміжні побудови і домалюємо кут 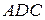 до трикутника. Бачимо, що цей трикутник прямокутний, а відрізок
до трикутника. Бачимо, що цей трикутник прямокутний, а відрізок 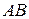 є висотою цього трикутника.
є висотою цього трикутника. 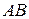 ділить
ділить 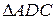 на два подібні прямокутні трикутники
на два подібні прямокутні трикутники 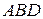 і
і 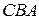 . Отже можемо записати
. Отже можемо записати 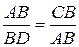 , звідки
, звідки 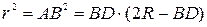 . Знаходимо об’єм
. Знаходимо об’єм
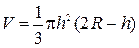 ,
,
де 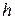 змінюється від 0 до
змінюється від 0 до 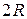 .
.


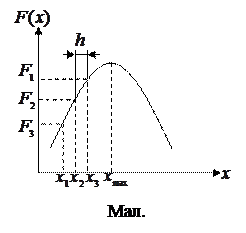
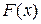 має максимум в деякій точці
має максимум в деякій точці 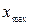 (мал.). Будемо розраховувати
(мал.). Будемо розраховувати 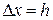 по
по 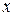 . Будемо рухатися по кривій
. Будемо рухатися по кривій 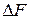 . Коли така трійка точок
. Коли така трійка точок 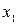 ,
, 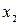 ,
, 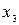 проходить через максимум або мінімум, добуток
проходить через максимум або мінімум, добуток 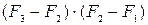 буде від’ємним. Тут необхідно зупинитися і прийняти значення
буде від’ємним. Тут необхідно зупинитися і прийняти значення 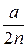
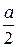
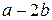
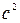
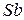

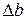 .
. 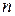 - величина розбиття відрізку (0;
- величина розбиття відрізку (0; 
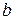 , яке відповідає цьому об’єму.
, яке відповідає цьому об’єму.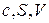 , які залежать від нього описуємо як масиви.}
, які залежать від нього описуємо як масиви.}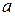 , та початкове значення
, та початкове значення 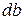 – це крок змінення довжини
– це крок змінення довжини 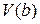 , тут
, тут 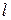 просто допоміжна змінна.}
просто допоміжна змінна.}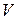 в залежності від
в залежності від 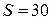 м2. При яких значеннях довжини та ширини ділянки довжина огорожі буде найменшою?
м2. При яких значеннях довжини та ширини ділянки довжина огорожі буде найменшою?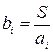 . Довжина огорожі дорівнюватиме периметру прямокутника, яким є садова ділянка, тобто довжину огорожі знайдемо за формулою:
. Довжина огорожі дорівнюватиме периметру прямокутника, яким є садова ділянка, тобто довжину огорожі знайдемо за формулою: 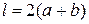 .
.
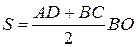 .
.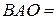 45˚, це означає, що прямокутний трикутник
45˚, це означає, що прямокутний трикутник 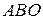 рівнобедрений:
рівнобедрений: 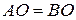 . Так як трапеція рівнобедрена, то
. Так як трапеція рівнобедрена, то 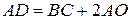 ,
, 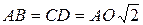 .
.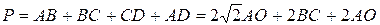 .
.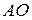 :
: 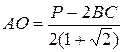 .
.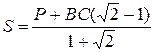 .
.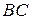 змінюється від 0 до напівпериметра (
змінюється від 0 до напівпериметра ( 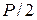 ).
).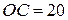 см та висотою
см та висотою 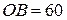 см вписано прямий круговий циліндр. При яких значеннях радіуса
см вписано прямий круговий циліндр. При яких значеннях радіуса 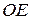 основи та висоти
основи та висоти 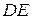 циліндра площа його бокової поверхні буде найбільшою?
циліндра площа його бокової поверхні буде найбільшою? Розглянемо переріз конуса вздовж площини, яка містить його висоту.
Розглянемо переріз конуса вздовж площини, яка містить його висоту.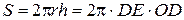
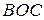 та
та 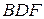 можемо записати:
можемо записати: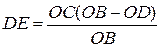 .
.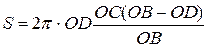 .
.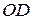 . Вона змінюється від 0 до
. Вона змінюється від 0 до  .
.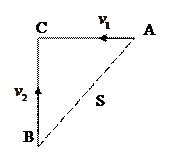 Відстань від кожного автомобіля до перехрестя дорівнює початковій відстані мінус відстань, яку вони пройшли за деякий час
Відстань від кожного автомобіля до перехрестя дорівнює початковій відстані мінус відстань, яку вони пройшли за деякий час 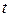 , тобто
, тобто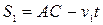 ,
, 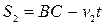 .
.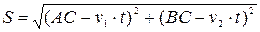 .
.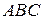 вписати прямокутник
вписати прямокутник 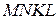 найбільшої площі так, щоб вершини
найбільшої площі так, щоб вершини 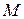 і
і 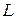 лежали на стороні
лежали на стороні 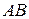 , а
, а 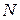 і
і 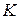 – на двох інших сторонах.
– на двох інших сторонах. 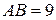 см,
см, 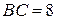 см,
см, 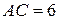 см.
см. Формалізація задачі:
Формалізація задачі: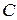 , дорівнює
, дорівнює 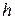 . Із малюнка бачимо, що
. Із малюнка бачимо, що 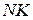 паралельне до
паралельне до 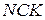 і
і 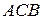 подібні. Із подібності трикутників маємо:
подібні. Із подібності трикутників маємо: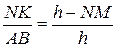 ;
;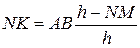 .
.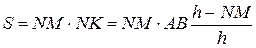 .
.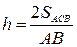 , де
, де 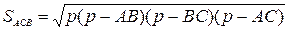 ,
, 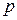 – напівпериметр трикутника. Довжина
– напівпериметр трикутника. Довжина 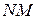 змінюється від 0 до
змінюється від 0 до 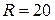 см вирізати розгортку конуса найбільшого об’єму.
см вирізати розгортку конуса найбільшого об’єму.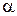 . Об’єм конуса дорівнює:
. Об’єм конуса дорівнює: 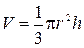 , де
, де 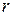 – радіус основи конуса, а
– радіус основи конуса, а 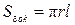 . Тут
. Тут 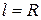 .
.  Також площу бокової поверхні конуса можна знайти як різницю площі кола та вирізаного сектора
Також площу бокової поверхні конуса можна знайти як різницю площі кола та вирізаного сектора 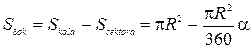 . Із двох останніх рівнянь знаходимо
. Із двох останніх рівнянь знаходимо 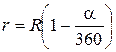 . Висоту конуса знаходимо за теоремою Піфагора:
. Висоту конуса знаходимо за теоремою Піфагора: 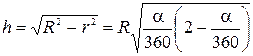 . Підставимо співвідношення для
. Підставимо співвідношення для 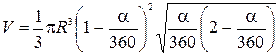 .
.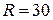 см.
см. Розглянемо переріз сфери із вписаним циліндром вздовж площини, що містить вісь циліндра. Отримуємо прямокутник, вписаний в коло.
Розглянемо переріз сфери із вписаним циліндром вздовж площини, що містить вісь циліндра. Отримуємо прямокутник, вписаний в коло. 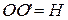 – висота циліндра. Кожна з діагоналей цього прямокутника дорівнює двом радіусам кола (радіус кола дорівнює радіусу сфери). Радіус основи циліндра знайдемо за теоремою Піфагора:
– висота циліндра. Кожна з діагоналей цього прямокутника дорівнює двом радіусам кола (радіус кола дорівнює радіусу сфери). Радіус основи циліндра знайдемо за теоремою Піфагора: 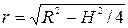 . Отже об’єм дорівнює
. Отже об’єм дорівнює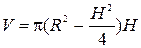 ,
,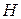 змінюється від 0 до
змінюється від 0 до 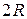 .
.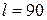 м необхідно обгородити ділянку, що має форму прямокутника із півколом, що прилягає до нього, діаметром півкола є одна із сторін прямокутника. Знайти найбільше значення площі такої ділянки.
м необхідно обгородити ділянку, що має форму прямокутника із півколом, що прилягає до нього, діаметром півкола є одна із сторін прямокутника. Знайти найбільше значення площі такої ділянки.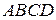 та півкола із діаметром
та півкола із діаметром 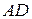 :
: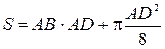 .
. Виразимо
Виразимо 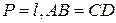 ):
):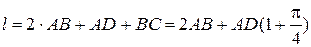 ;
;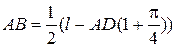 .
.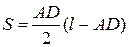 .
.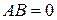 , то можна знайти найбільше можливе значення
, то можна знайти найбільше можливе значення 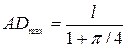 . Найменше можливе значення вказаної сторони дорівнює 0.
. Найменше можливе значення вказаної сторони дорівнює 0.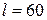 см. Необхідно зігнути його таким чином, щоб отримати прямокутник з найбільшою можливою площею.
см. Необхідно зігнути його таким чином, щоб отримати прямокутник з найбільшою можливою площею.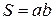 . Через периметр (
. Через периметр ( 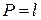 ) виразимо
) виразимо 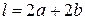 ;
;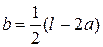 ;
;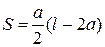 .
.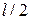 .
.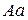 ,
, 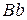 ,
, 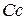 ,
, 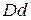 та точки
та точки 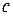 ,
, 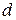 поєднані прямими. При якому значенні
поєднані прямими. При якому значенні 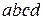 буде найменшою?
буде найменшою? Нехай відстань
Нехай відстань 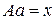 , тоді відстань
, тоді відстань 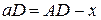 . За умовою
. За умовою 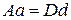 . Отже ми можемо знайти сторону
. Отже ми можемо знайти сторону 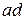 вписаного квадрата за теоремою Піфагора:
вписаного квадрата за теоремою Піфагора: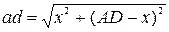 .
.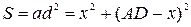 ,
,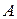 і
і 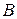 в напрямках, вказаних на малюнку вийшли одночасно пароплав і яхта. Їх швидкості відповідно дорівнюють
в напрямках, вказаних на малюнку вийшли одночасно пароплав і яхта. Їх швидкості відповідно дорівнюють 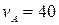 км/год.,
км/год., 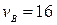 км/год.. Через який час відстань між ними буде найменшою, якщо
км/год.. Через який час відстань між ними буде найменшою, якщо 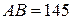 км?
км?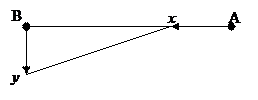
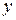 – це відстані пароплава та яхти від точки
– це відстані пароплава та яхти від точки 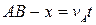 від початкового положення, а яхта пройшла шлях
від початкового положення, а яхта пройшла шлях 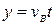 .
. ,
,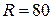 см вписати прямий круговий конус найбільшого об’єму.
см вписати прямий круговий конус найбільшого об’єму. Об’єм конуса дорівнює
Об’єм конуса дорівнює 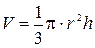 .
.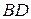 – висота (
– висота ( 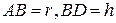 ). Зробимо допоміжні побудови і домалюємо кут
). Зробимо допоміжні побудови і домалюємо кут 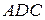 до трикутника. Бачимо, що цей трикутник прямокутний, а відрізок
до трикутника. Бачимо, що цей трикутник прямокутний, а відрізок 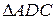 на два подібні прямокутні трикутники
на два подібні прямокутні трикутники 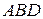 і
і 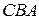 . Отже можемо записати
. Отже можемо записати 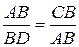 , звідки
, звідки 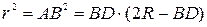 . Знаходимо об’єм
. Знаходимо об’єм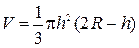 ,
,