Послідовність чисел або функцій, в якій кожен наступний член виражається через попередній, називається рекурентною, а формули, що встановлюють цей зв’язок, – рекурентними співвідношеннями. У вираженні наступного значення деякої величини через її попередні значення і полягає суть методу рекурентних співвідношень.
Якщо послідовність чисел або функцій скінченна, то для знаходження значень функції (наприклад, суми, добутку або 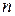 -го члену) використовується арифметичний цикл, тобто цикл, в якому заздалегідь відоме число повторень. Складність при розв’язанні таких задач полягає у знаходженні самої рекурентної формули.
-го члену) використовується арифметичний цикл, тобто цикл, в якому заздалегідь відоме число повторень. Складність при розв’язанні таких задач полягає у знаходженні самої рекурентної формули.
Виведемо рекурентне співвідношення для знаходження членів послідовності:
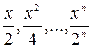
Будь-яких член послідовності можна виразити як попередній помножений на 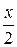 , тобто
, тобто 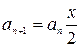 .
.
Візьмемо іншу послідовність:
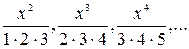
Вираз, що пов’язує наступний член із попереднім, вже не такий очевидний. Щоб знайти цей вираз, спочатку запишемо загальну формулу для будь-якого члену даної послідовності:
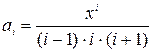 .
.
Тоді 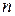 -ий член послідовності прийме вигляд:
-ий член послідовності прийме вигляд: 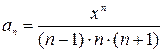 , а
, а 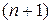 -ий –
-ий – 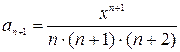 . Розділимо
. Розділимо 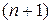 -ий член на
-ий член на 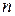 -ий
-ий
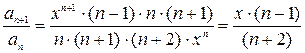 .
.
В результаті отримаємо знаменник послідовності, тобто той множник, який пов’язує наступний член послідовності із попереднім.
Отже, рекурентна формула має вигляд: 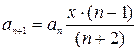 .
.
Перевіримо, чи дійсно за цією формулою можна отримати члени послідовності, що йдуть підряд.
При 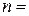 1
1 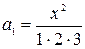 ;
;
При 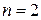
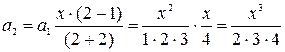 ;
;
При 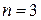
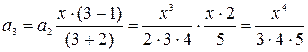 і т.д..
і т.д..
Отримана формула дійсно формує члени послідовності.
Приклад. Бактерії.
Для виробництва вакцини на заводі планується вирощувати культуру бактерій. Відомо, що якщо маса бактерій – 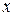 г, то через добу вона збільшується на
г, то через добу вона збільшується на 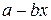 , де коефіцієнти
, де коефіцієнти 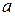 і
і 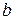 залежать від виду бактерій. Завод щоденно буде забирати для потреб виробництва
залежать від виду бактерій. Завод щоденно буде забирати для потреб виробництва 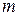 г бактерій. Як буде змінюватися маса бактерій впродовж 90 днів?
г бактерій. Як буде змінюватися маса бактерій впродовж 90 днів?
Інформаційна модель:
| Об’єкт
| Параметри
|
| Назва
| Значення
|
| Бактерії
| Початкова маса 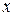 , г , г
|
|
| Щоденний приріст культури бактерій
| 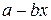 , де , де 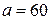 , , 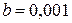
|
Завод забирає на потреби виробництва 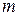 , г , г
|
|
Розробка комп’ютерної моделі:
Нам необхідно розрахувати, як буде змінюватися маса культури бактерій в залежності від часу (який вимірюється в днях). За умовою задачі кожного дня маса бактерій збільшується на 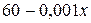 , а завод забирає 50 г. Отже ми можемо розрахувати масу бактерій певного дня, використовуючи значення маси попереднього дня, тобто за допомогою рекурентного співвідношення:
, а завод забирає 50 г. Отже ми можемо розрахувати масу бактерій певного дня, використовуючи значення маси попереднього дня, тобто за допомогою рекурентного співвідношення:
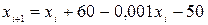 .
.
Тут 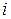 приймає значення від 1 до 90.
приймає значення від 1 до 90.
I спосіб розв’язання:
Будемо будувати комп’ютерну модель у середовищі електронних таблиці Excel. Для цього виконуємо наступні дії:
– вводимо початкові дані;
– вводимо формули для розрахунків за правилами, прийнятими в середовищі електронних таблиць;
– отримуємо масив даних, тобто таблицю, яка відображає залежність маси культури бактерій від часу;
– за отриманими результатами будуємо графік.
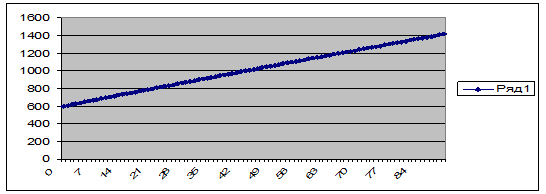
II спосіб розв’язання:
На відміну від електронних таблиць, в Pascal ми не будемо виводити значення маси культури бактерій кожного дня, а виведемо результат, розрахований для певного значення 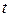 . Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми, написаної на мові Pascal:
. Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми, написаної на мові Pascal:
program z1;
var x,m,a,b:real;
i,t:integer;
begin
Writeln('Vvedite t');
readln(t);
a:=60;
b:=0.001;
m:=50;
x:=600;
i:=0;
while i<=t do
begin
x:=x+(a-b*x)-m;
i:=i+1;
end;
writeln('x=',x);
end.
{час 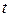 вводиться з клавіатури}
вводиться з клавіатури}
{вводимо константи та початкове значення 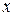 }
}
{розраховуємо
та виводимо значення маси культури бактерій, що відповідає певному значенню 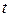 }
}
Завдання для самостійного виконання
1) Падіння з драбиною. Електрик Петров приставив до стіни драбину довжиною 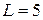 м, що має 10 сходинок, і, піднявшись до гори, зупинився на одній із сходинок. В цей час кінці драбини почали зісковзувати із постійною швидкістю уподовж стіни і підлоги. Провести дослідження, по якій траєкторії буде падати вниз електрик Петров в залежності від того, на якій він сходинці.
м, що має 10 сходинок, і, піднявшись до гори, зупинився на одній із сходинок. В цей час кінці драбини почали зісковзувати із постійною швидкістю уподовж стіни і підлоги. Провести дослідження, по якій траєкторії буде падати вниз електрик Петров в залежності від того, на якій він сходинці.
Формалізація задачі:
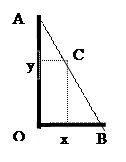 Для того щоб знайти траєкторію падіння Петрова ми маємо простежити траєкторію руху сходинки, на якій стоїть електрик. На малюнку, схематично зображено драбину, яка приставлена до стіни. Початок координат візьмемо в точці О.
Для того щоб знайти траєкторію падіння Петрова ми маємо простежити траєкторію руху сходинки, на якій стоїть електрик. На малюнку, схематично зображено драбину, яка приставлена до стіни. Початок координат візьмемо в точці О. 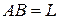 , CB дорівнює добутку номера сходинки, на якій стоїть електрик, на відстань між сходинками
, CB дорівнює добутку номера сходинки, на якій стоїть електрик, на відстань між сходинками 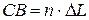 . З подібності трикутників АОВ, AyC і CxB, та за теоремою Піфагора знаходимо функції, за якими змінюються x і y:
. З подібності трикутників АОВ, AyC і CxB, та за теоремою Піфагора знаходимо функції, за якими змінюються x і y:
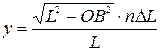 ,
, 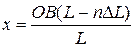 .
.
OB змінюється від 0 до L. Крок змінення ОВ дорівнює 0,2 м.
2) Змінення популяції оленів. Початкова чисельність популяції оленів складає 2000 особин. Оленями харчується хижак – вовк. Частина популяції оленів, яка вижила до кінця року, збільшує свою чисельність на 40%. Початкова чисельність популяції вовків складає 15 особин, один вовк з’їдає 30 оленів за рік. Річний приріст популяції вовків складає 10%. Смертність оленів з інших причин дорівнює нулю. Смертність вовків дорівнює нулю. Розрахувати, як буде змінюватися чисельність оленів впродовж 10 років.
Формалізація задачі:
Із умови задачі відомо, що на чисельність вовків впливає тільки щорічний приріст, тоді цю чисельність можна вирахувати за наступною формулою
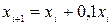 .
.
Чисельність оленів змінюється за двома факторами: річний приріст та смертність, пов’язана із нападами вовків. Тому у формулі має бути відповідний доданок. Співвідношення для розрахунку чисельності оленів матиме вигляд:
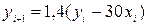 .
.
При створені комп’ютерної моделі врахуйте той факт, що кількість особин популяції має бути цілим числом. Використайте відповідну функцію.
3) Влучення в ціль. В процесі тренування тенісистів використовуються автомати з кидання м’ячика у певне місце площадки. Швидкість м’ячика дорівнює 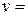 30 м/с, необхідно знайти кут кидання для того, щоб влучити у мішень висотою 1 м на відстані
30 м/с, необхідно знайти кут кидання для того, щоб влучити у мішень висотою 1 м на відстані 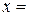 15 м. Кут α змінюється від 0 до π/2. Крок змінення кута Δα = 5 градусів.
15 м. Кут α змінюється від 0 до π/2. Крок змінення кута Δα = 5 градусів.
Формалізація задачі:
Візьмемо за початок координат автомат з кидання м’ячів. Вісь x направимо горизонтально, y – вертикально. Тоді рух м’яча відносно осей буде описуватися наступними функціями: 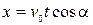 ,
, 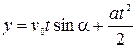 . Тут x дорівнює відстані від автомата до мішені (15 м), щоб дізнатися чи влучив м’яч у мішень ми маємо знайти значення координати y на відстані x. Для цього з першого рівняння виражаємо t та підставляємо у друге:
. Тут x дорівнює відстані від автомата до мішені (15 м), щоб дізнатися чи влучив м’яч у мішень ми маємо знайти значення координати y на відстані x. Для цього з першого рівняння виражаємо t та підставляємо у друге:
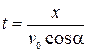 ,
,
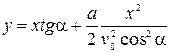 .
.
При розв’язанні цієї задачі на мові програмування необхідно використовувати оператор розгалуження. Правильними будуть ті значення кута, при яких 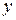 належить проміжку від 0 до 1.
належить проміжку від 0 до 1.
4) Співіснування двох видів. Чисельність особин популяції білок – 10, чисельність особин популяції бурундуків дорівнює 20. Чисельність кожної популяції залежить тільки від співіснування особин цієї популяції між собою та присутності іншої популяції (представники якої вживають ту ж саму їжу). Коефіцієнт впливу родичів в обох популяціях дорівнює 0,01, а коефіцієнт впливу суперників – 0,005. Приріст – 100 %. Розрахувати змінення чисельностей обох популяцій впродовж 5 років.
Формалізація задачі:
Позначимо кількість особин першої популяції К1, а другої популяції – К2. Для розрахунку зміни чисельностей популяцій запишемо наступні рекурентні співвідношення:
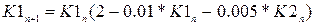
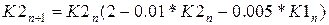
Зверніть увагу на те, що чисельність особин має бути цілим числом.
5) Дачник та собака. Від залізничної станції у напрямку до дачі, відстань до якої 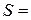 10 км, рухається пішохід зі швидкістю
10 км, рухається пішохід зі швидкістю 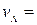 6 км/год. Одночасно з ним у тому ж напрямку біжить собака зі швидкістю
6 км/год. Одночасно з ним у тому ж напрямку біжить собака зі швидкістю 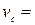 10 км/год. Оскільки собака біжить швидше, то добігши до будинку вона розвертається і біжить до людини, в від неї знову до будинку і так далі. Дослідити процес руху людини і собаки. Встановити зв’язок між відстанями, що пройшли людина і собака. Яку відстань пройшов собака?
10 км/год. Оскільки собака біжить швидше, то добігши до будинку вона розвертається і біжить до людини, в від неї знову до будинку і так далі. Дослідити процес руху людини і собаки. Встановити зв’язок між відстанями, що пройшли людина і собака. Яку відстань пройшов собака?
Формалізація задачі:
Перший раз, від людини до дачі, собака пробіг відстань, яка дорівнює відстані від залізничної станції до дачі 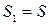 . На шлях він витратив час:
. На шлях він витратив час: 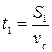 , а людина при цьому пройшла:
, а людина при цьому пройшла: 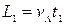 . Відстань, яка була між людиною і собакою, коли вони почали рухатися назустріч одне одному, дорівнює
. Відстань, яка була між людиною і собакою, коли вони почали рухатися назустріч одне одному, дорівнює 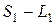 . Вона також може бути представлена як сума відстаней, які пройшли кожен з учасників до зустрічі
. Вона також може бути представлена як сума відстаней, які пройшли кожен з учасників до зустрічі 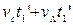 , тут
, тут 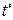 – це час, який собака витратив на шлях, повертаючись від дачі до людини. Прирівнюємо ці вирази:
– це час, який собака витратив на шлях, повертаючись від дачі до людини. Прирівнюємо ці вирази: 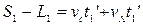 звідси видно, що на зворотній шлях собаці знадобилося часу:
звідси видно, що на зворотній шлях собаці знадобилося часу: 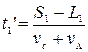 . За цей час людина і собака пройшли шляхи:
. За цей час людина і собака пройшли шляхи: 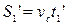 ,
, 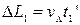 і т.д.. Можемо записати загальні формули:
і т.д.. Можемо записати загальні формули:
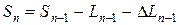 ,
, 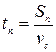 ,
, 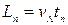
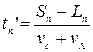 ,
, 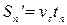 ,
, 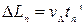
Відповіддю буде сума всіх відрізків шляху, що пройшов собака.
Розв’яжіть цю задачу аналітично, тобто за формулою
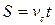 ,
,
де 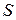 – шлях, що пройшов собака, загальний час руху можемо знайти поділивши відстань між залізничною станцією та дачею на швидкість людини. Порівняйте результати двох розв’язків та визначте похибку розрахунків, проведених за допомогою Excel.
– шлях, що пройшов собака, загальний час руху можемо знайти поділивши відстань між залізничною станцією та дачею на швидкість людини. Порівняйте результати двох розв’язків та визначте похибку розрахунків, проведених за допомогою Excel.
6) Моделювання біоритмів. Розрахувати фізичні, емоційні та інтелектуальні біоритми людини. Відомо, що період змінення фізичного стану людини складає 23 дні, емоційного стану – 28 днів, інтелектуального – 33 дні. Стан людини залежить від дати народження. Зробити прогноз на 30 днів та побудувати графік залежності біоритмів від дати.
Формалізація задачі:
Позначимо період фізичного циклу p1, емоційного циклу – p2, інтелектуального циклу – p3, дуту народження - dr та дату відліку – d0. Нехай дата народження буде 07.08.1990, а дата відліку – 01.06.2010.
Значення фізичного біоритму розраховуються за формулою:
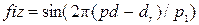 ,
,
де pd – це відповідний день. Значення емоційного біоритму змінюється за законом:
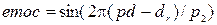 .
.
Значення інтелектуального біоритму:
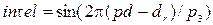 .
.
7) Моделювання процесу народжуваності та смертності. Розглянути процес існування системи, чисельність особин популяції якої залежить тільки від природної народжуваності та смертності. Коефіцієнт народжуваності за рік дорівнює 0,5, а коефіцієнт смертності за рік дорівнює 0,2. Початкова чисельність особин популяції дорівнює 100. Розрахувати, як буде змінюватися чисельність популяції впродовж 20 років та побудувати графік залежності чисельності особин від часу.
Формалізація задачі:
Позначимо коефіцієнт народжуваності Kr, коефіцієнт смертності – Ks, чисельність особин – K. З урахуванням факторів змінення чисельності популяції запишемо наступні рекурентні співвідношення для розрахунку K:
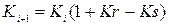 .
.
Перевірте: якщо 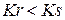 , то популяція не життєздатна. Побудуйте графік. Зверніть увагу на те, що чисельність особин має бути цілим числом.
, то популяція не життєздатна. Побудуйте графік. Зверніть увагу на те, що чисельність особин має бути цілим числом.
8) Розрахунок кількості рулонів шпалер для оклеювання приміщення. Розрахувати необхідну кількість рулонів шпалер для оклеювання приміщення висотою 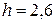 м, довжиною
м, довжиною 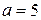 м та шириною
м та шириною 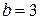 м. При цьому необхідно врахувати , що 15% площі стін кімнати займають вікна і двері, а при розкрої 10% площі рулону йде на обрізки.
м. При цьому необхідно врахувати , що 15% площі стін кімнати займають вікна і двері, а при розкрої 10% площі рулону йде на обрізки.
Формалізація задачі:
Для розрахунку візьмемо 4 зразки шпалер із наступними значеннями довжини 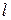 та ширини
та ширини 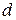 . Зразок1:
. Зразок1: 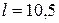 м,
м, 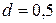 м; зразок2:
м; зразок2: 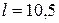 м,
м,  м; зразок3:
м; зразок3: 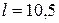 м,
м, 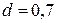 м; зразок4:
м; зразок4: 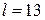 м,
м, 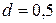 м. Площа стін з урахуванням вікон та дверей дорівнює
м. Площа стін з урахуванням вікон та дверей дорівнює 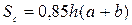 . Площу рулону шпалер з урахуванням обрізків можна знайти за формулою:
. Площу рулону шпалер з урахуванням обрізків можна знайти за формулою: 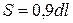 . Кількість рулонів дорівнюватиме відношенню площі стін до площі шпалер в одному рулоні, тобто
. Кількість рулонів дорівнюватиме відношенню площі стін до площі шпалер в одному рулоні, тобто
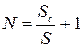 ,
,
тут одиниця це запасний рулон. При побудові комп’ютерної моделі врахуйте, що кількість рулонів шпалер має бути цілим числом.
При побудові комп’ютерної моделі на мові програмування виведіть масив, який відображав би залежність необхідної кількості рулонів шпалер від номеру зразка. Для цього необхідно скористатися масивом.
9) Врожайність. В деякому році (назвемо його умовно першим) на ділянці в 100 гектарів середня врожайність ячменю склала 20 центнерів з гектара. Після цього кожен рік площа ділянки збільшувалася на 5%, а середня врожайність – на 2%. Визначити, який врожай буде зібрано за перші шість років.
Формалізація задачі:
Для того щоб визначити, який врожай було зібрано, необхідно розрахувати площу ділянки та середню врожайність кожного року. Це можна зробити за наступними формулами: 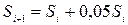 ;
; 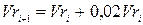 . Врожай кожного року дорівнюватиме добутку
. Врожай кожного року дорівнюватиме добутку
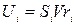 .
.
10) Рух планет. Визначити швидкості руху планет по орбіті. Відстані від планет до Сонця 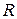 та періоди обороту планет навколо Сонця
та періоди обороту планет навколо Сонця 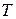 наведені в таблиці:
наведені в таблиці:
| Планети
| Меркурій
| Венера
| Земля
| Марс
| Юпітер
| Сатурн
| Уран
| Нептун
| Плутон
|
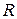 , а.о. , а.о.
| 0,39
| 0,72
| 1,00
| 1,52
| 5,20
| 9,54
| 19,18
| 30,06
| 39,40
|
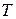 , рік , рік
| 0,24
| 0,62
| 1,00
| 1,88
| 11,86
| 29,46
| 84,02
| 164,79
| 247,70
|
Формалізація задачі:
Припустимо, що планети рухаються навколо Сонця по колах із постійною швидкістю. При такому припущенні швидкість можна знайти як відношення шляху до часу:

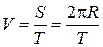 ,
,
де 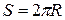 – довжина орбіти відповідної планети,
– довжина орбіти відповідної планети, 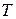 – період обертання планети навколо Сонця (час за який планета робить один оберт). Розрахуйте швидкість руху планет по орбіті в км/год та побудуйте графік у вигляді гістограми для швидкостей. (1 астрономічна одиниця = 150 млн. км).
– період обертання планети навколо Сонця (час за який планета робить один оберт). Розрахуйте швидкість руху планет по орбіті в км/год та побудуйте графік у вигляді гістограми для швидкостей. (1 астрономічна одиниця = 150 млн. км).
При побудові комп’ютерної модель на мові програмування виведіть таблицю, яка б відображала назви планет та їх швидкості руху по орбіті.
11) Голуби. Визначте, як буде змінюватися густина популяції голубів протягом 5 років, якщо попередні спостереження дозволили встановити, що її густина складає 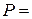 130 особин/га. За період розмноження (у голуба раз на рік) із однієї кладки яєць у середньому виживає 1,3 дитинчат. Смертність голубів складає 27% за рік. При збільшенні густини популяції до 300 особин/га та більше смертність збільшується до 50%.
130 особин/га. За період розмноження (у голуба раз на рік) із однієї кладки яєць у середньому виживає 1,3 дитинчат. Смертність голубів складає 27% за рік. При збільшенні густини популяції до 300 особин/га та більше смертність збільшується до 50%.
Формалізація задачі:
За умовою задачі густина популяції залежить від смертності та народжуваності. Щоб знайти народжуваність, необхідно знайти кількість самок та помножити її на плодовитість. Припустимо, що в популяції рівна кількість самок та самців. Тоді приріст популяції дорівнюватиме 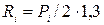 , а смертність:
, а смертність: 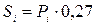 або
або 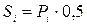 , якщо густина популяції складає більше 300 особин/га. Густина популяції кожного наступного року буде розраховуватися за формулою:
, якщо густина популяції складає більше 300 особин/га. Густина популяції кожного наступного року буде розраховуватися за формулою:
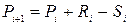 .
.
Побудуйте в одній системі координат графіки змінення густини, народжуваності та смертності популяції голубів за 5 років. Зверніть увагу на те, що чисельність особин має бути цілим числом.
12) Кролики. Кожного місяця кожна пара кроликів приносить приплід – нову пару: самця та самку, які в свою чергу починають давати потомство через два місяці. Треба визначити, якої чисельності досягне популяція кроликів через рік. Смертність не враховується. За початкову кількість 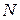 взяти пару новонароджених кроленят (самця та самку).
взяти пару новонароджених кроленят (самця та самку).
Формалізація задачі:
За умовою задачі на приріст кроликів впливає тільки народжуваність, до того ж кожна пара починає давати потомство тільки через 2 місяці після народження. Звідси бачимо, що у другий місяць кількість кроликів не зміниться. Якщо розглядати популяцію не як кількість особин, а як кількість пар кроликів, то змінення їх кількості буде відповідати ряду Фібоначчі. Кожен наступний член якого можна знайти як суму попередніх двох:
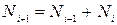 .
.
Тут 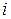 змінюється від 3 до 10. Побудуйте графік залежності змінення популяції кроликів від часу.
змінюється від 3 до 10. Побудуйте графік залежності змінення популяції кроликів від часу.


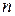 -го члену) використовується арифметичний цикл, тобто цикл, в якому заздалегідь відоме число повторень. Складність при розв’язанні таких задач полягає у знаходженні самої рекурентної формули.
-го члену) використовується арифметичний цикл, тобто цикл, в якому заздалегідь відоме число повторень. Складність при розв’язанні таких задач полягає у знаходженні самої рекурентної формули.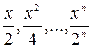
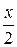 , тобто
, тобто 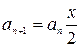 .
.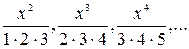
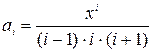 .
.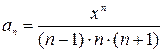 , а
, а 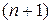 -ий –
-ий – 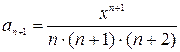 . Розділимо
. Розділимо 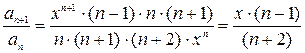 .
.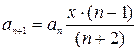 .
.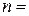 1
1 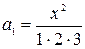 ;
;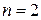
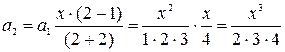 ;
;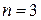
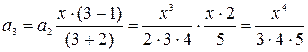 і т.д..
і т.д..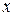 г, то через добу вона збільшується на
г, то через добу вона збільшується на 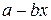 , де коефіцієнти
, де коефіцієнти 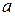 і
і 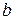 залежать від виду бактерій. Завод щоденно буде забирати для потреб виробництва
залежать від виду бактерій. Завод щоденно буде забирати для потреб виробництва 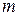 г бактерій. Як буде змінюватися маса бактерій впродовж 90 днів?
г бактерій. Як буде змінюватися маса бактерій впродовж 90 днів?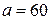 ,
, 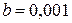
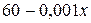 , а завод забирає 50 г. Отже ми можемо розрахувати масу бактерій певного дня, використовуючи значення маси попереднього дня, тобто за допомогою рекурентного співвідношення:
, а завод забирає 50 г. Отже ми можемо розрахувати масу бактерій певного дня, використовуючи значення маси попереднього дня, тобто за допомогою рекурентного співвідношення: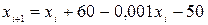 .
.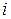 приймає значення від 1 до 90.
приймає значення від 1 до 90.
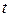 . Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми, написаної на мові Pascal:
. Це значення задається на початку роботи програми з клавіатури. Нижче представлено текст програми, написаної на мові Pascal: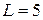 м, що має 10 сходинок, і, піднявшись до гори, зупинився на одній із сходинок. В цей час кінці драбини почали зісковзувати із постійною швидкістю уподовж стіни і підлоги. Провести дослідження, по якій траєкторії буде падати вниз електрик Петров в залежності від того, на якій він сходинці.
м, що має 10 сходинок, і, піднявшись до гори, зупинився на одній із сходинок. В цей час кінці драбини почали зісковзувати із постійною швидкістю уподовж стіни і підлоги. Провести дослідження, по якій траєкторії буде падати вниз електрик Петров в залежності від того, на якій він сходинці. Для того щоб знайти траєкторію падіння Петрова ми маємо простежити траєкторію руху сходинки, на якій стоїть електрик. На малюнку, схематично зображено драбину, яка приставлена до стіни. Початок координат візьмемо в точці О.
Для того щоб знайти траєкторію падіння Петрова ми маємо простежити траєкторію руху сходинки, на якій стоїть електрик. На малюнку, схематично зображено драбину, яка приставлена до стіни. Початок координат візьмемо в точці О. 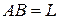 , CB дорівнює добутку номера сходинки, на якій стоїть електрик, на відстань між сходинками
, CB дорівнює добутку номера сходинки, на якій стоїть електрик, на відстань між сходинками 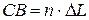 . З подібності трикутників АОВ, AyC і CxB, та за теоремою Піфагора знаходимо функції, за якими змінюються x і y:
. З подібності трикутників АОВ, AyC і CxB, та за теоремою Піфагора знаходимо функції, за якими змінюються x і y: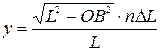 ,
, 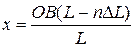 .
.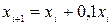 .
.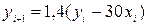 .
.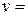 30 м/с, необхідно знайти кут кидання для того, щоб влучити у мішень висотою 1 м на відстані
30 м/с, необхідно знайти кут кидання для того, щоб влучити у мішень висотою 1 м на відстані 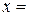 15 м. Кут α змінюється від 0 до π/2. Крок змінення кута Δα = 5 градусів.
15 м. Кут α змінюється від 0 до π/2. Крок змінення кута Δα = 5 градусів.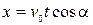 ,
, 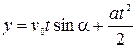 . Тут x дорівнює відстані від автомата до мішені (15 м), щоб дізнатися чи влучив м’яч у мішень ми маємо знайти значення координати y на відстані x. Для цього з першого рівняння виражаємо t та підставляємо у друге:
. Тут x дорівнює відстані від автомата до мішені (15 м), щоб дізнатися чи влучив м’яч у мішень ми маємо знайти значення координати y на відстані x. Для цього з першого рівняння виражаємо t та підставляємо у друге: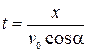 ,
,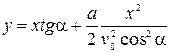 .
.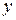 належить проміжку від 0 до 1.
належить проміжку від 0 до 1.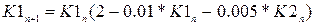
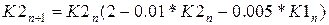
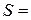 10 км, рухається пішохід зі швидкістю
10 км, рухається пішохід зі швидкістю 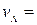 6 км/год. Одночасно з ним у тому ж напрямку біжить собака зі швидкістю
6 км/год. Одночасно з ним у тому ж напрямку біжить собака зі швидкістю 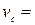 10 км/год. Оскільки собака біжить швидше, то добігши до будинку вона розвертається і біжить до людини, в від неї знову до будинку і так далі. Дослідити процес руху людини і собаки. Встановити зв’язок між відстанями, що пройшли людина і собака. Яку відстань пройшов собака?
10 км/год. Оскільки собака біжить швидше, то добігши до будинку вона розвертається і біжить до людини, в від неї знову до будинку і так далі. Дослідити процес руху людини і собаки. Встановити зв’язок між відстанями, що пройшли людина і собака. Яку відстань пройшов собака?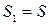 . На шлях він витратив час:
. На шлях він витратив час: 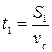 , а людина при цьому пройшла:
, а людина при цьому пройшла: 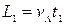 . Відстань, яка була між людиною і собакою, коли вони почали рухатися назустріч одне одному, дорівнює
. Відстань, яка була між людиною і собакою, коли вони почали рухатися назустріч одне одному, дорівнює 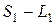 . Вона також може бути представлена як сума відстаней, які пройшли кожен з учасників до зустрічі
. Вона також може бути представлена як сума відстаней, які пройшли кожен з учасників до зустрічі 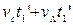 , тут
, тут 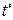 – це час, який собака витратив на шлях, повертаючись від дачі до людини. Прирівнюємо ці вирази:
– це час, який собака витратив на шлях, повертаючись від дачі до людини. Прирівнюємо ці вирази: 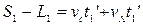 звідси видно, що на зворотній шлях собаці знадобилося часу:
звідси видно, що на зворотній шлях собаці знадобилося часу: 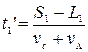 . За цей час людина і собака пройшли шляхи:
. За цей час людина і собака пройшли шляхи: 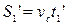 ,
, 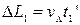 і т.д.. Можемо записати загальні формули:
і т.д.. Можемо записати загальні формули: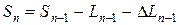 ,
, 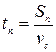 ,
, 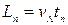
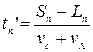 ,
, 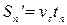 ,
, 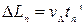
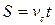 ,
,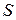 – шлях, що пройшов собака, загальний час руху можемо знайти поділивши відстань між залізничною станцією та дачею на швидкість людини. Порівняйте результати двох розв’язків та визначте похибку розрахунків, проведених за допомогою Excel.
– шлях, що пройшов собака, загальний час руху можемо знайти поділивши відстань між залізничною станцією та дачею на швидкість людини. Порівняйте результати двох розв’язків та визначте похибку розрахунків, проведених за допомогою Excel.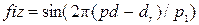 ,
,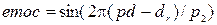 .
.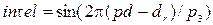 .
.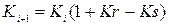 .
.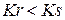 , то популяція не життєздатна. Побудуйте графік. Зверніть увагу на те, що чисельність особин має бути цілим числом.
, то популяція не життєздатна. Побудуйте графік. Зверніть увагу на те, що чисельність особин має бути цілим числом.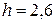 м, довжиною
м, довжиною 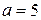 м та шириною
м та шириною 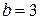 м. При цьому необхідно врахувати , що 15% площі стін кімнати займають вікна і двері, а при розкрої 10% площі рулону йде на обрізки.
м. При цьому необхідно врахувати , що 15% площі стін кімнати займають вікна і двері, а при розкрої 10% площі рулону йде на обрізки.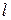 та ширини
та ширини 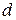 . Зразок1:
. Зразок1: 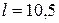 м,
м, 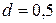 м; зразок2:
м; зразок2:  м; зразок3:
м; зразок3: 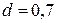 м; зразок4:
м; зразок4: 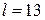 м,
м, 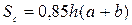 . Площу рулону шпалер з урахуванням обрізків можна знайти за формулою:
. Площу рулону шпалер з урахуванням обрізків можна знайти за формулою: 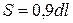 . Кількість рулонів дорівнюватиме відношенню площі стін до площі шпалер в одному рулоні, тобто
. Кількість рулонів дорівнюватиме відношенню площі стін до площі шпалер в одному рулоні, тобто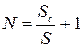 ,
,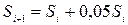 ;
; 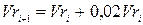 . Врожай кожного року дорівнюватиме добутку
. Врожай кожного року дорівнюватиме добутку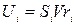 .
.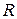 та періоди обороту планет навколо Сонця
та періоди обороту планет навколо Сонця 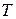 наведені в таблиці:
наведені в таблиці:
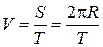 ,
,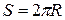 – довжина орбіти відповідної планети,
– довжина орбіти відповідної планети, 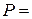 130 особин/га. За період розмноження (у голуба раз на рік) із однієї кладки яєць у середньому виживає 1,3 дитинчат. Смертність голубів складає 27% за рік. При збільшенні густини популяції до 300 особин/га та більше смертність збільшується до 50%.
130 особин/га. За період розмноження (у голуба раз на рік) із однієї кладки яєць у середньому виживає 1,3 дитинчат. Смертність голубів складає 27% за рік. При збільшенні густини популяції до 300 особин/га та більше смертність збільшується до 50%.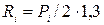 , а смертність:
, а смертність: 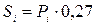 або
або 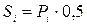 , якщо густина популяції складає більше 300 особин/га. Густина популяції кожного наступного року буде розраховуватися за формулою:
, якщо густина популяції складає більше 300 особин/га. Густина популяції кожного наступного року буде розраховуватися за формулою: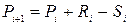 .
.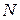 взяти пару новонароджених кроленят (самця та самку).
взяти пару новонароджених кроленят (самця та самку).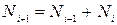 .
.