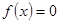 , (1)
, (1)
складається з двох етапів: відокремлення коренів, тобто встановлення проміжків 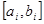 ,
, 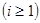 , в кожному з яких міститься тільки один корінь; уточнення коренів, тобто їх обчислення з наперед заданою точністю
, в кожному з яких міститься тільки один корінь; уточнення коренів, тобто їх обчислення з наперед заданою точністю 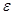 . Для відокремлення коренів використовуються аналітичні або графічні методи. Для уточнення коренів використовуються ітераційні методи. Розглянемо деякі методи уточнення коренів.
. Для відокремлення коренів використовуються аналітичні або графічні методи. Для уточнення коренів використовуються ітераційні методи. Розглянемо деякі методи уточнення коренів.
1. Метод поділу проміжку навпіл. Якщо функція 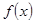 неперервна і набуває на кінцях проміжку
неперервна і набуває на кінцях проміжку 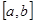 значень різних знаків, тобто
значень різних знаків, тобто 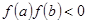 , то корінь рівняння (1)
, то корінь рівняння (1) 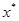 можна обчислити з наперед заданою точністю
можна обчислити з наперед заданою точністю 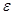 . Побудуємо обчислювальний процес. Обчислимо середину проміжку
. Побудуємо обчислювальний процес. Обчислимо середину проміжку 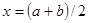 . Оскільки
. Оскільки 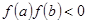 , то буде:
, то буде: 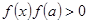 , або
, або 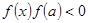 , або
, або 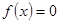 . Якщо
. Якщо 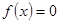 , то знайдено точне значення кореня
, то знайдено точне значення кореня 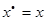 і процес завершується. При
і процес завершується. При 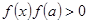 корінь міститься на проміжку
корінь міститься на проміжку 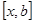 . Покладемо
. Покладемо 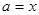 . При
. При 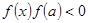 корінь міститься на проміжку
корінь міститься на проміжку 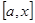 .і Покладемо
.і Покладемо 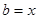 . Якщо довжина проміжку
. Якщо довжина проміжку 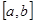 більша за
більша за 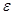 , то знову обчислюється середина проміжку і т. д. Якщо довжина проміжку
, то знову обчислюється середина проміжку і т. д. Якщо довжина проміжку 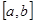 менша за
менша за 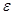 , то процес обчислень завершується, а
, то процес обчислень завершується, а 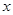 вважається наближенням кореня
вважається наближенням кореня 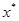 з точністю
з точністю 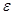 .
.
2. Метод ітерацій. Нехай на проміжку 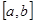 рівняння (1), де
рівняння (1), де 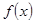 неперервна на
неперервна на 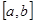 функція, має єдиний корінь
функція, має єдиний корінь 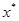 . Замінимо рівняння (1) еквівалентним йому рівнянням
. Замінимо рівняння (1) еквівалентним йому рівнянням 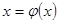 так, щоб
так, щоб 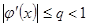 ,
, 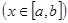 , а всі значення
, а всі значення 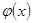 належали проміжку
належали проміжку 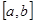 при
при 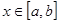 .
.
Починаючи з деякого початкового наближення 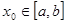 , знаходимо послідовні наближення
, знаходимо послідовні наближення 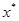 за формулою
за формулою
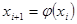 ,
, 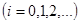 . (2)
. (2)
Обчислення завершуються при виконані умови
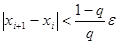 , (3)
, (3)
при цьому 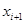 вважається наближеним значенням кореня
вважається наближеним значенням кореня 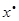 з заданою точністю
з заданою точністю 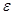 .
.
Рівняння (1) завжди можна подати у вигляді 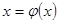 так, щоб справджувалися вище наведені умови, наприклад,
так, щоб справджувалися вище наведені умови, наприклад,
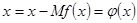 , (4)
, (4)
де 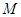 – стала. При
– стала. При 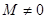 рівняння (4) і (1) еквівалентні. Сталу
рівняння (4) і (1) еквівалентні. Сталу 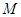 добирають так, щоб в околі кореня
добирають так, щоб в околі кореня 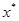 було
було 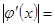
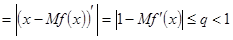 тобто, щоб задовольнялися умови
тобто, щоб задовольнялися умови 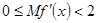 . Отже стала
. Отже стала 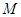 повинна мати той самий знак, що й
повинна мати той самий знак, що й 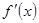 , і задовольняти умову
, і задовольняти умову 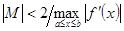 . Процес збігається тим швидше, чим ближче
. Процес збігається тим швидше, чим ближче 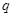 до нуля. Отже,
до нуля. Отже, 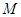 слід добирати так, щоб добуток
слід добирати так, щоб добуток 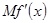 був якомога ближчим до
був якомога ближчим до 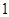 для всіх
для всіх 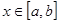 .
.
3. Метод хорд (січних).Якщо функція 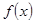 двічі неперервно диференційовна на проміжку
двічі неперервно диференційовна на проміжку 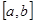 , похідні
, похідні 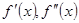 відмінні від нуля і зберігають знак на цьому проміжку, а
відмінні від нуля і зберігають знак на цьому проміжку, а 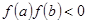 , то за методом хорд наближене значення кореня
, то за методом хорд наближене значення кореня 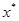 знаходять як абсцису точки перетину хорди, що проходить через точки
знаходять як абсцису точки перетину хорди, що проходить через точки 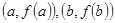 , з віссю
, з віссю 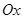 .
.
Послідовні наближення кореня 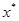 знаходять за формулою
знаходять за формулою
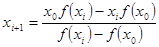 ,
, 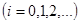 , (5)
, (5)
де 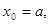 якщо
якщо 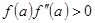 , або
, або 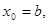 якщо
якщо 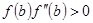 . Обчислення завершуються при виконанні умови
. Обчислення завершуються при виконанні умови
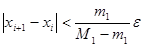 , (6)
, (6)
де 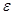 – задана точність,
– задана точність, 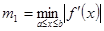 ,
, 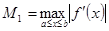 При цьому
При цьому 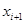 вважається наближеним значенням кореня
вважається наближеним значенням кореня 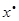 з заданою точністю
з заданою точністю 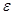 .
.
4. Метод дотичних (Ньютона).Якщо функція 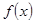 задовольняє ті ж умови, що й у методі хорд, то за методом дотичних наближене значення кореня
задовольняє ті ж умови, що й у методі хорд, то за методом дотичних наближене значення кореня 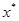 знаходять як абсцису точки перетину дотичної до кривої
знаходять як абсцису точки перетину дотичної до кривої 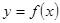 в одній із точок
в одній із точок 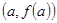 чи
чи 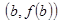 з віссю
з віссю 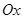 .
.
Послідовні наближення кореня 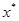 знаходять за формулою
знаходять за формулою
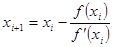 ,
, 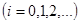 , (7)
, (7)
де 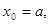 якщо
якщо 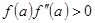 , або
, або 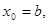 якщо
якщо 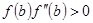 . Обчислення завершуються при виконані умови
. Обчислення завершуються при виконані умови
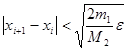 , (8)
, (8)
де 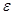 – задана точність,
– задана точність, 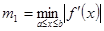 ,
, 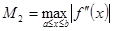 , при цьому
, при цьому 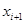 вважається наближеним значенням кореня
вважається наближеним значенням кореня 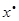 з заданою точністю
з заданою точністю 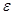 .
.
5. Комбінований метод. Якщо функція 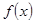 задовольняє ті ж умови, що й у методі хорд, і в методі дотичних, то для уточнення кореня
задовольняє ті ж умови, що й у методі хорд, і в методі дотичних, то для уточнення кореня 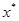 зручно комбінувати метод хорд і метод дотичних. При цьому одержуються оцінки кореня
зручно комбінувати метод хорд і метод дотичних. При цьому одержуються оцінки кореня 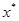 зверху і знизу.
зверху і знизу.
Послідовні наближення кореня 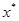 знаходять за формулами
знаходять за формулами
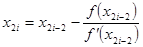 , (9)
, (9)
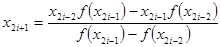 ,
, 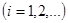 , (10)
, (10)
де 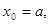
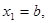 якщо
якщо 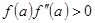 , або
, або 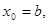
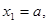 якщо
якщо 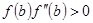 .
.
Обчислення завершуються при виконанні умови
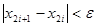 , (11)
, (11)
де 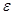 – задана точність, при цьому
– задана точність, при цьому 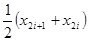 вважається наближеним значенням кореня
вважається наближеним значенням кореня 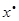 з заданою точністю
з заданою точністю 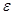 .
.
Завдання:
Розробити програму обчислення таблиці значень інтеграла з заданою точністю 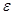 для
для 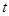 , що змінюється на інтервалі
, що змінюється на інтервалі 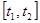 з кроком
з кроком 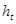 . Для обчислення значення інтеграла використати одну із формул наближеного інтегрування для завдань: 1-4 – прямокутників; 5-9 – трапецій; 10-14 – Сімпсона. У програмі використати підпрограму обчислення інтеграла за вказаною формулою, в яку передати підінтегральну функцію як параметр. Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення
. Для обчислення значення інтеграла використати одну із формул наближеного інтегрування для завдань: 1-4 – прямокутників; 5-9 – трапецій; 10-14 – Сімпсона. У програмі використати підпрограму обчислення інтеграла за вказаною формулою, в яку передати підінтегральну функцію як параметр. Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення 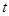 і відповідне йому значення інтеграла.
і відповідне йому значення інтеграла.
1. 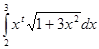 ,
, 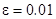 ,
, 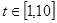 ,
, 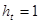 .
.
2. 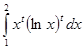 ,
, 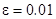 ,
, 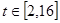 ,
, 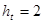 .
.
3. 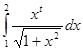 ,
, 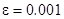 ,
, 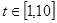 ,
, 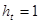 .
.
4. 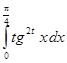 ,
, 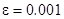 ,
, 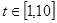 ,
, 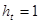 .
.
5. 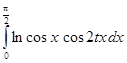 ,
, 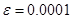 ,
, 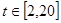 ,
, 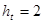 .
.
6. 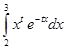 ,
, 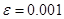 ,
, 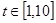 ,
, 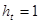 .
.
7. 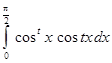 ,
, 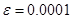 ,
, 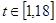 ,
, 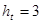 .
.
8. 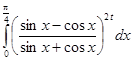 ,
, 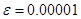 ,
, 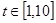 ,
, 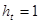 .
.
9. 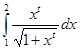 ,
, 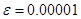 ,
, 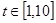 ,
, 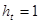 .
.
10. 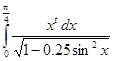 ,
, 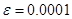 ,
, 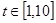 ,
, 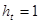 .
.
11. 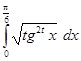 ,
, 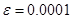 ,
, 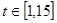 ,
, 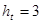 .
.
12. 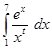 ,
, 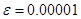 ,
, 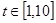 ,
, 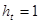 .
.
13. 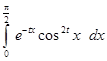 ,
, 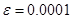 ,
, 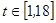 ,
, 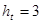 .
.
14. 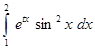 ,
, 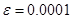 ,
, 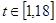 ,
, 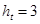 .
.
Розробити програму уточнення коренів рівняння 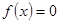 на відрізку
на відрізку 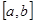 з різною точністю
з різною точністю 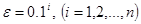 . Для уточнення коренів рівняння використати один із ітераційних методів для завдань: 15-18 – поділу відрізка навпіл; 19-21 – ітерацій; 22-24 – хорд; 25-27 – дотичних; 28-30 – комбінований. У програмі використати підпрограму уточнення коренів рівняння за вказаним методом, в яку передати як параметр функцію обчислення
. Для уточнення коренів рівняння використати один із ітераційних методів для завдань: 15-18 – поділу відрізка навпіл; 19-21 – ітерацій; 22-24 – хорд; 25-27 – дотичних; 28-30 – комбінований. У програмі використати підпрограму уточнення коренів рівняння за вказаним методом, в яку передати як параметр функцію обчислення 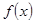 . Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення
. Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення 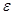 і відповідне йому значення кореня.
і відповідне йому значення кореня.
15. 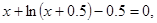
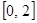 ,
, 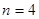 .
.
16. 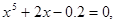
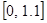 ,
, 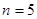 .
.
17. 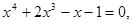
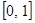 ,
, 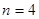 .
.
18. 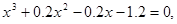
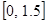 ,
, 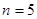 .
.
19. 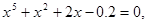
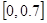
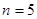 .
.
20. 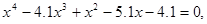
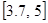 ,
, 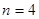 .
.
21. 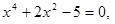
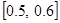 ,
, 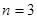 .
.
22. 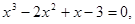
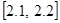 ,
, 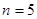 .
.
23. 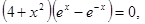
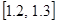 ,
, 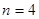 .
.
24. 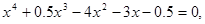
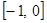 ,
, 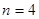 .
.
25. 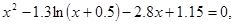
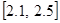 ,
, 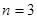 .
.
26. 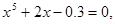
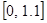 ,
, 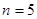 .
.
27. 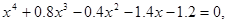
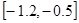 ,
, 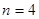 .
.
28. 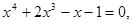
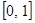 ,
, 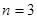 .
.
29. 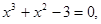
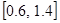 ,
, 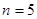 .
.
30. 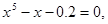
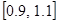 ,
, 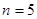 .
.


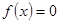 , (1)
, (1)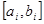 ,
, 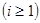 , в кожному з яких міститься тільки один корінь; уточнення коренів, тобто їх обчислення з наперед заданою точністю
, в кожному з яких міститься тільки один корінь; уточнення коренів, тобто їх обчислення з наперед заданою точністю 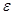 . Для відокремлення коренів використовуються аналітичні або графічні методи. Для уточнення коренів використовуються ітераційні методи. Розглянемо деякі методи уточнення коренів.
. Для відокремлення коренів використовуються аналітичні або графічні методи. Для уточнення коренів використовуються ітераційні методи. Розглянемо деякі методи уточнення коренів.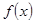 неперервна і набуває на кінцях проміжку
неперервна і набуває на кінцях проміжку 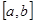 значень різних знаків, тобто
значень різних знаків, тобто 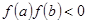 , то корінь рівняння (1)
, то корінь рівняння (1) 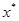 можна обчислити з наперед заданою точністю
можна обчислити з наперед заданою точністю 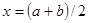 . Оскільки
. Оскільки 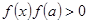 , або
, або 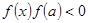 , або
, або 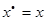 і процес завершується. При
і процес завершується. При 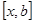 . Покладемо
. Покладемо 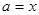 . При
. При 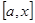 .і Покладемо
.і Покладемо 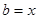 . Якщо довжина проміжку
. Якщо довжина проміжку 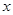 вважається наближенням кореня
вважається наближенням кореня 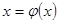 так, щоб
так, щоб 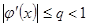 ,
, 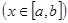 , а всі значення
, а всі значення 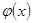 належали проміжку
належали проміжку 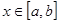 .
.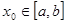 , знаходимо послідовні наближення
, знаходимо послідовні наближення 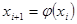 ,
, 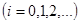 . (2)
. (2)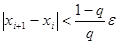 , (3)
, (3)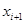 вважається наближеним значенням кореня
вважається наближеним значенням кореня 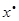 з заданою точністю
з заданою точністю 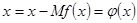 , (4)
, (4)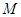 – стала. При
– стала. При 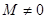 рівняння (4) і (1) еквівалентні. Сталу
рівняння (4) і (1) еквівалентні. Сталу 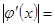
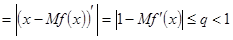 тобто, щоб задовольнялися умови
тобто, щоб задовольнялися умови 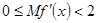 . Отже стала
. Отже стала 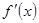 , і задовольняти умову
, і задовольняти умову 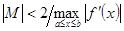 . Процес збігається тим швидше, чим ближче
. Процес збігається тим швидше, чим ближче 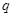 до нуля. Отже,
до нуля. Отже, 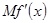 був якомога ближчим до
був якомога ближчим до 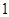 для всіх
для всіх 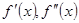 відмінні від нуля і зберігають знак на цьому проміжку, а
відмінні від нуля і зберігають знак на цьому проміжку, а 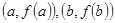 , з віссю
, з віссю 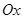 .
.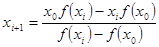 ,
, 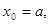 якщо
якщо 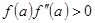 , або
, або 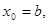 якщо
якщо 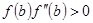 . Обчислення завершуються при виконанні умови
. Обчислення завершуються при виконанні умови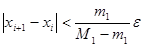 , (6)
, (6)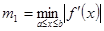 ,
, 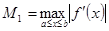 При цьому
При цьому 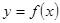 в одній із точок
в одній із точок 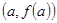 чи
чи 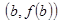 з віссю
з віссю 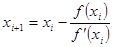 ,
, 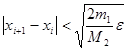 , (8)
, (8)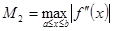 , при цьому
, при цьому 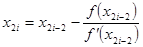 , (9)
, (9)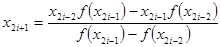 ,
, 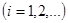 , (10)
, (10)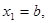 якщо
якщо 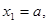 якщо
якщо 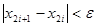 , (11)
, (11)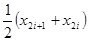 вважається наближеним значенням кореня
вважається наближеним значенням кореня 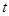 , що змінюється на інтервалі
, що змінюється на інтервалі 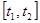 з кроком
з кроком 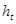 . Для обчислення значення інтеграла використати одну із формул наближеного інтегрування для завдань: 1-4 – прямокутників; 5-9 – трапецій; 10-14 – Сімпсона. У програмі використати підпрограму обчислення інтеграла за вказаною формулою, в яку передати підінтегральну функцію як параметр. Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення
. Для обчислення значення інтеграла використати одну із формул наближеного інтегрування для завдань: 1-4 – прямокутників; 5-9 – трапецій; 10-14 – Сімпсона. У програмі використати підпрограму обчислення інтеграла за вказаною формулою, в яку передати підінтегральну функцію як параметр. Результати обчислень надрукувати у вигляді таблиці, в кожному рядку якої розмістити значення 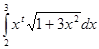 ,
, 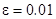 ,
, 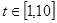 ,
, 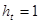 .
.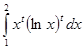 ,
, 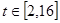 ,
, 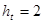 .
.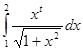 ,
, 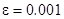 ,
, 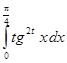 ,
, 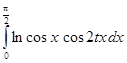 ,
, 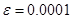 ,
, 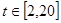 ,
, 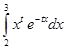 ,
, 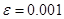 ,
, 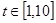 ,
, 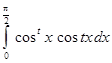 ,
, 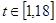 ,
, 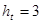 .
.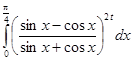 ,
, 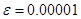 ,
, 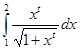 ,
, 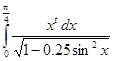 ,
, 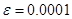 ,
, 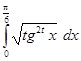 ,
, 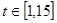 ,
, 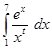 ,
, 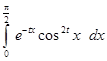 ,
, 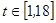 ,
, 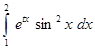 ,
, 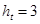 .
.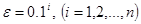 . Для уточнення коренів рівняння використати один із ітераційних методів для завдань: 15-18 – поділу відрізка навпіл; 19-21 – ітерацій; 22-24 – хорд; 25-27 – дотичних; 28-30 – комбінований. У програмі використати підпрограму уточнення коренів рівняння за вказаним методом, в яку передати як параметр функцію обчислення
. Для уточнення коренів рівняння використати один із ітераційних методів для завдань: 15-18 – поділу відрізка навпіл; 19-21 – ітерацій; 22-24 – хорд; 25-27 – дотичних; 28-30 – комбінований. У програмі використати підпрограму уточнення коренів рівняння за вказаним методом, в яку передати як параметр функцію обчислення 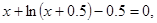
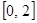 ,
, 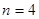 .
.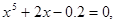
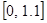 ,
, 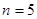 .
.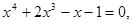
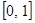 ,
, 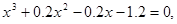
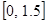 ,
, 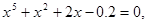
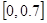
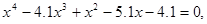
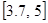 ,
, 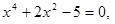
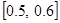 ,
, 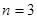 .
.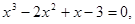
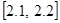 ,
, 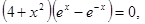
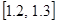 ,
, 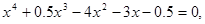
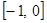 ,
, 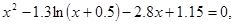
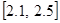 ,
, 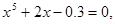
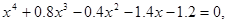
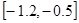 ,
, 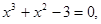
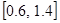 ,
, 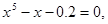
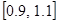 ,
,