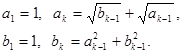Програми, в яких використовуються рекурсивні процедури і функції, відрізняються простотою і наглядністю, але вони вимагають більше пам’яті і виконуються, як правило, повільніше.
Виклик рекурсивної процедури або функції повинен здійснюватися за умови, яка на деякому рівні рекурсії стає хибною і процес завершується, інакше процес зациклюється, що зумовлює переповнення стека.
Рекурсивний виклик може бути прямим і непрямим. При непрямому викликові підпрограма звертається до себе опосередковано як виклик з іншої підпрограми. У цьому випадку використовується директива FORWARD.
Розглянемо приклад прямого рекурсивного виклику.
Приклад.Обчислити значення виразів:
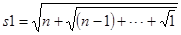 ,
, 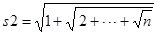 .
.
Для розв’язання задачі командою File|New Application створимо новий проект. Установимо формі заголовок Caption = Рекурсивне обчислення виразів та присвоїмо їй програмне ім’я Name = FROV. Командою File|Save All запишемо програмний модуль під іменем ULAB10_1.pas, а проект – LAB10_1.dpr.
Розробимо форму для введення початкових даних і виведення результату Для цього розмістимо на формі один компонент Edit для введення початкових даних і два для виведення результатів. Присвоїмо цим компонентам програмні імена Edit1, Edit2, Edit3, встановлені за замовчуванням (властивість Name), і очистимо їм значення властивості Text.
Пояснення до цих компонентів зробимо за допомогою компонента Label (властивість Caption).
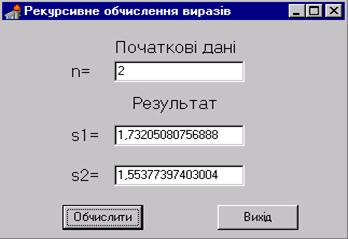
Крім цього, розмістимо на формі дві керуючих кнопки (компонент Button) з написами Обчислити та Вихід (властивість Caption) Рис 10.1.
Рис 10.1. Форма Рекурсивне обчислення виразів
Обробник кнопки Обчислити міститься у програмному модулі ULAB10_1.
Unit ULAB10_1;
. . . . . . . . . . . . . . . . . . . .
{ Обробник кнопки Обчислити }
procedure TFOVR.Button1Click(Sender: TObject);
VAR n, i: integer;
s1,s2: real;
{Рекурсивні функції обчислення коренів}
Function Kor1(n: integer ): real;
begin
if n=1 then result:=1
else result:=sqrt(n+Kor1(n-1));
end;
Function Kor2(i, n: integer ): real;
begin
if i=n then result:=sqrt(n)
else result:=sqrt(i+Kor2(i+1,n));
end;
begin
{Введення початкових даних}
n:=StrToInt(Edit1.Text);
{Обчислення коренів}
s1:=Kor1(n);
s2:=Kor2(1,n);
{Виведення результатів}
Edit2.Text:=FloatToStr(s1);
Edit3.Text:=FloatToStr(s2);
end;
Розглянемо приклад непрямого рекурсивного виклику.
Приклад. Для заданого 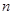 обчислити значення суми
обчислити значення суми
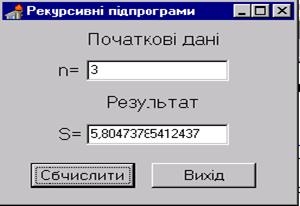
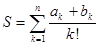 , де
, де 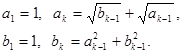
Для розв’язання задачі командою File|New Application створимо новий проект.
Рис. 10.2. Форма Рекурсивні підпрограми
Установимо формі заголовок Caption = Рекурсивні підпрограми Командою File|Save All запишемо програмний модуль під іменем ULAB10_2.pas, а проект – PLAB10_2.dpr.
Аналогічно, як у попередньому прикладі, розробимо форму для введення початкових даних і виведення результату. Обробник кнопки Обчислити міститься у програмному модулі ULAB10_2.
Unit ULAB10_2;
. . . . . . . . . . . . . . . .
{ Обробник кнопки Обчислити }
procedure TFR.Button1Click(Sender: TObject);
VAR n: integer;
s: real;
{Попередній опис функції Ak}
Function Ak(k: integer ): real;
FORWARD;
{Функція обчислення Bk}
Function Bk(k: integer ): real;
begin
if k=1 then result:=1
else result:=sqr(Ak(k-1))+sqr(Bk(k-1));
end;
{Функція обчислення Ak}
Function Ak(k: integer ): real;
begin
if k=1 then result:=1
else result:=sqrt(Ak(k-1))+sqrt(Bk(k-1));
end;
{Функція обчислення факторіала}
Function Fact(k: integer ): longint;
begin
if (k=0) or (k=1) then result:=1
else result:=Fact(k-1)*k;
end;
{Функція обчислення суми}
Function Sum(k: integer ): double;
begin
if k=1 then result:=2
else result:=Sum(k-1)+(Ak(k)+Bk(k))/Fact(k);
end;
begin
{Введення початкових даних}
n:=StrToInt(Edit1.Text);
{Обчислення суми}
s:=Sum(n);
{Виведення результату}
Edit2.Text:=FloatToStr(s);
end;
end.


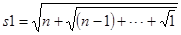 ,
, 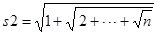 .
.
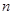 обчислити значення суми
обчислити значення суми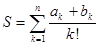 , де
, де