Нехай джерела з густиною струмів 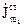 зосередженні в об’ємі
зосередженні в об’ємі  , а джерела з густиною струмів
, а джерела з густиною струмів 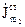 – в об’ємі
– в об’ємі 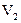 . Області об’ємів
. Області об’ємів  і
і 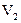 просторово не перетинаються (рис. 4.6).
просторово не перетинаються (рис. 4.6).
Якщо розповсюдити інтегрування в рівнянні (4.61) на весь простір, при цьому поверхня  піде в нескінченність. Згідно з теоремою єдиності (п.4.5) амплітуди полів
піде в нескінченність. Згідно з теоремою єдиності (п.4.5) амплітуди полів 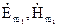 і
і 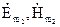 зменшуються при збільшенні відстані r від джерел швидше, ніж
зменшуються при збільшенні відстані r від джерел швидше, ніж 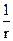 . Тоді
. Тоді 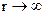 ліва частина рівняння (4.61) перетвориться в нуль. Оскільки вектор густини сторонніх струмів
ліва частина рівняння (4.61) перетвориться в нуль. Оскільки вектор густини сторонніх струмів 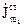 не дорівнює нулю тільки в об’ємі
не дорівнює нулю тільки в об’ємі  , а
, а 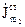 в
в 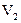 , то (4.69) буде мати вигляд:
, то (4.69) буде мати вигляд:
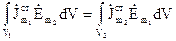 . (4.70)
. (4.70)
Вираз (4.70) – це математичне формулювання теореми взаємності. Фізичний зміст цієї теореми: поміняємо місцями стороні струми 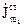 і
і 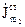 . Для цього будемо вважати, що
. Для цього будемо вважати, що 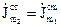 і
і 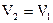 .
.

З теореми взаємності слідує, що в цьому випадку 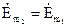 , тобто сторонній струм з густиною
, тобто сторонній струм з густиною 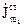 збуджував в
збуджував в 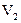 таке ж поле, яке він збуджує в об’ємі
таке ж поле, яке він збуджує в об’ємі  , якщо його помістити в об’єм
, якщо його помістити в об’єм 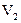 . Це доведення дуже важливе в теорії антен. Якщо є дві однакові антени І і ІІ з однаковим розподілом струмів, то можна стверджувати що антена І створює у антени ІІ таке ж поле, яке антена ІІ створює в антені І.
. Це доведення дуже важливе в теорії антен. Якщо є дві однакові антени І і ІІ з однаковим розподілом струмів, то можна стверджувати що антена І створює у антени ІІ таке ж поле, яке антена ІІ створює в антені І.
Теорема взаємності справедлива тільки в середовищах, які мають симетричні тензори діелектричної і магнітної проникності ( 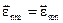 ,
,  ). Ця умова виконується для більшості кристалічних середовищ. У випадку гіротропних середовищ (наприклад, феритів) тензор
). Ця умова виконується для більшості кристалічних середовищ. У випадку гіротропних середовищ (наприклад, феритів) тензор  являється антисиметричним (
являється антисиметричним ( 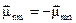 ). Тому для таких середовищ теорема взаємності несправедлива.
). Тому для таких середовищ теорема взаємності несправедлива.


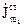 зосередженні в об’ємі
зосередженні в об’ємі  , а джерела з густиною струмів
, а джерела з густиною струмів 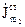 – в об’ємі
– в об’ємі 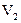 . Області об’ємів
. Області об’ємів  піде в нескінченність. Згідно з теоремою єдиності (п.4.5) амплітуди полів
піде в нескінченність. Згідно з теоремою єдиності (п.4.5) амплітуди полів 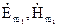 і
і 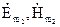 зменшуються при збільшенні відстані r від джерел швидше, ніж
зменшуються при збільшенні відстані r від джерел швидше, ніж 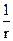 . Тоді
. Тоді 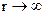 ліва частина рівняння (4.61) перетвориться в нуль. Оскільки вектор густини сторонніх струмів
ліва частина рівняння (4.61) перетвориться в нуль. Оскільки вектор густини сторонніх струмів 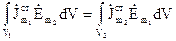 . (4.70)
. (4.70)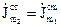 і
і 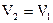 .
.
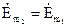 , тобто сторонній струм з густиною
, тобто сторонній струм з густиною 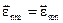 ,
,  ). Ця умова виконується для більшості кристалічних середовищ. У випадку гіротропних середовищ (наприклад, феритів) тензор
). Ця умова виконується для більшості кристалічних середовищ. У випадку гіротропних середовищ (наприклад, феритів) тензор  являється антисиметричним (
являється антисиметричним ( 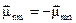 ). Тому для таких середовищ теорема взаємності несправедлива.
). Тому для таких середовищ теорема взаємності несправедлива.