Якщо в лінійному ізотропному середовищі система сторонніх джерел з густиною струмів 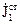 створює електромагнітне поле
створює електромагнітне поле 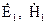 , а друга система з густиною струмів
, а друга система з густиною струмів 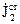 створює поле
створює поле 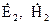 , то зв’язок між ними встановлює лема Лоренця. Вона дозволяє також розв’язувати задачі про збудження поля струмами складної конфігурації за заданими полями елементарного джерела.
, то зв’язок між ними встановлює лема Лоренця. Вона дозволяє також розв’язувати задачі про збудження поля струмами складної конфігурації за заданими полями елементарного джерела.
Запишемо рівняння Максвела для двох вказаних полів, джерела яких в загальному випадку не співпадають в просторі:

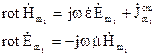
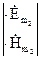
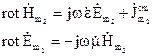
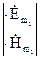
Помножимо скалярно записані рівняння згідно схемі, об’єднуючи їх попарно, віднімемо відповідні частині отриманих рівнянь. Отримаємо
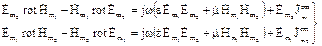 . (4.67)
. (4.67)
До лівих частин (4.67) застосуємо відому векторну тотожність, таким чином отримаємо
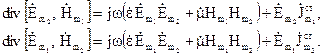
Для ізотропних середовищ немає різниці між 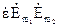 і
і 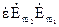 ,
,  і
і 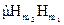 . Тоді віднявши почленно, отримаємо:
. Тоді віднявши почленно, отримаємо:
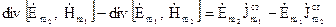 . (4.68)
. (4.68)
Вираз (4.68) – це диференціальна форма леми Лоренца.
Інтегруючи (4.68) по довільному об’єму і застосовуючи формулу Остроградського-Гауса, отримаємо інтегральну форму леми Лоренца:
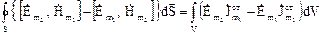 . (4.69)
. (4.69)
Це співвідношення дозволяє знаходити поле, яке створюється струмом з густиною 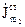 , якщо відоме поле, яке збуджується струмом з густиною
, якщо відоме поле, яке збуджується струмом з густиною 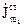 .
.
Векторні добутки 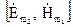 ,
, 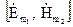 в лівій частині (4.61) можна розглядати як взаємні вектори Пойнтинга двох незалежних електромагнітних процесів.
в лівій частині (4.61) можна розглядати як взаємні вектори Пойнтинга двох незалежних електромагнітних процесів.
На основі леми Лоренца доводиться теорема взаємності, яка має фундаментальне значення, зокрема в теорії антен.


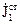 створює електромагнітне поле
створює електромагнітне поле 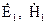 , а друга система з густиною струмів
, а друга система з густиною струмів 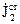 створює поле
створює поле 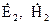 , то зв’язок між ними встановлює лема Лоренця. Вона дозволяє також розв’язувати задачі про збудження поля струмами складної конфігурації за заданими полями елементарного джерела.
, то зв’язок між ними встановлює лема Лоренця. Вона дозволяє також розв’язувати задачі про збудження поля струмами складної конфігурації за заданими полями елементарного джерела.
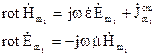
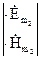
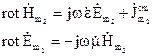
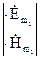
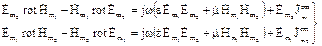 . (4.67)
. (4.67)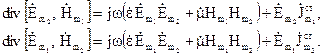
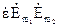 і
і 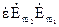 ,
,  і
і 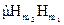 . Тоді віднявши почленно, отримаємо:
. Тоді віднявши почленно, отримаємо: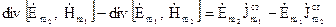 . (4.68)
. (4.68)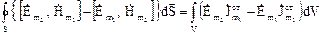 . (4.69)
. (4.69)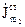 , якщо відоме поле, яке збуджується струмом з густиною
, якщо відоме поле, яке збуджується струмом з густиною 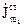 .
.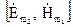 ,
, 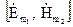 в лівій частині (4.61) можна розглядати як взаємні вектори Пойнтинга двох незалежних електромагнітних процесів.
в лівій частині (4.61) можна розглядати як взаємні вектори Пойнтинга двох незалежних електромагнітних процесів.