Рівняння Максвела являються диференційними рівняннями в частинних похідних і припускають безліч розв’язків. Щоб отримати єдиний розв’язок 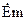 ,
,  необхідно, щоб ЕМП задовольняло не тільки рівнянням Максвела, але і деяким додатковим вимогам, які б однозначно визначали існування поля. Що це за вимоги і якими вони повинні бути, відповідає теорема єдиності.
необхідно, щоб ЕМП задовольняло не тільки рівнянням Максвела, але і деяким додатковим вимогам, які б однозначно визначали існування поля. Що це за вимоги і якими вони повинні бути, відповідає теорема єдиності.
При її доведенні розрізняють внутрішні і зовнішні задачі електродинаміки. Внутрішня задача – знаходиться ЕМП всередині V, обмеженого поверхнею S. Зовнішня задача – знаходиться ЕМП поза деяким об’ємом V.
Внутрішня задача електродинаміки. Теорема єдиності стверджує, що в середині області 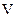 , обмеженої замкнутою поверхнею
, обмеженої замкнутою поверхнею  (рис. 4.4), розв’язок рівнянь Максвела для комплексних амплітуд
(рис. 4.4), розв’язок рівнянь Максвела для комплексних амплітуд
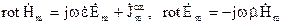 (4.58)
(4.58)
єдиний, якщо, по-перше, воно задовольняє одну з трьох крайових умов:
а) в кожній точці М поверхні S задана тангенціальна складова 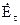 вектора
вектора 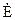 (
( 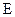 задача);
задача);
б) в кожній точці М поверхні S задана тангенціальна складова 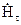 вектора
вектора 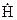 (
( 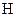 задача);
задача);
в) на одній частині поверхні 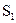 задана
задана 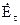 , а на решті частини
, а на решті частини 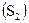 задана
задана 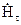 (
( 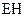 задача), причому
задача), причому 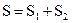
– і якщо, по-друге, при відсутності втрат 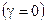 , частота
, частота 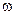 в (4.50) не співпадає ні з одною з резонансних частот в області V.
в (4.50) не співпадає ні з одною з резонансних частот в області V.
Припустимо, що існують два розв’язки поставленої задачі 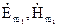 і
і 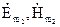 , які відповідають одному і тому ж розподілу густини стороннього струму
, які відповідають одному і тому ж розподілу густини стороннього струму 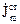 .
.
Підставивши їх в (4.58) будемо мати два варіанти запису рівнянь. Віднявши з першого друге рівняння, найдемо, що різниця розв’язків
 (4.59)
(4.59)
задовольняють однорідним рівнянням Максвела
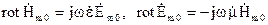 . (4.60)
. (4.60)
Величина 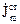 зникає, оскільки в обох варіантах фігурувала одна і таж задана величина
зникає, оскільки в обох варіантах фігурувала одна і таж задана величина 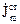 в(4.58).
в(4.58).
На поверхні  поле
поле 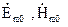 повинне задовольняти наступним граничним умовам:
повинне задовольняти наступним граничним умовам:
у випадку Е – задачі 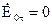 ; (4.61)
; (4.61)
у випадку Н – задачі 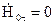 ; (4.62)
; (4.62)
у випадку Е Н – задачі 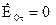 на
на 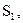 а
а 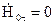 на
на  (4.63)
(4.63)
Рівняння балансу для активної потужності різниці поля 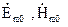 буде мати вигляд
буде мати вигляд
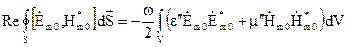 . (4.64)
. (4.64)
Якщо об’єм заповнений поглинаючим середовищем, тобто 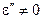 ,
, 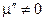 , то інтеграл з правої частини перетвориться в нуль, якщо
, то інтеграл з правої частини перетвориться в нуль, якщо 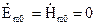 , тобто два розв’язки рівнянь Максвела співпадають у всьому об’ємі V. Тоді перетвориться в нуль і інтеграл в лівій частині (4.64). Це виникне, при
, тобто два розв’язки рівнянь Максвела співпадають у всьому об’ємі V. Тоді перетвориться в нуль і інтеграл в лівій частині (4.64). Це виникне, при 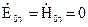 на всій поверхні S, або
на всій поверхні S, або 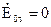 на частині поверхні
на частині поверхні 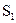 ; а на частині поверхні
; а на частині поверхні 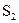
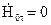 , тобто повинні бути задані дотичні складові електричного, або магнітного полів.
, тобто повинні бути задані дотичні складові електричного, або магнітного полів.
Отже, задача дійсно має один розв’язок :  і
і 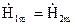 .
.
Якщо 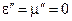 , то розв’язок буде нетривіальним, тобто не буде тотожно перетворюватися в нуль. Це свідчить про те, що в об’ємі
, то розв’язок буде нетривіальним, тобто не буде тотожно перетворюватися в нуль. Це свідчить про те, що в об’ємі 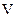 не виникає перетворення електромагнітної енергії в її інші види. В цьому випадку розв’язки рівнянь Максвела не являються єдиними.
не виникає перетворення електромагнітної енергії в її інші види. В цьому випадку розв’язки рівнянь Максвела не являються єдиними.
Зовнішня задача електродинаміки. В цьому випадку поверхні S не охоплює розглядувану частину простору, яка розповсюджується до нескінченості (рис. 4.5). Необхідно, крім перерахованих умов для єдиності розв’язку для внутрішньої задачі, знати додаткову умову, яка характеризує поведінку векторів 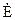 і
і 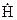 в точках, нескінченно віддалених від поверхні S.
в точках, нескінченно віддалених від поверхні S.
Подумки проведемо з довільної точки О в середині об’єму V сферу 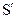 радіусу r так, щоб об’єм V і сторонні джерела
радіусу r так, щоб об’єм V і сторонні джерела 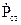 виявились в середині цієї сфери. Об’єм між S і
виявились в середині цієї сфери. Об’єм між S і 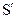 позначимо
позначимо  (рис. 4.5). Будемо шукати розв’язок рівнянь Максвела в середині цієї сфери
(рис. 4.5). Будемо шукати розв’язок рівнянь Максвела в середині цієї сфери 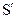 . Таким чином, зовнішня задача звелася до внутрішньої задачі електродинаміки. Для єдиності розв’язку необхідно, щоб всередині
. Таким чином, зовнішня задача звелася до внутрішньої задачі електродинаміки. Для єдиності розв’язку необхідно, щоб всередині 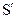
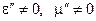 і
і
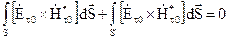 .
.
Так як сфера розташовується довільно, то треба щоб кожний з інтегралів дорівнював нулю. Щоб перший інтеграл дорівнював нулю, необхідно задавати дотичні складові 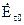 і
і 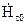 . Спрямувавши радіус сфери
. Спрямувавши радіус сфери 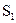 до нескінченності, з рівності нулю другого інтегралу отримаємо
до нескінченності, з рівності нулю другого інтегралу отримаємо
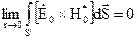 . (4.65)
. (4.65)
При 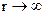 поверхня
поверхня 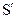 зростає пропорційно до
зростає пропорційно до 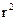 . Отже, щоб виконалась умова (4.65), необхідно, щоб абсолютна величина добутку
. Отже, щоб виконалась умова (4.65), необхідно, щоб абсолютна величина добутку  при
при 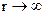 зменшувалась швидше, ніж
зменшувалась швидше, ніж  , тобто амплітуда векторів
, тобто амплітуда векторів 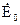 і
і 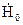 зменшувались швидше
зменшувались швидше 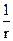 . Для цього достатньо, щоб невідомі величини
. Для цього достатньо, щоб невідомі величини 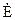 і
і 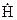 зменшувались швидше
зменшувались швидше 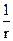 . Останнє завжди має місце, тобто в реальних середовищах існують втрати енергії.
. Останнє завжди має місце, тобто в реальних середовищах існують втрати енергії.
Таким чином, розв’язок зовнішньої задачі існує і в єдиному вигляді, якщо середовище, яке заповнює простір являється поглинаючим; на поверхні області, поза якою визначене поле, задані дотичні складові 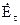 і
і 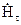 і електромагнітне поле задовольняє умові (4.57).
і електромагнітне поле задовольняє умові (4.57).
Для середовища без втрат теорему єдиності для зовнішньої задачі електродинаміки можна довести, якщо замість умови зменшення векторів 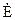 і
і 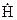 при
при 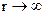 швидше
швидше 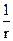 вимагати виконання наступних умов:
вимагати виконання наступних умов:
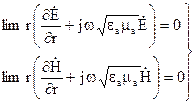 . (4.66)
. (4.66)
Співвідношення (4.58) називаються умовами випромінювання: при 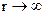 необхідно, щоб поле мало характер сферичних хвиль, які розходяться від джерела. Співвідношення (4.66) відомо ще як умова випромінювання Зомерфельда.
необхідно, щоб поле мало характер сферичних хвиль, які розходяться від джерела. Співвідношення (4.66) відомо ще як умова випромінювання Зомерфельда.


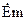 ,
,  необхідно, щоб ЕМП задовольняло не тільки рівнянням Максвела, але і деяким додатковим вимогам, які б однозначно визначали існування поля. Що це за вимоги і якими вони повинні бути, відповідає теорема єдиності.
необхідно, щоб ЕМП задовольняло не тільки рівнянням Максвела, але і деяким додатковим вимогам, які б однозначно визначали існування поля. Що це за вимоги і якими вони повинні бути, відповідає теорема єдиності.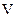 , обмеженої замкнутою поверхнею
, обмеженої замкнутою поверхнею  (рис. 4.4), розв’язок рівнянь Максвела для комплексних амплітуд
(рис. 4.4), розв’язок рівнянь Максвела для комплексних амплітуд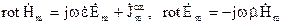 (4.58)
(4.58)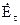 вектора
вектора 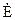 (
( 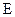 задача);
задача);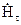 вектора
вектора 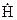 (
( 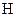 задача);
задача);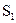 задана
задана 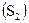 задана
задана 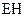 задача), причому
задача), причому 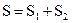
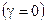 , частота
, частота 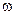 в (4.50) не співпадає ні з одною з резонансних частот в області V.
в (4.50) не співпадає ні з одною з резонансних частот в області V.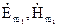 і
і 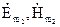 , які відповідають одному і тому ж розподілу густини стороннього струму
, які відповідають одному і тому ж розподілу густини стороннього струму 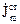 .
. (4.59)
(4.59)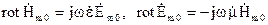 . (4.60)
. (4.60)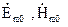 повинне задовольняти наступним граничним умовам:
повинне задовольняти наступним граничним умовам: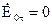 ; (4.61)
; (4.61)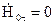 ; (4.62)
; (4.62)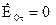 на
на 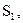 а
а  (4.63)
(4.63)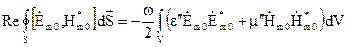 . (4.64)
. (4.64)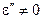 ,
, 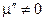 , то інтеграл з правої частини перетвориться в нуль, якщо
, то інтеграл з правої частини перетвориться в нуль, якщо 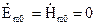 , тобто два розв’язки рівнянь Максвела співпадають у всьому об’ємі V. Тоді перетвориться в нуль і інтеграл в лівій частині (4.64). Це виникне, при
, тобто два розв’язки рівнянь Максвела співпадають у всьому об’ємі V. Тоді перетвориться в нуль і інтеграл в лівій частині (4.64). Це виникне, при 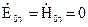 на всій поверхні S, або
на всій поверхні S, або 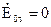 на частині поверхні
на частині поверхні 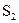
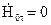 , тобто повинні бути задані дотичні складові електричного, або магнітного полів.
, тобто повинні бути задані дотичні складові електричного, або магнітного полів. і
і 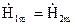 .
.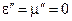 , то розв’язок буде нетривіальним, тобто не буде тотожно перетворюватися в нуль. Це свідчить про те, що в об’ємі
, то розв’язок буде нетривіальним, тобто не буде тотожно перетворюватися в нуль. Це свідчить про те, що в об’ємі 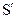 радіусу r так, щоб об’єм V і сторонні джерела
радіусу r так, щоб об’єм V і сторонні джерела 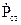 виявились в середині цієї сфери. Об’єм між S і
виявились в середині цієї сфери. Об’єм між S і  (рис. 4.5). Будемо шукати розв’язок рівнянь Максвела в середині цієї сфери
(рис. 4.5). Будемо шукати розв’язок рівнянь Максвела в середині цієї сфери 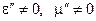 і
і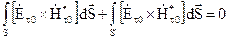 .
.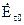 і
і 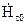 . Спрямувавши радіус сфери
. Спрямувавши радіус сфери 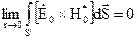 . (4.65)
. (4.65)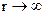 поверхня
поверхня 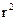 . Отже, щоб виконалась умова (4.65), необхідно, щоб абсолютна величина добутку
. Отже, щоб виконалась умова (4.65), необхідно, щоб абсолютна величина добутку  при
при  , тобто амплітуда векторів
, тобто амплітуда векторів 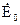 і
і 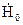 зменшувались швидше
зменшувались швидше 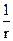 . Для цього достатньо, щоб невідомі величини
. Для цього достатньо, щоб невідомі величини 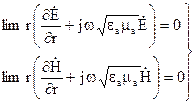 . (4.66)
. (4.66)