У будь-якій задачі електромагнітне поле тим або іншим чином обмежене у просторі. Природними межами можуть бути, наприклад, металеві стінки, або межа розділу між середовищами з різними параметрами. Якщо параметри середовищ на межі розділу змінюються стрибком, то і компоненти векторів ЕМП теж мають розрив в точках межі. Необхідно знайти зв’язок між векторами ЕМП на межі, які б задовольняли рівнянням Максвела.
Математична постановка задачі. Нехай поверхня  розділяє середовища 1
розділяє середовища 1 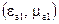 і 2
і 2 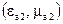 . Виберемо на
. Виберемо на  точку М і виділимо в її околі малий елемент поверхні
точку М і виділимо в її околі малий елемент поверхні 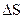 , вважаючи його плоским (рис. 3.1). До точки М проведемо орт нормалі
, вважаючи його плоским (рис. 3.1). До точки М проведемо орт нормалі 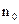 (напрямок з середовища 2 в 1). На
(напрямок з середовища 2 в 1). На 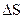 можна провести безліч дотичних ортів. Виберемо з них два ортогональних
можна провести безліч дотичних ортів. Виберемо з них два ортогональних  і
і 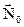 . При цьому отримуємо трійку векторів
. При цьому отримуємо трійку векторів 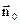 ,
,  ,
, 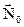 за якими можна розкласти будь-який з векторів
за якими можна розкласти будь-який з векторів  ,
, 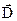 ,
,  ,
, 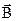 в точці М. Якщо вектор
в точці М. Якщо вектор  вибраний так, що він співпадає з проекцією деякого вектора
вибраний так, що він співпадає з проекцією деякого вектора 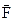 на
на 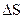 , то маємо розкладення
, то маємо розкладення
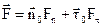 , (3.1)
, (3.1)
де 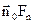 – нормальна,
– нормальна,
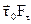 – дотична компонента вектора
– дотична компонента вектора 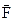 .
.
Орти 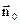 ,
,  ,
, 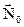 утворюють праву трійку векторів і зв’язані співвідношенням
утворюють праву трійку векторів і зв’язані співвідношенням
 (3.2)
(3.2)
Межа розділу середовищ, яка розглядається – це поверхня, на якій параметри eа, mа, g (принаймні один з них) мають розрив як функції нормалі. Тому компоненти векторів поля при переході межі розділу теж матимуть розриви: або обидві компоненти поля, або одна з них змінюватиметься стрибком. Тоді векторна лінія матиме перегин. На межі перехід від  до
до 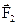 приходять зі зміною абсолютної величині і напрямку вектора (рис. 3.2 а, б).
приходять зі зміною абсолютної величині і напрямку вектора (рис. 3.2 а, б).
В точках розриву застосування диференційних рівнянь Максвела неможливе. Тому звернемося до інтегральних виразів цих рівнянь і отримаємо важливі співвідношення, які називаються граничними умовами.


 розділяє середовища 1
розділяє середовища 1 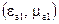 і 2
і 2 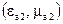 . Виберемо на
. Виберемо на 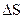 , вважаючи його плоским (рис. 3.1). До точки М проведемо орт нормалі
, вважаючи його плоским (рис. 3.1). До точки М проведемо орт нормалі 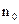 (напрямок з середовища 2 в 1). На
(напрямок з середовища 2 в 1). На  і
і 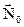 . При цьому отримуємо трійку векторів
. При цьому отримуємо трійку векторів 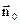 ,
,  ,
, 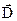 ,
,  ,
, 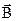 в точці М. Якщо вектор
в точці М. Якщо вектор 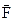 на
на 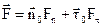 , (3.1)
, (3.1)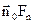 – нормальна,
– нормальна,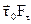 – дотична компонента вектора
– дотична компонента вектора  (3.2)
(3.2) до
до 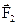 приходять зі зміною абсолютної величині і напрямку вектора (рис. 3.2 а, б).
приходять зі зміною абсолютної величині і напрямку вектора (рис. 3.2 а, б).