Система рівнянь Максвела охоплює сукупність електромагнітних явищ. В ряді випадків ці рівняння спрощуються.
У самому простому випадку електромагнітне поле не залежить від часу і, крім цього, відсутнє переміщення зарядів  . Система рівнянь Максвела (див. рівняння 1-8 в табл. 2.1 в. 2.1) в цьому випадку розпадаються на дві незалежні системи
. Система рівнянь Максвела (див. рівняння 1-8 в табл. 2.1 в. 2.1) в цьому випадку розпадаються на дві незалежні системи
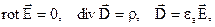 (2.81)
(2.81)
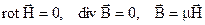 . (2.82)
. (2.82)
Система рівнянь (2.81) має тільки електричні величини, а система (2.82) – тільки магнітні. Тобто, для цього випадку електричні і магнітні поля незалежні.
Явища, які описуються рівняннями (2.81) називаються електростатичними, а система – повною системою диференціальних рівнянь електростатики. Електростатичні поля – це поля, які створюються нерухомими, незмінними по величині зарядами.
Рівняння (2.82) складають повну систему диференційних рівнянь магнітостатики. Явища, які описуються (2.82), називаються магнітостатичними. Рівняння магнітостатики використовуються для аналізу властивостей магнітного поля, яке може бути створене сталим струмом в області де 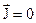 .
.
Якщо 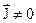 , електричні і магнітні поля не можна вважати незалежними. Електромагнітне поле, яке створюється сталими струмами, називають стаціонарним електромагнітним полем. Система рівнянь для цього випадку має вигляд:
, електричні і магнітні поля не можна вважати незалежними. Електромагнітне поле, яке створюється сталими струмами, називають стаціонарним електромагнітним полем. Система рівнянь для цього випадку має вигляд:
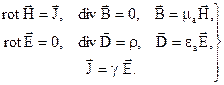 (2.83)
(2.83)
Виділяється самостійний клас – квазістаціонарні процеси, тобто процеси, які протікають достатньо повільно. В цьому випадку перше рівняння Максвела можна записати в двох варіантах:
а) якщо 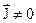 , то можна знехтувати
, то можна знехтувати 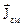 , тоді
, тоді
 ;
;
б) якщо 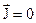 , (конденсатор в колі змінного струму), то струми зміщення враховуються, при цьому перше рівняння запишеться
, (конденсатор в колі змінного струму), то струми зміщення враховуються, при цьому перше рівняння запишеться
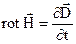 .
.
В загальному випадку використовується повна система рівнянь Максвела (див. табл. 2.1 в 2.1).
У випадку гармонічних коливань систему рівнянь Максвела, без матеріальних рівнянь, можна представити системою (2.79) в 2.13.
3 Поля на межі розділу середовищ (граничні умови для векторів електромагнітного поля 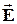 ,
, 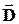 ,
, 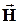 ,
, 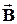 )
)


 . Система рівнянь Максвела (див. рівняння 1-8 в табл. 2.1 в. 2.1) в цьому випадку розпадаються на дві незалежні системи
. Система рівнянь Максвела (див. рівняння 1-8 в табл. 2.1 в. 2.1) в цьому випадку розпадаються на дві незалежні системи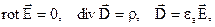 (2.81)
(2.81)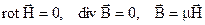 . (2.82)
. (2.82)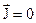 .
.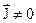 , електричні і магнітні поля не можна вважати незалежними. Електромагнітне поле, яке створюється сталими струмами, називають стаціонарним електромагнітним полем. Система рівнянь для цього випадку має вигляд:
, електричні і магнітні поля не можна вважати незалежними. Електромагнітне поле, яке створюється сталими струмами, називають стаціонарним електромагнітним полем. Система рівнянь для цього випадку має вигляд: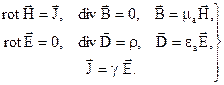 (2.83)
(2.83)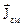 , тоді
, тоді ;
;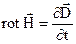 .
.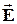 ,
, 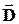 ,
, 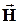 ,
, 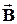 )
)