Рівняння Максвела – це лінійні диференціальні рівняння. Тому, при вивчені гармонічних полів, замість векторів  і
і  можна розглядати комплексні вектори.
можна розглядати комплексні вектори.
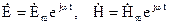 , (2.61)
, (2.61)
які зв’язані з векторами  і
і  співвідношенням
співвідношенням
 . (2.62)
. (2.62)
Якщо електричний вектор  заданий у вигляді
заданий у вигляді
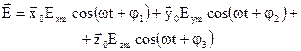 , (2.63)
, (2.63)
то комплексна амплітуда 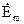 буде мати вид
буде мати вид
 . (2.64)
. (2.64)
Якщо всі складові змінюються по фазі, то запис спрощується, наприклад,
 , то
, то 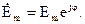 (2.65)
(2.65)
Аналогічний запис можна зробити і для вектора  :
: 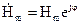 .
.
Перейдемо до комплексних зображень рівнянь Максвела. Перше рівняння Максвела в комплексній формі приймає вид
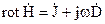 . (2.66)
. (2.66)
Враховуючи, що
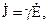 а
а 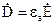 ,
,
отримаємо
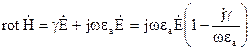 . (2.67)
. (2.67)
Введемо позначення
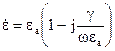 (2.68)
(2.68)
і перепишемо рівняння (2.67) в формі
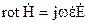 . (2.69)
. (2.69)
Величина  в (2.69) характеризує електричні властивості середовища і називається комплексною діелектричною проникністю середовища. Її значення залежить від частоти. Величина
в (2.69) характеризує електричні властивості середовища і називається комплексною діелектричною проникністю середовища. Її значення залежить від частоти. Величина 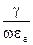 дорівнює відношенню амплітуд густин струму провідності і струму зміщення, і називається тангенсом кута втрат (рис. 2.9):
дорівнює відношенню амплітуд густин струму провідності і струму зміщення, і називається тангенсом кута втрат (рис. 2.9):
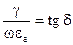 . (2.70)
. (2.70)
Тоді
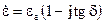 . (2.71)
. (2.71)
В загальному випадку комплексну діелектричну проникність середовища можна записати:
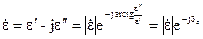 , (2.72)
, (2.72)
де 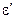 і
і 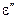 – дійсні числа.
– дійсні числа.
Вираз (2.72) дозволяє врахувати залежність електричних властивостей речовини від частоти, тобто її дисперсію. Одночасно враховується явище запізнення вектора  відносно вектора
відносно вектора  в високочастотних електричних полях (діелектричний гістерезис), а також залежність провідності речовини від частоти.
в високочастотних електричних полях (діелектричний гістерезис), а також залежність провідності речовини від частоти.
В загальному випадку
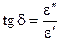 . (2.73)
. (2.73)
З урахуванням цього зауваження, критерій класифікації середовищ можна записати
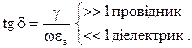 (2.74)
(2.74)
З співвідношення для 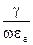 бачимо, що діелектричні властивості сильніше проявляються на більш високих частотах. Метали мають велику питому провідність. Наприклад, холоднокачана мідь має
бачимо, що діелектричні властивості сильніше проявляються на більш високих частотах. Метали мають велику питому провідність. Наприклад, холоднокачана мідь має 
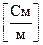 , залізо –
, залізо – 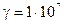
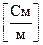 .
.
У типових діелектриків, навпаки 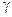 дуже мала. Наприклад, у кварцу
дуже мала. Наприклад, у кварцу 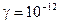
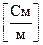 .
.
Існує ряд середовищ, які займають проміжне положення між провідниками і діелектриками, наприклад, вода, грунт і ін.
Наприклад,
у дистильованої води 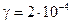
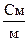 ;
;
у сухого грунту 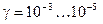
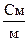 ;
;
у морської води 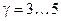
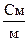 ;
;
у вологого грунту 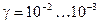
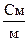 .
.
Такі середовища на одних частотах поводять себе як провідники 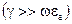 , а на інших – діелектрики
, а на інших – діелектрики  .
.
Розглянемо друге рівняння Максвела. В загальному випадку, при переході до комплексних векторів, магнітну проникність середовища також треба вважати комплексною величиною:
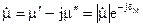 . (2.75)
. (2.75)
Кут 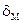 характеризує відставання по фазі вектора
характеризує відставання по фазі вектора 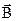 від вектора
від вектора  , наприклад, у феромагнетиках (явище гістерезису).
, наприклад, у феромагнетиках (явище гістерезису).
З урахуванням цього, друге рівняння Максвела можна записати
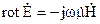 . (2.76)
. (2.76)
Третє і четверте рівняння є наслідком перших двох: (2.69) і (2.70). Взявши дивергенцію від обох частин цих рівнянь, отримуємо
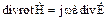 , через те, що
, через те, що 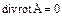 , то
, то  . (2.77)
. (2.77)
Аналогічно,
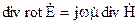 , то
, то 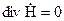 . (2.78)
. (2.78)
Таким чином, гармонічні поля описуються системою рівнянь
 (2.79)
(2.79)
Система рівнянь Максвела, яка враховує сторонні струми і заряди, у випадку гармонічних полів має вигляд
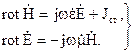 (2.80)
(2.80)


 і
і  можна розглядати комплексні вектори.
можна розглядати комплексні вектори.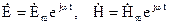 , (2.61)
, (2.61) . (2.62)
. (2.62)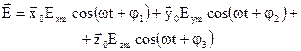 , (2.63)
, (2.63)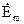 буде мати вид
буде мати вид . (2.64)
. (2.64) , то
, то 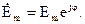 (2.65)
(2.65)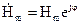 .
.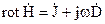 . (2.66)
. (2.66)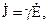 а
а 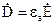 ,
,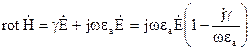 . (2.67)
. (2.67)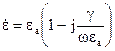 (2.68)
(2.68)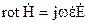 . (2.69)
. (2.69) в (2.69) характеризує електричні властивості середовища і називається комплексною діелектричною проникністю середовища. Її значення залежить від частоти. Величина
в (2.69) характеризує електричні властивості середовища і називається комплексною діелектричною проникністю середовища. Її значення залежить від частоти. Величина 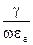 дорівнює відношенню амплітуд густин струму провідності і струму зміщення, і називається тангенсом кута втрат (рис. 2.9):
дорівнює відношенню амплітуд густин струму провідності і струму зміщення, і називається тангенсом кута втрат (рис. 2.9):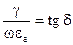 . (2.70)
. (2.70)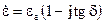 . (2.71)
. (2.71)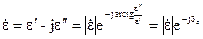 , (2.72)
, (2.72)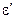 і
і 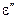 – дійсні числа.
– дійсні числа.
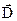 відносно вектора
відносно вектора 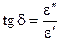 . (2.73)
. (2.73)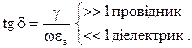 (2.74)
(2.74)
 , залізо –
, залізо – 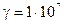
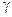 дуже мала. Наприклад, у кварцу
дуже мала. Наприклад, у кварцу 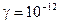
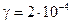
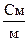 ;
;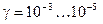
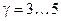
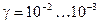
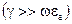 , а на інших – діелектрики
, а на інших – діелектрики  .
.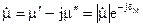 . (2.75)
. (2.75)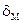 характеризує відставання по фазі вектора
характеризує відставання по фазі вектора 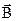 від вектора
від вектора 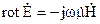 . (2.76)
. (2.76)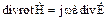 , через те, що
, через те, що 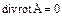 , то
, то  . (2.77)
. (2.77)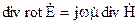 , то
, то 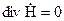 . (2.78)
. (2.78) (2.79)
(2.79)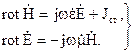 (2.80)
(2.80)