Всі реальні електромагнітні процеси можна представити або у вигляді суми дискретних гармонічних коливань, або у вигляді неперервного спектра гармонічних коливань. Такі представлення мають великий практичний і теоретичний інтерес і поля називають монохроматичними (однокольоровими). Назву запозичено з оптики: кожному кольору відповідає коливання певної частоти.
Аналіз гармонічних коливань значно спрощується при використані методу комплексних амплітуд, суть якого полягає в наступному: замість будь-якої скалярної функції 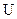 , яка змінюється по закону
, яка змінюється по закону
 , (2.45)
, (2.45)
де 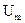 – амплітуда,
– амплітуда,
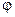 – початкова фаза коливань,
– початкова фаза коливань,
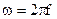 – циклічна частота гармонічного коливання, вводиться в розгляд комплексна функція:
– циклічна частота гармонічного коливання, вводиться в розгляд комплексна функція:
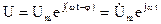 . (2.46)
. (2.46)
Величину 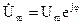 називають комплексною амплітудою функції
називають комплексною амплітудою функції 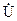 .
.
Для переходу від комплексної функції 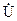 до початкової
до початкової 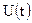 треба взяти від
треба взяти від 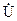 реальну частину
реальну частину
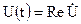 . (2.47)
. (2.47)
Аналогічно, замість вектора
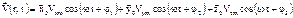 (2.48)
(2.48)
можна ввести до розгляду комплексний вектор
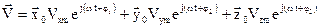 . (2.49)
. (2.49)
Вираз (2.49) можна переписати у вигляді
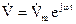 , (2.50)
, (2.50)
де
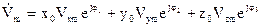 (2.51)
(2.51)
– комплексна амплітуда вектора 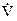 .
.
Для переходу до початкового вектора необхідно взяти реальну частину від 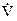
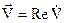 . (2.52)
. (2.52)
Якщо функції 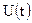 і
і 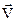 задовольняють лінійним диференційним рівнянням, то їм також задовольняють відповідні комплексні функції
задовольняють лінійним диференційним рівнянням, то їм також задовольняють відповідні комплексні функції 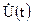 і
і 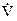 .
.
Визначення комплексних функцій простіше визначення початкових. Це пояснюється тим, що диференціювання комплексної функції за часом рівносильне множенню на 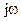 , а інтегрування по часі – діленню на
, а інтегрування по часі – діленню на 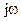 .
.
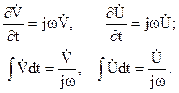
Запишемо співвідношення, яке витікає з формули Ейлера
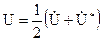 . (2.53)
. (2.53)


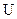 , яка змінюється по закону
, яка змінюється по закону , (2.45)
, (2.45)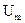 – амплітуда,
– амплітуда,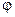 – початкова фаза коливань,
– початкова фаза коливань,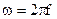 – циклічна частота гармонічного коливання, вводиться в розгляд комплексна функція:
– циклічна частота гармонічного коливання, вводиться в розгляд комплексна функція: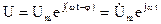 . (2.46)
. (2.46)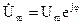 називають комплексною амплітудою функції
називають комплексною амплітудою функції 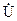 .
.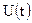 треба взяти від
треба взяти від 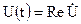 . (2.47)
. (2.47)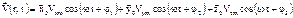 (2.48)
(2.48)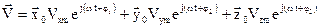 . (2.49)
. (2.49)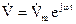 , (2.50)
, (2.50)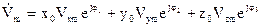 (2.51)
(2.51)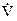 .
.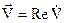 . (2.52)
. (2.52)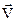 задовольняють лінійним диференційним рівнянням, то їм також задовольняють відповідні комплексні функції
задовольняють лінійним диференційним рівнянням, то їм також задовольняють відповідні комплексні функції 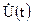 і
і 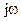 , а інтегрування по часі – діленню на
, а інтегрування по часі – діленню на 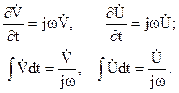
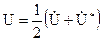 . (2.53)
. (2.53)