При розгляді системи рівнянь Максвела в диференційній формі разом з матеріальними рівняннями, під вектором 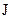 мали на увазі густину струму провідності, який виникає в провідному середовищі під дією електричного поля. Цей вектор задовольняє диференційному закону Ома:
мали на увазі густину струму провідності, який виникає в провідному середовищі під дією електричного поля. Цей вектор задовольняє диференційному закону Ома: 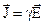 .
.
Крім цього струму в області простору, що вивчається, можуть існувати струми, які розглядаються як першопричина виникнення електричного поля і вважаються заданими. Ці струми прийнято називати сторонніми.
Особливо важливу роль відіграють сторонні струми при вивченні випромінювання ЕМХ різноманітними антенами.
Для врахування сторонніх струмів необхідно перше рівняння Максвела представити у вигляді
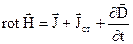 , (2.42)
, (2.42)
де 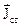 – густина сторонніх струмів в точці простору, що розглядається.
– густина сторонніх струмів в точці простору, що розглядається.
При розгляді багатьох питань, замість сторонніх струмів, задаються сторонньою напруженістю електричного поля 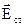 . Під
. Під 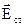 розуміють напруженість електричного поля, яка створюється зарядами і струмами, розташованими за межами області, яка розглядається.
розуміють напруженість електричного поля, яка створюється зарядами і струмами, розташованими за межами області, яка розглядається.
Введення 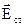 і
і 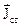 спрощує задачу, яка розв’язується. Фактично воно виключає детальний аналіз процесів, які проходять в якій-небудь частині простору. Аналогічно до сторонніх струмів вводиться поняття сторонніх зарядів. Тоді третє рівняння Максвела записується у вигляді
спрощує задачу, яка розв’язується. Фактично воно виключає детальний аналіз процесів, які проходять в якій-небудь частині простору. Аналогічно до сторонніх струмів вводиться поняття сторонніх зарядів. Тоді третє рівняння Максвела записується у вигляді
 , (2.43)
, (2.43)
де 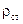 – об’ємна густина сторонніх зарядів.
– об’ємна густина сторонніх зарядів.
У випадку змінних процесів, сторонні струми і заряди пов’язані рівнянням неперервності
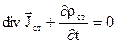 . (2.44)
. (2.44)


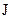 мали на увазі густину струму провідності, який виникає в провідному середовищі під дією електричного поля. Цей вектор задовольняє диференційному закону Ома:
мали на увазі густину струму провідності, який виникає в провідному середовищі під дією електричного поля. Цей вектор задовольняє диференційному закону Ома: 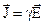 .
.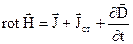 , (2.42)
, (2.42)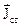 – густина сторонніх струмів в точці простору, що розглядається.
– густина сторонніх струмів в точці простору, що розглядається.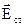 . Під
. Під  , (2.43)
, (2.43)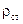 – об’ємна густина сторонніх зарядів.
– об’ємна густина сторонніх зарядів.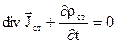 . (2.44)
. (2.44)