
Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Третє рівняння Максвела (узагальнена теорема Гауса)Дата додавання: 2014-10-07; переглядів: 1222.
|
Онлайн система числення Калькулятор онлайн звичайний Науковий калькулятор онлайн
| ||||||||||||||||

 і величиною заряду, який його породжує. Розглянемо деякий об’єм
і величиною заряду, який його породжує. Розглянемо деякий об’єм 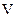 , обмежений замкненою поверхнею
, обмежений замкненою поверхнею  (рис. 2.4, а). В середині об’єму знаходиться електричний заряд
(рис. 2.4, а). В середині об’єму знаходиться електричний заряд 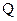 . Математично теорема Гауса формулюється
. Математично теорема Гауса формулюється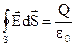 . (2.23)
. (2.23)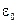 . Якщо заряд розподілений неперервно, то
. Якщо заряд розподілений неперервно, то  , (2.24)
, (2.24)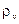 – об’ємна густина заряду.
– об’ємна густина заряду.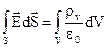 , (2.25)
, (2.25)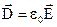 :
: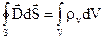 . (2.26)
. (2.26)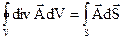 , (2.27)
, (2.27)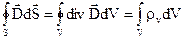 . (2.28)
. (2.28)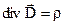 . (2.29)
. (2.29)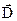 відміна від нуля тільки в тих точках простору, де є вільні заряди. В цих точках лінії вектора
відміна від нуля тільки в тих точках простору, де є вільні заряди. В цих точках лінії вектора 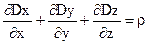 . (2.30)
. (2.30)