Друге рівняння є узагальненням закону індукції Фарадея: якщо замкнений контур  пронизується змінним струмом
пронизується змінним струмом 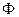 , то в контурі виникає ЕРС, яка дорівнює швидкості зміни магнітного потоку (рис. 2.3):
, то в контурі виникає ЕРС, яка дорівнює швидкості зміни магнітного потоку (рис. 2.3):
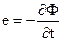 . (2.15)
. (2.15)
Знак “мінус” в правій частині (2.15) означає, що ЕРС нібито прагне перешкодити зміні потоку 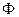 , який пронизує цей контур. Це положення відоме як “правило Лоренца”. Це рівняння справедливо тільки для провідного контуру. Максвел припустив, що це рівняння справедливе також і в тому випадку, якщо середовище не має провідність. Відомо, що будь-яка ЕРС, яка наводиться на контур і, дорівнює циркуляції вектора
, який пронизує цей контур. Це положення відоме як “правило Лоренца”. Це рівняння справедливо тільки для провідного контуру. Максвел припустив, що це рівняння справедливе також і в тому випадку, якщо середовище не має провідність. Відомо, що будь-яка ЕРС, яка наводиться на контур і, дорівнює циркуляції вектора  по цьому контуру:
по цьому контуру:
 . (2.16)
. (2.16)
Магнітний струм 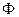 зв’язаний з вектором
зв’язаний з вектором 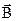 співвідношенням
співвідношенням
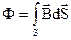 , (2.17)
, (2.17)
де  – довільна поверхня, яка опирається на контур
– довільна поверхня, яка опирається на контур  ;
;
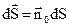 ,
, 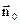 – орт нормалі до поверхні
– орт нормалі до поверхні  , який утворює правогвинтову систему з обходом контуру (2.13).
, який утворює правогвинтову систему з обходом контуру (2.13).
Підставляючи формули (2.17) і (2.16) в (2.15), отримуємо
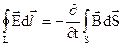 . (2.18)
. (2.18)
Це співвідношення (2.18) придатне для контуру скінчених розмірів і називається другим рівнянням Максвела в інтегральній формі.
Диференційна форма. Якщо вважати, що контур нерухомий і не змінюється з часом, тоді можливо похідну по часі внести під знак інтеграла (2.18)
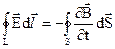 . (2.19)
. (2.19)
Застосовуючи теорему Стокса
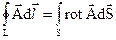 ,
,
можна переписати (2.19) у вигляді
 . (2.20)
. (2.20)
Через те, що  – довільна поверхня, то (2.20) виконується у випадку, якщо
– довільна поверхня, то (2.20) виконується у випадку, якщо
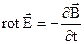 . (2.21)
. (2.21)
Співвідношення (2.21) – це диференційна форма другого рівняння Максвела.
В прямокутній системі координат 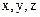 отримуємо три скалярних рівняння:
отримуємо три скалярних рівняння:
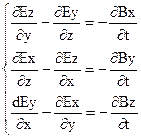 . (2.22)
. (2.22)
З (2.21) слідує, що ротор напруженості електричного поля  в будь-який його точці дорівнює по величині і протилежний за знаком швидкості зміни індукції
в будь-який його точці дорівнює по величині і протилежний за знаком швидкості зміни індукції 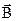 в цій точці.
в цій точці.


 пронизується змінним струмом
пронизується змінним струмом 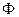 , то в контурі виникає ЕРС, яка дорівнює швидкості зміни магнітного потоку (рис. 2.3):
, то в контурі виникає ЕРС, яка дорівнює швидкості зміни магнітного потоку (рис. 2.3):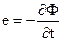 . (2.15)
. (2.15) по цьому контуру:
по цьому контуру: . (2.16)
. (2.16)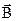 співвідношенням
співвідношенням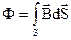 , (2.17)
, (2.17) – довільна поверхня, яка опирається на контур
– довільна поверхня, яка опирається на контур 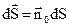 ,
, 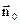 – орт нормалі до поверхні
– орт нормалі до поверхні 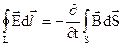 . (2.18)
. (2.18)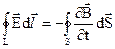 . (2.19)
. (2.19)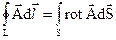 ,
, . (2.20)
. (2.20)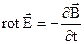 . (2.21)
. (2.21)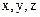 отримуємо три скалярних рівняння:
отримуємо три скалярних рівняння: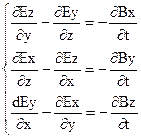 . (2.22)
. (2.22) в будь-який його точці дорівнює по величині і протилежний за знаком швидкості зміни індукції
в будь-який його точці дорівнює по величині і протилежний за знаком швидкості зміни індукції