Датський фізик Ерстед встановив експериментальний факт, що протікання струму по провідниках приводить до виникнення магнітного поля. Французький фізик Ампер на основі відкриття Ерстеда сформулював закон повного струму, який називається законом Ампера.
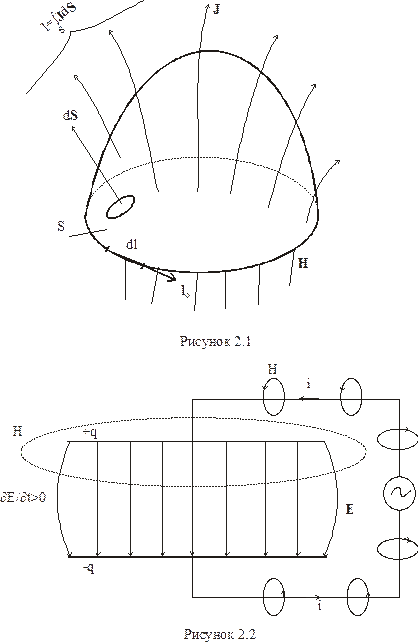
Інтегральна форма закону Ампера: розглянемо в просторі контур  , обмежений поверхнею
, обмежений поверхнею  (рис. 3.1). Напрям обходу контуру вибираємо таким чином, щоб під час руху вздовж контуру з кінця вектора елементарної площинки
(рис. 3.1). Напрям обходу контуру вибираємо таким чином, щоб під час руху вздовж контуру з кінця вектора елементарної площинки 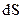 , він був проти часової стрілки. Припустимо, що поверхня
, він був проти часової стрілки. Припустимо, що поверхня  пронизується деякою системою струмів, розподілених в просторі неперервно з деякою об’ємною густиною
пронизується деякою системою струмів, розподілених в просторі неперервно з деякою об’ємною густиною 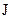 . Тоді повний струм, який пронизує контур, визначиться у вигляді:
. Тоді повний струм, який пронизує контур, визначиться у вигляді:
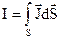 . (2.1)
. (2.1)
Закон повного струму: циркуляція по контуру  напруженості магнітного поля
напруженості магнітного поля 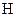 , спричинена протіканням
, спричинена протіканням 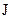 , дорівнює повному струму
, дорівнює повному струму
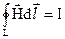 . (2.2)
. (2.2)
Підставимо формулу (2.2) в (2.1), і тоді отримуємо інтегральну форму закону Ампера
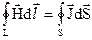 . (2.3)
. (2.3)
Диференційна форма закону Ампера. Якщо скористатися теоремою Стокса для будь-якого векторного поля
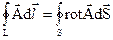 , (2.4)
, (2.4)
і з її допомогою перетворити вираз (2.3), то будемо мати:
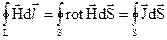 , (2.5)
, (2.5)
через те, що контур довільний, то рівність (2.5) можлива при умові:
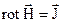 . (2.6)
. (2.6)
Рівняння (2.6) це – диференційна форма закону Ампера. Закон Ампера справедливий у випадку постійних процесів і виявляється невірним у випадку змінних процесів. Максвел дав узагальнююче формулювання закону повного струму. Він ввів поняття струму зміщення, який з точки зору утворення магнітного поля, рівноцінний струму провідності.
Прикладом системи зі струмами зміщення може бути конденсатор в колі змінного струму (рис. 2.2). Змінний електричний струм протікає по замкнутому колу, в якому є конденсатор, незважаючи на те, що між обкладинками відсутні носії електричного заряду. Тобто там протікає якийсь струм по природі відмінний від струму провідності. Цей струм називається струмом зміщення. З’єднувальний провід оточений кільцевими лініями магнітного поля. Максвел припустив, що вони не обриваються у пластин конденсатора, а утворюють замкнену поверхню, тобто змінне електричне поле також
оточене магнітним полем. Це дало основу для введення поняття про новий вид струму – струму зміщення Jзм 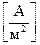 .
.
Густина струму зміщення визначається формулою:
 . (2.7)
. (2.7)
Підкреслимо: струм провідності – впорядкований рух вільних електричних зарядів. Струм зміщення – відповідає тільки зміні електричного поля і не супроводжується яким-небудь рухом електричних зарядів.
У вакуумі 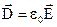 і (2.7) приймає вид:
і (2.7) приймає вид:
 . (2.8)
. (2.8)
Струм зміщення у вакуумі не супроводжується зміною тепла.
І так, у випадку змінного поля, Максвел запропонував додати у праву частину закону Ампера струм зміщення, щоб він був вірний для цього. Тоді
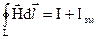 . (2.9)
. (2.9)
Струм зміщення виражається через густину струму зміщення
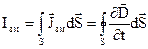 . (2.10)
. (2.10)
Тепер, якщо підставити (2.10), (2.1) в (2.9), отримуємо
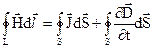 . (2.11)
. (2.11)
Рівняння (2.11) сформульоване для контуру скінчених розмірів. Це перше рівняння Максвела в інтегральній формі.
Для переходу до диференційної форми, необхідно скористатися теоремою Стокса. Тоді отримуємо:
 . (2.12)
. (2.12)
Через те, що  – довільна поверхня, то (2.12) можливо тільки в тому випадку, якщо
– довільна поверхня, то (2.12) можливо тільки в тому випадку, якщо
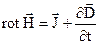 . (2.13)
. (2.13)
Рівняння (2.13) – це диференційна форма першого рівняння Максвела.
Вираз (2.13) встановлює внутрішній взаємозв’язок електричного і магнітного поля. Зміна в часі електричного поля в який-небудь точці простору приводить до виникнення струму зміщення, який викликає появу змінного магнітного поля.
Векторне рівняння (2.13) в диференційній формі еквівалентне трьом скалярним рівнянням, які в декартовій системі координат мають вигляд:
 (2.14)
(2.14)


 , обмежений поверхнею
, обмежений поверхнею  (рис. 3.1). Напрям обходу контуру вибираємо таким чином, щоб під час руху вздовж контуру з кінця вектора елементарної площинки
(рис. 3.1). Напрям обходу контуру вибираємо таким чином, щоб під час руху вздовж контуру з кінця вектора елементарної площинки 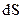 , він був проти часової стрілки. Припустимо, що поверхня
, він був проти часової стрілки. Припустимо, що поверхня 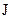 . Тоді повний струм, який пронизує контур, визначиться у вигляді:
. Тоді повний струм, який пронизує контур, визначиться у вигляді: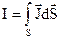 . (2.1)
. (2.1)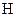 , спричинена протіканням
, спричинена протіканням 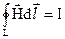 . (2.2)
. (2.2)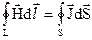 . (2.3)
. (2.3)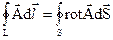 , (2.4)
, (2.4)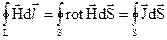 , (2.5)
, (2.5)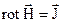 . (2.6)
. (2.6)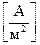 .
. . (2.7)
. (2.7)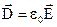 і (2.7) приймає вид:
і (2.7) приймає вид: . (2.8)
. (2.8)
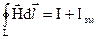 . (2.9)
. (2.9)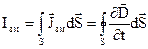 . (2.10)
. (2.10)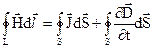 . (2.11)
. (2.11) . (2.12)
. (2.12)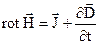 . (2.13)
. (2.13) (2.14)
(2.14)