Взаємодія між зарядженими частинками здійснюється через ЕМП, яке вважається визначеним, якщо в кожній точці простору відомі величини і напрям чотирьох векторів:  – напруженості електричного поля;
– напруженості електричного поля; 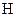 – напруженості магнітного поля;
– напруженості магнітного поля; 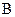 – магнітної індукції;
– магнітної індукції; 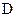 – електричного зміщення.
– електричного зміщення.
Сила дії ЕМП на заряд. ЕМП виявляється по його силовій дії на заряджені частинки. Ця сила (лоренцова) – суперпозиція сил, які створюються електричною і магнітною складовими поля:
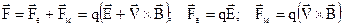 , (1.9)
, (1.9)
де  – сила дії на заряд електричного поля;
– сила дії на заряд електричного поля;
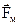 – сила дії на заряд магнітного поля;
– сила дії на заряд магнітного поля;
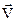 – вектор швидкості руху заряду.
– вектор швидкості руху заряду.
Розглянемо окремо  і
і 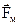 .
.
Вектори електричного поля. Через те, що 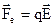 , вектор напруженості електричного поля дорівнює границі відношення сил дії поля на нерухомий точковий заряд до величині цього заряду при
, вектор напруженості електричного поля дорівнює границі відношення сил дії поля на нерухомий точковий заряд до величині цього заряду при  :
:
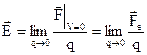 . (1.10)
. (1.10)
Розмірність вектора  можна визначити з (1.9):
можна визначити з (1.9): 
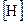 =
= 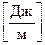 ;
; 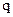
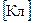 =
=  ;
; 
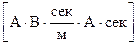 =
= 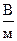 .
.
Якщо 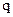 – позитивний, то напрямок
– позитивний, то напрямок  і
і  співпадає,
співпадає,  не залежить від швидкості заряду.
не залежить від швидкості заряду.
Матеріальні рівняння електричного поля. Сила взаємодії зарядів, а відповідно, напруженість електричного поля в різних середовищах різні. Фізика цього процесу: під дією електричного поля речовина поляризується. В результаті з’являється додаткове електричне поле, яке накладається на первинне. При цьому сумарне поле відрізняється від поля у вакуумі.
Введемо поняття електричного диполя і розглянемо його характеристики. Електричний диполь – це система з двох жорстко зв’язаних точкових різнойменних електричних зарядів 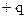 і
і  рівних по величині і рознесених на досить малу відстань
рівних по величині і рознесених на досить малу відстань  (плече диполя) в порівнянні з відстанню від диполя до точки спостереження. Диполі, як правило, характеризуються дипольним моментом
(плече диполя) в порівнянні з відстанню від диполя до точки спостереження. Диполі, як правило, характеризуються дипольним моментом 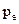 . Дипольний момент – це вектор, який визначається добутком заряду на плече диполя;
. Дипольний момент – це вектор, який визначається добутком заряду на плече диполя; 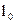 напрямлений від
напрямлений від  до
до 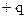 (рис. 1.3)
(рис. 1.3)
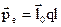 . (1.11)
. (1.11)
Сумарний дипольний момент об’єму 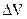 речовини дорівнює геометричній сумі дипольних моментів
речовини дорівнює геометричній сумі дипольних моментів 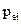 молекул в цьому об’ємі:
молекул в цьому об’ємі:
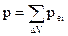 .
.
Зовнішнє електричне поле діє з силою на диполь, прагнучи повернути його в напрямку поля  . При цьому сила
. При цьому сила 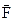 дорівнює:
дорівнює:
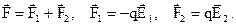
Для однорідного поля (яке не залежить від напрямку) 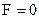 . Якщо кут
. Якщо кут 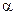 між
між  і
і  відрізняється від нуля, то до диполя прикладений обертаючий момент
відрізняється від нуля, то до диполя прикладений обертаючий момент 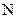
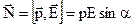 . (1.12)
. (1.12)
Для характеристики поляризації вводять вектор поляризованості 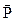
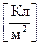 , який визначається як границя відношення сумарного дипольного моменту речовини в об’ємі
, який визначається як границя відношення сумарного дипольного моменту речовини в об’ємі 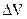 до величини цього об’єму при
до величини цього об’єму при 
 . (1.13)
. (1.13)
 не можна розглядати в строго математичному змісті: при будь-якому зменшені
не можна розглядати в строго математичному змісті: при будь-якому зменшені 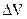 його треба вважати достатньо великим в порівняні з об’ємом молекули. Аналогічне припущення необхідно віднести до
його треба вважати достатньо великим в порівняні з об’ємом молекули. Аналогічне припущення необхідно віднести до 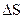 і до
і до 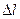 . Далі будемо вважати, що умова виконується.
. Далі будемо вважати, що умова виконується.
Якщо зовнішнє поле невелике, то величину вектора поляризованості 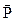 можна вважати пропорційною
можна вважати пропорційною  – напруженості електричного поля
– напруженості електричного поля
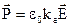 , (1.14)
, (1.14)
де 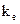 – безрозмірний параметр, який характеризує середовище і називається діелектричною сприйнятливістю середовища, а сталий коефіцієнт
– безрозмірний параметр, який характеризує середовище і називається діелектричною сприйнятливістю середовища, а сталий коефіцієнт 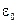
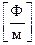 називається електричною сталою,
називається електричною сталою,
 .
.
При розгляді багатьох процесів, зручно ввести вектор 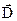
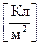 , який називається вектором електричного зміщення. Він пов’язаний з
, який називається вектором електричного зміщення. Він пов’язаний з 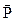 таким співвідношенням
таким співвідношенням
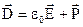 , (1.15)
, (1.15)
або з урахуванням формули (1.14) формулу (1.15) можна записати
 , (1.16)
, (1.16)
де
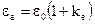 . (1.17)
. (1.17)
Параметр 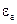 називається абсолютною діелектричною проникністю середовища. Для вакууму
називається абсолютною діелектричною проникністю середовища. Для вакууму 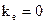 , і
, і 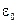 можна вважати діелектричною проникністю вакууму.
можна вважати діелектричною проникністю вакууму.
Поряд з 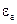 вводять поняття відносної діелектричної проникності e, яка зв’язана з eа співвідношенням
вводять поняття відносної діелектричної проникності e, яка зв’язана з eа співвідношенням
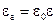 . (1.18)
. (1.18)
Зв’язок відносної діелектричної проникності і діелектричної сприйнятливості 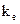 можна знайти, якщо порівняти (1.18) і (1.19):
можна знайти, якщо порівняти (1.18) і (1.19):
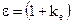 . (1.19)
. (1.19)
Треба підкреслити, що співвідношення для 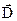 і
і 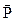 приблизні. В разі сильного поля, пропорційність між
приблизні. В разі сильного поля, пропорційність між  та
та 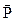 порушується, це стосується і
порушується, це стосується і 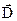 та
та 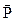 .
.
Розглянемо електричне поле, яке створюється точковим зарядом 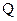 . Згідно закону Кулона сила, з якою точковий заряд
. Згідно закону Кулона сила, з якою точковий заряд 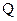 діє на точковий заряд
діє на точковий заряд 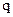 , дорівнює
, дорівнює
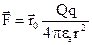 , (1.20)
, (1.20)
де 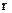 – відстань між зарядами
– відстань між зарядами 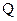 і
і 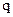 ;
;
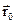 – орт вектора
– орт вектора 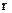 проведеного від
проведеного від 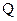 до
до 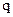 .
.
З визначення вектора  (1.10), слідує, що напруженість електричного поля, яка створюється зарядом
(1.10), слідує, що напруженість електричного поля, яка створюється зарядом 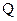 , має бути
, має бути
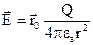 . (1.21)
. (1.21)
Для вектора 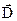 на основі рівності (1.16) отримуємо
на основі рівності (1.16) отримуємо
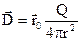 . (1.22)
. (1.22)
З (1.22) бачимо, що 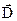 не залежить від властивостей середовища, тобто має однакове значення в різних середовищах. Це справедливо не тільки для поля точкових зарядів, але і для більш складного розподілу зарядів.
не залежить від властивостей середовища, тобто має однакове значення в різних середовищах. Це справедливо не тільки для поля точкових зарядів, але і для більш складного розподілу зарядів.
Вектори магнітного поля. Проведемо дослідження для другого доданку в (1.9), який визначається як
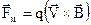 . (1.23)
. (1.23)
З (1.23) видно, що магнітна сила залежить від величини і напрямку швидкості 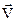 руху заряду і завжди перпендикулярна до неї. Тут
руху заряду і завжди перпендикулярна до неї. Тут 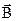 – вектор магнітної індукції, який характеризує силову дію магнітного поля; магнітна індукція вимірюється в
– вектор магнітної індукції, який характеризує силову дію магнітного поля; магнітна індукція вимірюється в 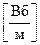 . Розмірність можна визначити з (1.23).
. Розмірність можна визначити з (1.23).
З (1.23) слідує, що магнітна індукція 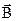 чисельно дорівнює силі, з якою магнітне поле діє на одиничний точковий позитивний заряд, який рухається з одиничною швидкістю перпендикулярно до ліній вектора
чисельно дорівнює силі, з якою магнітне поле діє на одиничний точковий позитивний заряд, який рухається з одиничною швидкістю перпендикулярно до ліній вектора 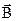 .
.
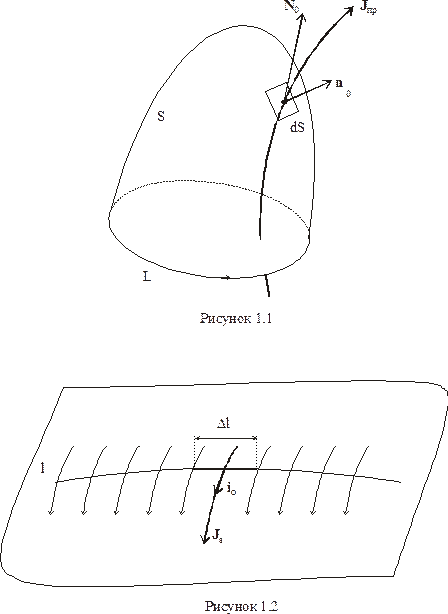
Дію однорідного магнітного поля можна виявити не тільки на окремих рухомих зарядах, але і на прямолінійному провіднику зі струмом, і на малій плоскій рамці зі струмом (рис. 1.4).
Сила взаємодії магнітного поля на провідник довжиною 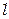 з електричним струмом визначається законом
з електричним струмом визначається законом
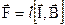 , (1.24)
, (1.24)
де 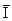 – вектор чисельно дорівнює величині струму
– вектор чисельно дорівнює величині струму 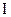 , за напрямком співпадаючим з струмом в провіднику.
, за напрямком співпадаючим з струмом в провіднику.
На рамку зі струмом буде діяти момент сил 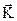 , який намагається повернути рамку так, щоб її площина була перпендикулярна вектору
, який намагається повернути рамку так, щоб її площина була перпендикулярна вектору 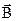 (рис. 1.4).
(рис. 1.4).
Момент сил, який діє на рамку з площею  в магнітному полі визначається виразом
в магнітному полі визначається виразом
 , (1.25)
, (1.25)
де 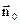 – орт нормалі до площини рамки, який утворює з напрямком струму рамки
– орт нормалі до площини рамки, який утворює з напрямком струму рамки 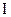 , правогвинтівну систему.
, правогвинтівну систему.
Величина
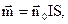 (1.26)
(1.26)
називається магнітним моментом рамки, і вимірюється в 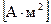 .
.
З формули (1.25) слідує, що момент сил 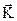 намагається повернути рамку так, щоб момент рамки співпадав з напрямком вектора
намагається повернути рамку так, щоб момент рамки співпадав з напрямком вектора 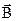 . Величина вектора
. Величина вектора 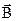 залежить від властивостей середовища. Фізично це пояснюється так як і у випадку електричного поля: під дією магнітного поля речовина намагнічується, з’являється додаткове магнітне поле, яке накладається на первинне. Сумарне поле відрізняється від поля у вакуумі.
залежить від властивостей середовища. Фізично це пояснюється так як і у випадку електричного поля: під дією магнітного поля речовина намагнічується, з’являється додаткове магнітне поле, яке накладається на первинне. Сумарне поле відрізняється від поля у вакуумі.
Намагніченість середовища характеризується вектором намагніченості 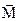
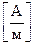 , який визначається як границя відношення сумарного магнітного моменту речовини в об’ємі
, який визначається як границя відношення сумарного магнітного моменту речовини в об’ємі 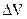 до величини цього об’єму при
до величини цього об’єму при  :
:
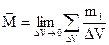 . (1.27)
. (1.27)
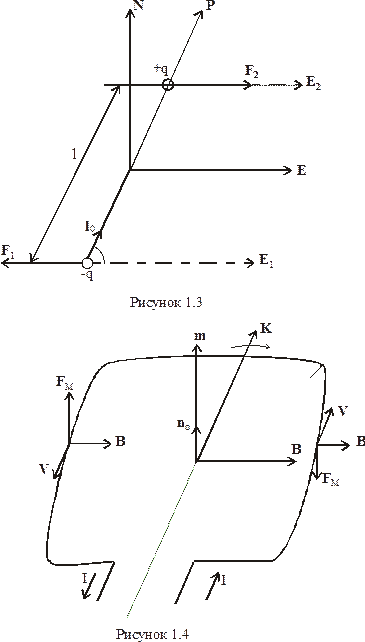
При розгляді багатьох процесів зручно ввести вектор 
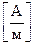 , зв’язаний з
, зв’язаний з 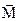 співвідношенням
співвідношенням
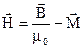 . (1.28)
. (1.28)
Це співвідношення можна переписати таким чином
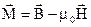 . (1.29)
. (1.29)
Величина 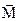 в (1.29) показує наскільки магнітна індукція даного середовища
в (1.29) показує наскільки магнітна індукція даного середовища 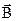 відрізняється від індукції у вакуумі. Цей вираз відрізняється від традиційного визначення вектора намагніченості з (1.28) згідно з яким
відрізняється від індукції у вакуумі. Цей вираз відрізняється від традиційного визначення вектора намагніченості з (1.28) згідно з яким
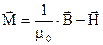 . (1.30)
. (1.30)
У вираз для  входить величина
входить величина  – стала величина, яка називається магнітною сталою:
– стала величина, яка називається магнітною сталою: 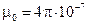
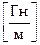 .
.
Вектор  прийнято називати напруженістю магнітного поля. Властивості
прийнято називати напруженістю магнітного поля. Властивості  : при однакових джерелах магнітного поля значення цього вектора не залежить від середовища.
: при однакових джерелах магнітного поля значення цього вектора не залежить від середовища.
В силу лінійності рівняння (1.28) можна також вважати пропорційними вектори 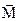 і
і 
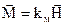 . (1.31)
. (1.31)
Коефіцієнт 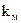 називають магнітною сприйнятливістю середовища.
називають магнітною сприйнятливістю середовища.
У діамагнітних середовищах 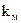 від’ємна, у парамагнітних і феромагнітних – позитивна. У діамагнітних матеріалів
від’ємна, у парамагнітних і феромагнітних – позитивна. У діамагнітних матеріалів 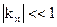 , у феромагнітних
, у феромагнітних 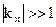 . Підставляючи (1.30) в (1.28) отримуємо
. Підставляючи (1.30) в (1.28) отримуємо
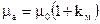 , (1.32)
, (1.32)
де 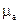 – абсолютна магнітна проникність.
– абсолютна магнітна проникність.
Магнітну сталу  можна розглядати як магнітну проникність вакууму при
можна розглядати як магнітну проникність вакууму при 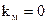 . Вводиться поняття відносної магнітної проникності, яка зв’язана з
. Вводиться поняття відносної магнітної проникності, яка зв’язана з 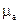 співвідношенням
співвідношенням
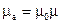 . (1.33)
. (1.33)
Якщо порівняти (1.33) і (1.32), то можна знайти зв’язок 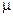 і
і 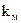
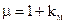 . (1.34)
. (1.34)
При слабких полях зв’язок між  і
і 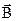 вірний, при цьому для діамагнетиків і парамагнетиків
вірний, при цьому для діамагнетиків і парамагнетиків 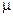 , як правило, скалярна величина, а для феромагнетиків вона тензор
, як правило, скалярна величина, а для феромагнетиків вона тензор 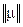 . Рівняння для векторів
. Рівняння для векторів  і
і 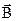 наближені, через те, що
наближені, через те, що 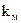 істотно залежить від величини магнітного поля. Крім того феромагнітні матеріали мають явище магнітного гістерезису.
істотно залежить від величини магнітного поля. Крім того феромагнітні матеріали мають явище магнітного гістерезису.


 – напруженості електричного поля;
– напруженості електричного поля; 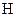 – напруженості магнітного поля;
– напруженості магнітного поля; 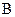 – магнітної індукції;
– магнітної індукції; 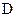 – електричного зміщення.
– електричного зміщення.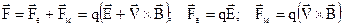 , (1.9)
, (1.9) – сила дії на заряд електричного поля;
– сила дії на заряд електричного поля;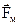 – сила дії на заряд магнітного поля;
– сила дії на заряд магнітного поля;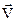 – вектор швидкості руху заряду.
– вектор швидкості руху заряду.
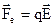 , вектор напруженості електричного поля дорівнює границі відношення сил дії поля на нерухомий точковий заряд до величині цього заряду при
, вектор напруженості електричного поля дорівнює границі відношення сил дії поля на нерухомий точковий заряд до величині цього заряду при  :
: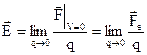 . (1.10)
. (1.10) можна визначити з (1.9):
можна визначити з (1.9): 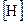 =
= 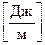 ;
; 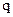
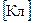 =
=  ;
; 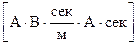 =
= 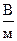 .
.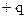 і
і  рівних по величині і рознесених на досить малу відстань
рівних по величині і рознесених на досить малу відстань  (плече диполя) в порівнянні з відстанню від диполя до точки спостереження. Диполі, як правило, характеризуються дипольним моментом
(плече диполя) в порівнянні з відстанню від диполя до точки спостереження. Диполі, як правило, характеризуються дипольним моментом 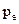 . Дипольний момент – це вектор, який визначається добутком заряду на плече диполя;
. Дипольний момент – це вектор, який визначається добутком заряду на плече диполя; 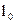 напрямлений від
напрямлений від 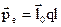 . (1.11)
. (1.11)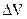 речовини дорівнює геометричній сумі дипольних моментів
речовини дорівнює геометричній сумі дипольних моментів 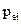 молекул в цьому об’ємі:
молекул в цьому об’ємі: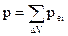 .
.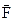 дорівнює:
дорівнює: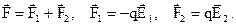
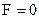 . Якщо кут
. Якщо кут 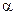 між
між  відрізняється від нуля, то до диполя прикладений обертаючий момент
відрізняється від нуля, то до диполя прикладений обертаючий момент 
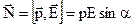 . (1.12)
. (1.12)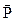
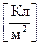 , який визначається як границя відношення сумарного дипольного моменту речовини в об’ємі
, який визначається як границя відношення сумарного дипольного моменту речовини в об’ємі 
 . (1.13)
. (1.13)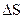 і до
і до 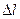 . Далі будемо вважати, що умова виконується.
. Далі будемо вважати, що умова виконується.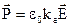 , (1.14)
, (1.14)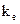 – безрозмірний параметр, який характеризує середовище і називається діелектричною сприйнятливістю середовища, а сталий коефіцієнт
– безрозмірний параметр, який характеризує середовище і називається діелектричною сприйнятливістю середовища, а сталий коефіцієнт 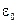
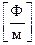 називається електричною сталою,
називається електричною сталою, .
.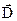
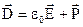 , (1.15)
, (1.15) , (1.16)
, (1.16)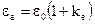 . (1.17)
. (1.17)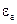 називається абсолютною діелектричною проникністю середовища. Для вакууму
називається абсолютною діелектричною проникністю середовища. Для вакууму 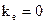 , і
, і 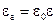 . (1.18)
. (1.18)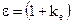 . (1.19)
. (1.19)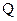 . Згідно закону Кулона сила, з якою точковий заряд
. Згідно закону Кулона сила, з якою точковий заряд 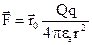 , (1.20)
, (1.20)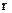 – відстань між зарядами
– відстань між зарядами 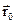 – орт вектора
– орт вектора  (1.10), слідує, що напруженість електричного поля, яка створюється зарядом
(1.10), слідує, що напруженість електричного поля, яка створюється зарядом 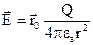 . (1.21)
. (1.21)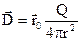 . (1.22)
. (1.22)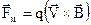 . (1.23)
. (1.23)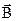 – вектор магнітної індукції, який характеризує силову дію магнітного поля; магнітна індукція вимірюється в
– вектор магнітної індукції, який характеризує силову дію магнітного поля; магнітна індукція вимірюється в 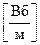 . Розмірність можна визначити з (1.23).
. Розмірність можна визначити з (1.23).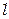 з електричним струмом визначається законом
з електричним струмом визначається законом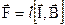 , (1.24)
, (1.24)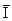 – вектор чисельно дорівнює величині струму
– вектор чисельно дорівнює величині струму 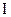 , за напрямком співпадаючим з струмом в провіднику.
, за напрямком співпадаючим з струмом в провіднику.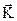 , який намагається повернути рамку так, щоб її площина була перпендикулярна вектору
, який намагається повернути рамку так, щоб її площина була перпендикулярна вектору  в магнітному полі визначається виразом
в магнітному полі визначається виразом , (1.25)
, (1.25)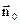 – орт нормалі до площини рамки, який утворює з напрямком струму рамки
– орт нормалі до площини рамки, який утворює з напрямком струму рамки 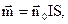 (1.26)
(1.26)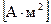 .
.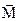
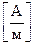 , який визначається як границя відношення сумарного магнітного моменту речовини в об’ємі
, який визначається як границя відношення сумарного магнітного моменту речовини в об’ємі 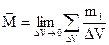 . (1.27)
. (1.27)

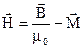 . (1.28)
. (1.28)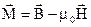 . (1.29)
. (1.29)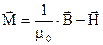 . (1.30)
. (1.30) – стала величина, яка називається магнітною сталою:
– стала величина, яка називається магнітною сталою: 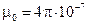
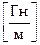 .
.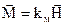 . (1.31)
. (1.31)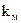 називають магнітною сприйнятливістю середовища.
називають магнітною сприйнятливістю середовища.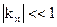 , у феромагнітних
, у феромагнітних 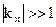 . Підставляючи (1.30) в (1.28) отримуємо
. Підставляючи (1.30) в (1.28) отримуємо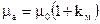 , (1.32)
, (1.32)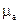 – абсолютна магнітна проникність.
– абсолютна магнітна проникність.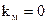 . Вводиться поняття відносної магнітної проникності, яка зв’язана з
. Вводиться поняття відносної магнітної проникності, яка зв’язана з 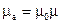 . (1.33)
. (1.33)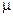 і
і 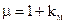 . (1.34)
. (1.34)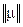 . Рівняння для векторів
. Рівняння для векторів