Властивості середовища характеризуються параметрами  . Параметр
. Параметр 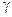 носить назву питомої провідності середовища
носить назву питомої провідності середовища  . Розрізняють такі середовища:
. Розрізняють такі середовища:
– лінійні, в яких параметри 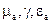 не залежать від величини електричного і магнітного поля;
не залежать від величини електричного і магнітного поля;
– нелінійні, в яких параметри 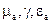 або хоча б один із них, залежить від величини електричного і магнітного поля.
або хоча б один із них, залежить від величини електричного і магнітного поля.
Всі реальні середовища нелінійні. В подальшому при слабких полях середовище, яке розглядається, буде вважатися лінійним.
Лінійні середовища поділяються на однорідні, неоднорідні, ізотропні, анізотропні:
однорідні – середовища у яких параметри середовища не залежать від координат;
неоднорідні – хоча б один параметр являється функцією координат;
ізотропні – якщо властивості середовища однакові у всіх напрямках. В цих середовищах вектори 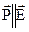 ,
, 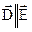 , а також
, а також 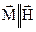 ,
, 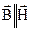 . Параметри
. Параметри  – скалярні величини;
– скалярні величини;
анізотропні – якщо властивості різні в різних напрямках. В таких середовищах перераховані вектори електромагнітного поля (ЕМП) можуть бути не паралельними, якщо  , або хоча б один з них, являється тензором.
, або хоча б один з них, являється тензором.
“Тензор” походить від латинського “tensus” (напружений). Це математичний об’єкт, який узагальнює скалярні і векторні величини, матриці і т.д. В кожній системі координат тензор задається сукупністю чисел, взятих в певному порядку. В тривимірному просторі – це сукупність дев’яти величин.
В кристалічному діелектрику 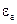 являється тензором. В загальному випадку він записується у вигляді матриці:
являється тензором. В загальному випадку він записується у вигляді матриці:
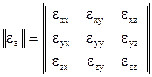 . (1.35)
. (1.35)
При цьому форма рівнянь (1.16) залишається тією ж:
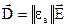 . (1.36)
. (1.36)
В декартовій системі координат кожна проекція вектора 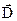 запишеться у вигляді лінійної комбінації всіх трьох проекцій вектора
запишеться у вигляді лінійної комбінації всіх трьох проекцій вектора  :
:
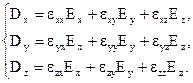 (1.37)
(1.37)
Непаралельність векторів електричного поля 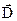 і
і  (а також
(а також  і
і 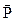 ) в анізотропному середовищі пояснюється наявністю кута (відмінним від 0 і
) в анізотропному середовищі пояснюється наявністю кута (відмінним від 0 і  ) між вторинним полем в результаті поляризації і первинним електричним полем.
) між вторинним полем в результаті поляризації і первинним електричним полем.
У феромагнітних середовищах тензором буде магнітна проникність 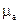 . Запис для
. Запис для 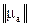 аналогічний (1.35). При цьому форма рівняння (1.32) зберігається:
аналогічний (1.35). При цьому форма рівняння (1.32) зберігається:
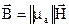 . (1.38)
. (1.38)
Розписуючи (1.38) в проекціях на осі декартової системи координат 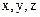 , приходимо до формул, аналогічних (1.37).
, приходимо до формул, аналогічних (1.37).
В ряді випадків тензором може бути і питома провідність 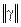 .
.


 . Параметр
. Параметр 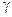 носить назву питомої провідності середовища
носить назву питомої провідності середовища  . Розрізняють такі середовища:
. Розрізняють такі середовища: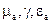 не залежать від величини електричного і магнітного поля;
не залежать від величини електричного і магнітного поля;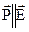 ,
, 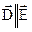 , а також
, а також 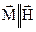 ,
, 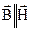 . Параметри
. Параметри 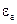 являється тензором. В загальному випадку він записується у вигляді матриці:
являється тензором. В загальному випадку він записується у вигляді матриці: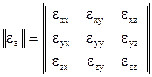 . (1.35)
. (1.35)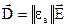 . (1.36)
. (1.36)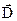 запишеться у вигляді лінійної комбінації всіх трьох проекцій вектора
запишеться у вигляді лінійної комбінації всіх трьох проекцій вектора  :
: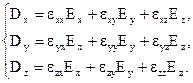 (1.37)
(1.37)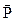 ) в анізотропному середовищі пояснюється наявністю кута (відмінним від 0 і
) в анізотропному середовищі пояснюється наявністю кута (відмінним від 0 і  ) між вторинним полем в результаті поляризації і первинним електричним полем.
) між вторинним полем в результаті поляризації і первинним електричним полем.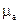 . Запис для
. Запис для 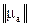 аналогічний (1.35). При цьому форма рівняння (1.32) зберігається:
аналогічний (1.35). При цьому форма рівняння (1.32) зберігається: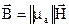 . (1.38)
. (1.38)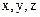 , приходимо до формул, аналогічних (1.37).
, приходимо до формул, аналогічних (1.37).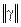 .
.