Електричний заряд – одне із властивостей елементарних частинок речовини. Розрізняють два види зарядів – позитивні та негативні. Експериментально виявлена дискретна структура зарядів. Величина будь-яких зарядів, які зустрічаються в природі, кратна заряду електрона 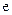 , який дорівнює приблизно
, який дорівнює приблизно 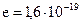 Кл. Електричні заряди обумовлюють електричні і магнітні явища.
Кл. Електричні заряди обумовлюють електричні і магнітні явища.
Величина електричного заряду вимірюється в кулонах (Кл) і позначається символом 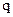 . В ідеалізованому випадку електричний заряд вважають точковим, тобто нехтують його розмірами.
. В ідеалізованому випадку електричний заряд вважають точковим, тобто нехтують його розмірами.
Якщо він розподілений в просторі, то його називають об’ємним і характеризують об’ємною густиною, яка має розмірність 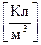
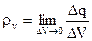 , (1.3)
, (1.3)
де 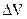 – елемент об’єму.
– елемент об’єму.
Під об’ємним зарядом розуміють скалярну величину, яка дорівнює границі відношення об’ємного заряду до об’єму в якому він розподілений, при  . З (1.3) видно, що повний заряд, який знаходиться в деякому об’ємі, визначається таким чином:
. З (1.3) видно, що повний заряд, який знаходиться в деякому об’ємі, визначається таким чином:
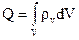 . (1.4)
. (1.4)
Q вимірюється у 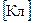 .
.
Електричний заряд може бути розподілений по поверхні у вигляді нескінченного шару і називається поверхневим зарядом і характеризується поверхневою густиною  , яка визначається
, яка визначається
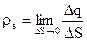 , (1.5)
, (1.5)
де 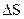 – елемент поверхні, а
– елемент поверхні, а 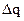 – заряд цього елемента; rs має розмірність
– заряд цього елемента; rs має розмірність 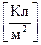 .
.
Густина електричного струму. Впорядкований рух зарядів створює електричний струм (струми провідності), які характеризуються вектором об’ємної густини струму провідності (рис. 1.1) та має розмірність 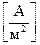 :
:
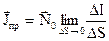 , (1.6)
, (1.6)
де 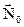 – одиничний вектор, який вказує напрям струму;
– одиничний вектор, який вказує напрям струму;
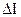 – струм, який протікає через площинку
– струм, який протікає через площинку 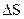 , перпендикулярно
, перпендикулярно 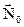 .
.
Інтегруючи 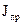 по поверхні
по поверхні  , отримуємо результуючий струм провідності
, отримуємо результуючий струм провідності
 , (1.7)
, (1.7)
де 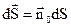 ;
;
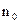 – нормаль в даній точці поверхні
– нормаль в даній точці поверхні  .
.
Вектор 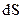 напрямлений по
напрямлений по 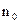 і дорівнює по величині
і дорівнює по величині 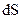 (рис. 1.1).
(рис. 1.1).
Особливий інтерес має випадок, коли струми розподілені вздовж поверхні у вигляді нескінченного шару. Такі струми називаються поверхневими (рис. 1.2). Густина поверхневих струмів визначається співвідношенням:
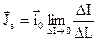 , (1.8)
, (1.8)
де 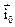 – одиничний вектор, який показує напрямок руху позитивних зарядів в даній точці;
– одиничний вектор, який показує напрямок руху позитивних зарядів в даній точці;
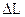 – відрізок лінії перпендикулярний вектору
– відрізок лінії перпендикулярний вектору 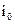 ;
;
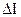 – величина струму, який протікає через відрізок
– величина струму, який протікає через відрізок 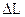 ;
;
розмірність 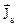 -
- 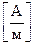 .
.


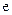 , який дорівнює приблизно
, який дорівнює приблизно 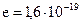 Кл. Електричні заряди обумовлюють електричні і магнітні явища.
Кл. Електричні заряди обумовлюють електричні і магнітні явища.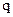 . В ідеалізованому випадку електричний заряд вважають точковим, тобто нехтують його розмірами.
. В ідеалізованому випадку електричний заряд вважають точковим, тобто нехтують його розмірами.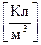
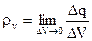 , (1.3)
, (1.3)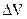 – елемент об’єму.
– елемент об’єму. . З (1.3) видно, що повний заряд, який знаходиться в деякому об’ємі, визначається таким чином:
. З (1.3) видно, що повний заряд, який знаходиться в деякому об’ємі, визначається таким чином: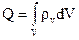 . (1.4)
. (1.4)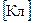 .
. , яка визначається
, яка визначається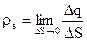 , (1.5)
, (1.5)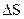 – елемент поверхні, а
– елемент поверхні, а 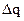 – заряд цього елемента; rs має розмірність
– заряд цього елемента; rs має розмірність 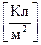 .
.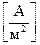 :
: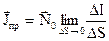 , (1.6)
, (1.6)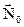 – одиничний вектор, який вказує напрям струму;
– одиничний вектор, який вказує напрям струму;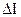 – струм, який протікає через площинку
– струм, який протікає через площинку 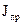 по поверхні
по поверхні  , отримуємо результуючий струм провідності
, отримуємо результуючий струм провідності , (1.7)
, (1.7)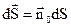 ;
;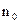 – нормаль в даній точці поверхні
– нормаль в даній точці поверхні 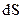 напрямлений по
напрямлений по 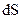 (рис. 1.1).
(рис. 1.1).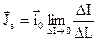 , (1.8)
, (1.8)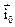 – одиничний вектор, який показує напрямок руху позитивних зарядів в даній точці;
– одиничний вектор, який показує напрямок руху позитивних зарядів в даній точці;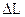 – відрізок лінії перпендикулярний вектору
– відрізок лінії перпендикулярний вектору 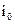 ;
;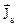 -
- 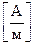 .
.