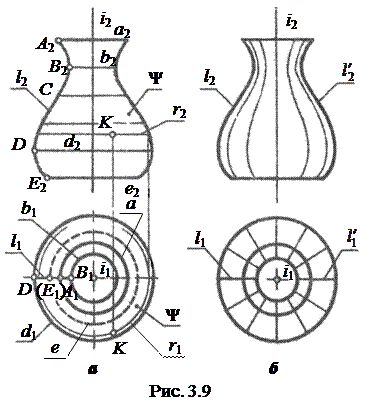
Поверхнею обертання називається поверхня, яка утворена обертанням твірної лінії (прямої або кривої) навколо нерухомої прямої, яка називається віссю поверхні обертання.
Площина, яка проходе через вісь поверхні обертання називається меридіональною площиною, а лінія її перетину з поверхнею обертання називається меридіаном. Якщо січна площина паралельна П2, то такий меридіан називається головним.
При обертання твірної кожна її точка опише коло з центром на осі обертання. Площини цих кіл перпендикулярні до осі і взаємно паралельні. Ці кола називаються паралелями.
Паралель найменшого радіуса називається горлом поверхні, а найбільшого радіуса – екватором. Верхня та нижня паралелі називаються лініями відсіку (або відрізу) поверхні.
Меридіани та паралелі утворюють каркас поверхні.
Поверхні обертання другого порядку
Порядок поверхні визначається кількістю точок перетину цієї поверхні з прямою лінією, або степенем алгебраїчного рівняння, яке описує цю поверхню.
Розглянемо поверхні, які утворені обертанням кривих другого порядку навколо осі. Безпосередньо криві в цьому випадку є й твірними, й меридіанами поверхні.
При обертанні кола a навколо його осі (діаметра) утворюється поверхня сфери Φ (рис. 3.10). Точку A побудовано з використанням паралелі сфери. Обидві проекції цієї точки видимі.
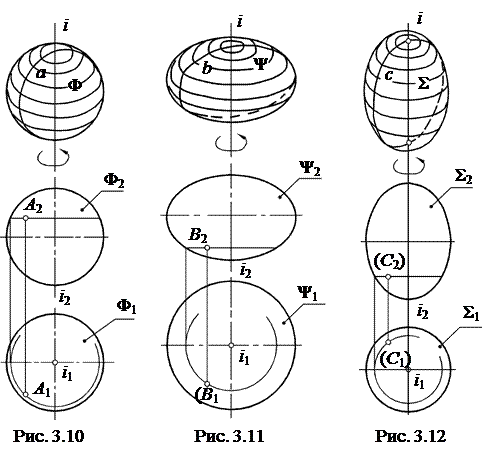
При обертанні еліпса b навколо його малої осі утворюється поверхня стислого еліпсоїда або сфероїда Ψ (рис. 3.11). Проекції точки B побудовані з використанням паралелі еліпсоїда. Оскільки B2 знаходиться нижче горизонтальної осі проекції поверхні на П2, то її горизонтальна проекція невидима.
При обертанні еліпса с навколо його великої осі утворюється поверхня витягнутого еліпсоїда Σ (рис. 3.12). Проекції точки С на обох площинах проекцій невидимі.
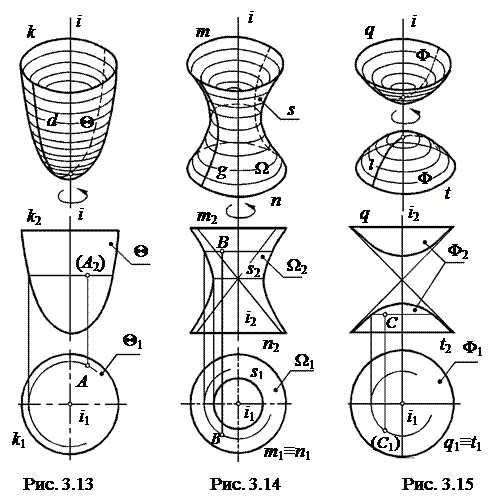
При обертанні параболи d навколо її осі i утворюється поверхня параболоїда обертання Θ (рис. 3.13).
При обертанні гіперболи g навколо її уявної осі i утворюється поверхня однопорожнинного гіперболоїда обертання Ω (рис. 3.14). Якщо ж гіперболу l обертати навколо її дійсної осі i, то буде утворена поверхня двохпорожнинного гіперболоїда обертання Φ (рис. 3.15), яка складається з двох окремих порожнин.
