Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
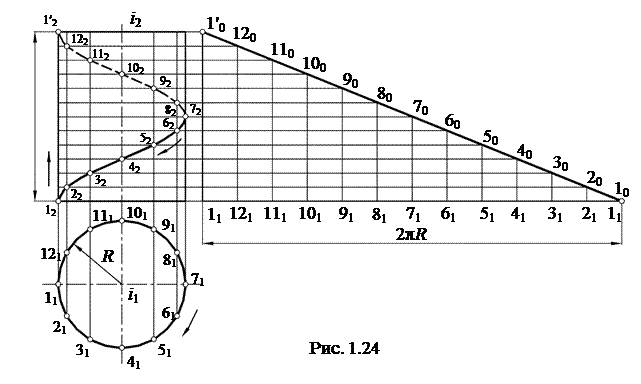
Просторові криві лініїДата додавання: 2014-10-07; переглядів: 1747.
|
Онлайн система числення Калькулятор онлайн звичайний Науковий калькулятор онлайн
| |||||||||||||||||||