Спосіб заміни площин проекцій є протилежним до способів обертання та плоско-паралельного переміщення. Там змінювалось положення геометричного образу у просторі, а площини проекцій залишалися на місці. Зараз розглянемо спосіб, коли геометричний образ залишається на місці.
Геометричний образ свого положення у просторі не змінює. При виборі положення нової площини проекцій керуються тим, що по відношенню до нової площини образ, що проекціюється, має зайняти окреме положення, яке забезпечує здобуття проекцій найбільш зручних для розв’язання задачі.
Нові площини проекцій будемо позначати, як П4, П5, П6 і так далі. Можна сказати, що "старі" площини проекцій П1 і П2 замінюються новими площинами П4, П5 тощо. Звідси випливає назва способу перетворення – заміна площин проекцій.
В деяких випадках достатньо замінити тільки одну площину проекцій П1 на П4 або П2 на П4. Якщо така заміна не забезпечує бажаного вигляду нової проекції геометричного образу, то виконують заміну двох площин.
При заміні площин проекцій необхідно дотримуватись таких умов:
1) площини проекцій замінюються не одночасно, а послідовно;
2) кожна нова площина проекцій має бути перпендикулярною до тієї площини, яка залишається та утворює з нею нову систему площин проекцій.
Розглянемо суть способу заміни площин проекцій на прикладі точок, прямих і площин та розв’яжемо чотири основні задачі на перетворення.
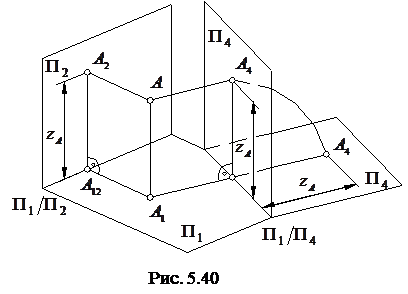 Подивимося, які зміни відбуваються з проекціями точки при переході від однієї системи площин проекцій до іншої. На рис. 5.40 показано точку А, що знаходиться в системі площин проекцій
Подивимося, які зміни відбуваються з проекціями точки при переході від однієї системи площин проекцій до іншої. На рис. 5.40 показано точку А, що знаходиться в системі площин проекцій  . Замінимо одну з цих площин, наприклад П2, іншою, також вертикальною площиною П4 і побудуємо проекцію точки А на цю площину. Оскільки горизонтальна площина проекцій П1 є спільною для "старої" та "нової" систем, то координата z точки А залишається незмінною. Отже, відстань від нової проекції
. Замінимо одну з цих площин, наприклад П2, іншою, також вертикальною площиною П4 і побудуємо проекцію точки А на цю площину. Оскільки горизонтальна площина проекцій П1 є спільною для "старої" та "нової" систем, то координата z точки А залишається незмінною. Отже, відстань від нової проекції  до нової осі
до нової осі  дорівнює відстані від проекції, що замінюється, до осі
дорівнює відстані від проекції, що замінюється, до осі 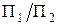 . При цьому проекцію
. При цьому проекцію  визначено як основу перпендикуляра, проведеного із точки А на П4. Горизонтальна проекція
визначено як основу перпендикуляра, проведеного із точки А на П4. Горизонтальна проекція 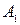 залишається тією ж самою, але координата у точки А тепер інша. Вона визначається відстанню від точки А до площини П4, яка на комплексному кресленні дорівнює відстані від проекції
залишається тією ж самою, але координата у точки А тепер інша. Вона визначається відстанню від точки А до площини П4, яка на комплексному кресленні дорівнює відстані від проекції 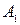 до осі
до осі 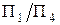 . Відзначимо, що ця вісь на кресленні вибрана довільно.
. Відзначимо, що ця вісь на кресленні вибрана довільно.
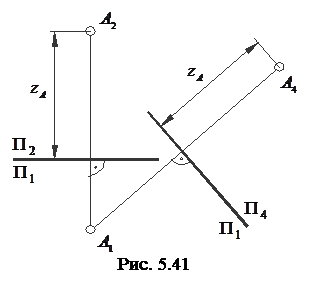 Для побудови комплексного креслення площина П4 обертанням навколо осі
Для побудови комплексного креслення площина П4 обертанням навколо осі 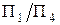 суміщається з площиною П1. Суміститься з П1 й нова проекція
суміщається з площиною П1. Суміститься з П1 й нова проекція  точки А, яка виявиться на спільному перпендикулярі до нової осі
точки А, яка виявиться на спільному перпендикулярі до нової осі 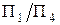 , проведеному з горизонтальної проекції
, проведеному з горизонтальної проекції 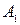 точки А (рис. 5.41).
точки А (рис. 5.41).
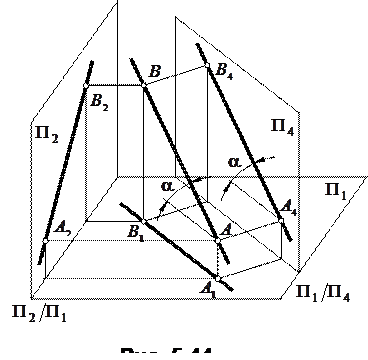 Розв’язання чотирьох основних задач способом заміни площин проекцій
Розв’язання чотирьох основних задач способом заміни площин проекцій
Перетворення прямої загального положення в пряму рівня (задача 1). Нехай у системі площин  /
/  задано відрізок АВ прямої загального положення (рис. 5.44). Для того, щоб у новій системі площин ця пряма зайняла положення прямої рівня, необхідно нову площину проекцій
задано відрізок АВ прямої загального положення (рис. 5.44). Для того, щоб у новій системі площин ця пряма зайняла положення прямої рівня, необхідно нову площину проекцій  розташувати паралельно відрізку АВ і перпендикулярно до площини проекцій
розташувати паралельно відрізку АВ і перпендикулярно до площини проекцій  . Утворюється нова система взаємно перпендикулярних площин
. Утворюється нова система взаємно перпендикулярних площин  ,
,  , вісь
, вісь 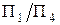 якої паралельна проекції
якої паралельна проекції 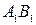 відрізка АВ. Спроекціювавши АВ на площину
відрізка АВ. Спроекціювавши АВ на площину 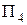 , отримаємо його проекцію
, отримаємо його проекцію 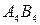 . Для здобуття нового плоского комплексного креслення площину
. Для здобуття нового плоского комплексного креслення площину 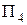 обертанням навколо осі
обертанням навколо осі 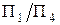 суміщаємо з площиною
суміщаємо з площиною  .
.
У системі площин проекцій  ,
, 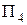 пряма АВ є прямою рівня, її проекція на
пряма АВ є прямою рівня, її проекція на 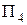 дорівнює натуральній величині відрізка АВ, а кут a між проекцією
дорівнює натуральній величині відрізка АВ, а кут a між проекцією 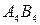 та новою віссю
та новою віссю 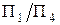 є кутом нахилу відрізка АВ до площини
є кутом нахилу відрізка АВ до площини  .
.
Переходимо до комплексного креслення (рис. 5.45). На цьому кресленні в системі площин  ,
, 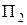 маємо відрізок АВ прямої загального положення. собою горизонтальну площину проекцій
маємо відрізок АВ прямої загального положення. собою горизонтальну площину проекцій  . На цьому кресленні в системі площин
. На цьому кресленні в системі площин  ,
, 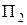 маємо відрізок АВ прямої загального положення. собою горизонтальну площину проекцій
маємо відрізок АВ прямої загального положення. собою горизонтальну площину проекцій  .
.
Перехід до нової системи площин реалізується у три кроки:
1. Будується нова вісь проекцій у відповідності до умов задачі. В нашому випадку нова вісь проекцій 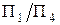 паралельна горизонтальній проекції
паралельна горизонтальній проекції 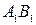 відрізка АВ. Відстань від нової осі проекцій до проекції
відрізка АВ. Відстань від нової осі проекцій до проекції 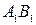 довільна.
довільна.
2. Проводяться нові лінії сполучення перпендикулярно до нової осі проекцій. Ці лінії починаються від тих проекцій точок, які переходять до нового креслення. На рис. 5.45 лінії сполучення йдуть від кінців 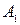 ,
, 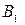 горизонтальної проекції відрізка до нових проекцій, перпендикулярно до нової осі.
горизонтальної проекції відрізка до нових проекцій, перпендикулярно до нової осі.
3. На нових лініях сполучення від нової осі відкладають відстані, рівні відстаням від "старих" проекцій точок до старої осі (у нашому випадку це координати z точок А і В, тобто віддалення проекцій 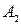 і
і 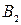 від осі
від осі 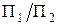 ).
).
Якщо треба знайти кут b нахилу відрізка АВ до площини 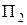 , то площину проекцій
, то площину проекцій  замінюють новою площиною проекцій
замінюють новою площиною проекцій 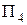 , паралельною відрізку АВ і перпендикулярною до площини проекцій
, паралельною відрізку АВ і перпендикулярною до площини проекцій 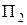
Перетворення прямої рівня в проекціювальну пряму (задача 2). Цю задачу будемо розв’язувати, як продовження першої задачі.
Розглянемо комплексне креслення (рис. 5.48). Для зручності комплексне креслення в системі площин  ,
, 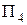 , повернуто таким чином, щоб положення осі проекцій
, повернуто таким чином, щоб положення осі проекцій 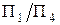 відповідало наочному зображенню рис. 5.47.
відповідало наочному зображенню рис. 5.47.
Перехід до нової системи площин на комплексному кресленні реалізується в тому ж порядку, який використовувався при розв’язанні попередньої задачі (задачі 1):
1. Будуємо вісь проекцій 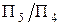 перпендикулярно до проекції
перпендикулярно до проекції 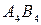 , що випливає з умови задачі, пов’язаної з перетворенням прямої рівня у пряму проекціювальну.
, що випливає з умови задачі, пов’язаної з перетворенням прямої рівня у пряму проекціювальну.
2. Через проекції 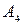 і
і 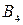 , що переходять із старого у нове комплексне креслення, проводимо нові лінії сполучення, перпендикулярно до нової осі
, що переходять із старого у нове комплексне креслення, проводимо нові лінії сполучення, перпендикулярно до нової осі 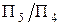 (зрозуміло, що у нашому випадку ці лінії збігаються).
(зрозуміло, що у нашому випадку ці лінії збігаються).
3. На нових лініях сполучення від нової осі відкладаємо відрізки, що відповідають відстаням від горизонтальних проекцій 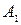 і
і 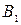 точок до старої осі
точок до старої осі 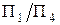 . Отримуємо нову, додаткову проекцію
. Отримуємо нову, додаткову проекцію 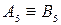 відрізка АВ.
відрізка АВ.
Таким чином, маємо нове комплексне креслення, яке складається із старої проекції 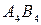 та нової, додаткової проекції
та нової, додаткової проекції 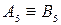 . На цьому новому кресленні пряма рівня АВ є проекціювальною прямою.
. На цьому новому кресленні пряма рівня АВ є проекціювальною прямою.
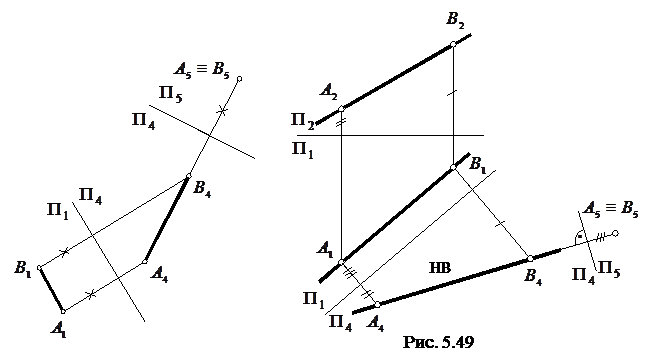
Нагадаємо, що нові осі проекцій будують на довільних відстанях від тих проекцій геометричних образів, які переходять до нового креслення. Ці відстані визначаються тільки зручністю розв’язання конкретної задачі та наявністю вільного місця на аркуші паперу.
Для перетворення прямої загального положення у проекціювальну пряму необхідно послідовно розв’язати першу та другу задачі на одному комплексному кресленні (рис.5.49). Дійсно, перетворення однієї із проекцій деякої прямої загального положення у точку вимагає подвійної заміни площин проекцій, оскільки в системі площин  ,
, 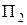 площина, перпендикулярна до цієї прямої, не буде ортогональною ні до
площина, перпендикулярна до цієї прямої, не буде ортогональною ні до  , ні до
, ні до  .
.
Перетворення площини загального положення в площину проекціювальну(задача 3). Нехай площина загального положення задана трикутним відсіком АВС (рис. 5.50). Для розв’язання цієї задачі нову площину проекцій розташовують перпендикулярно до відсіку АВС і однієї з площин проекцій. А це свідчить про те, що нова площина проекцій є перпендикулярною до лінії перетину заданої площини з однією з площин проекцій. Саму лінію не будують, оскільки її напрям визначають за допомогою головної лінії площини (горизонталі чи фронталі). Тому у заданій площині загального положення перш за все проводять одну із таких ліній, наприклад, горизонталь А1. Ця горизонталь необхідна для орієнтування нової площини проекцій  .
.
 Розташувавши
Розташувавши 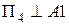 , забезпечуємо виконання одразу двох умов: нова площина
, забезпечуємо виконання одразу двох умов: нова площина 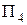 буде перпендикулярною і до
буде перпендикулярною і до  , і до площини трикутника. Нову вісь
, і до площини трикутника. Нову вісь 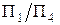 проводять під прямим кутом до
проводять під прямим кутом до  . Провівши через горизонтальні проекції вершин трикутника лінії сполучення, перпендикулярні до нової осі, відкладаємо на них від осі
. Провівши через горизонтальні проекції вершин трикутника лінії сполучення, перпендикулярні до нової осі, відкладаємо на них від осі 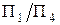 відрізки, що дорівнюють
відрізки, що дорівнюють 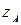 ,
,  ,
, 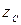 . Далі будується нова проекція
. Далі будується нова проекція 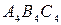 трикутника АВС, яка є прямою лінією. Додамо також, що на площину
трикутника АВС, яка є прямою лінією. Додамо також, що на площину 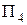 , яка перпендикулярна до трикутника і до площини проекцій
, яка перпендикулярна до трикутника і до площини проекцій  , без спотворення проекціюється кут
, без спотворення проекціюється кут 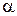 , утворений трикутним відсіком з площиною проекцій
, утворений трикутним відсіком з площиною проекцій  .
.
Перетворення проекціювальної площини в площину рівня (задача 4). Цю задачу будемо розглядати як продовження попередньої (третьої) задачі. Для зручності вісь  розташуємо горизонтально.
розташуємо горизонтально.
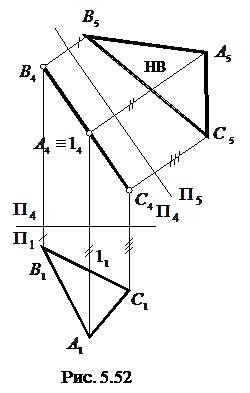 Нагадаємо, що для перетворення проекціювальної площини у площину рівня необхідно ввести нову площину проекції
Нагадаємо, що для перетворення проекціювальної площини у площину рівня необхідно ввести нову площину проекції 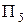 , паралельну площині трикутника. Вісь проекцій
, паралельну площині трикутника. Вісь проекцій 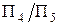 має бути паралельною "виродженій" проекції три-кутника, яка є результатом розв’язання третьої задачі.
має бути паралельною "виродженій" проекції три-кутника, яка є результатом розв’язання третьої задачі.
Спочатку паралельно проекції 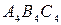 трикутника на довільній відстані від неї будують нову вісь проекцій
трикутника на довільній відстані від неї будують нову вісь проекцій 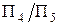 (рис. 5.52), а потім від вершин
(рис. 5.52), а потім від вершин  ,
, 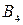 ,
, 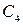 проводять нові лінії сполучення, перпендикулярні до нової осі
проводять нові лінії сполучення, перпендикулярні до нової осі 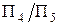 , і на них відкладають відстані, які визначають віддалення проекцій точок
, і на них відкладають відстані, які визначають віддалення проекцій точок  ,
, 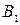 ,
, 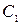 від старої осі
від старої осі 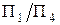 . У результаті матимемо нове комплексне креслення площини АВС, яке складається із старої проекції-прямої
. У результаті матимемо нове комплексне креслення площини АВС, яке складається із старої проекції-прямої 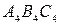 відсіку та його нової, додаткової проекції
відсіку та його нової, додаткової проекції 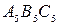 . На цьому кресленні площина АВС є площиною рівня, а проекція
. На цьому кресленні площина АВС є площиною рівня, а проекція 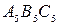 відповідає його натуральній величині.
відповідає його натуральній величині.
Для перетворення площини загального положення в площину рівня послідовно розв’язують третю та четверту задачі на одному комплексному кресленні (рис. 5.53). Треба створити таку нову ортогональну систему площин проекцій, в якій одна з цих площин була б паралельна трикутному відсіку. В системі  ,
, 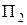 таку площину побудувати неможливо. Дійсно, площина, паралельна трикутнику, не буде перпендикулярною ні до
таку площину побудувати неможливо. Дійсно, площина, паралельна трикутнику, не буде перпендикулярною ні до  , ні до
, ні до 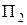 , тобто вона не утворює з площинами проекцій ортогональної системи. Звідси випливає необхідність виконання подвійної заміни площин проекцій. Спочатку площина
, тобто вона не утворює з площинами проекцій ортогональної системи. Звідси випливає необхідність виконання подвійної заміни площин проекцій. Спочатку площина 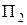 замінена площиною
замінена площиною 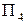 , а потім площина
, а потім площина  площиною
площиною 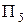 .
.
6. МЕТРИЧНІ ЗАДАЧІ
При розробці технічних креслень дуже часто доводиться розв’язувати метричні задачі, які пов’язані з вимірюванням різних параметрів геометричних образів.
Умовно ці задачі можна об’єднати у три групи:
1. Вимірювання довжин і відстаней:
2. Визначення дійсних величин плоских фігур і перерізів:
3. Вимірювання кутів.
Метричні задачі доцільно розв’язувати за допомогою розглянутих вище способів перетворення проекцій.
6.13. Визначення кута між прямою і площиною
 Кутом між прямою m і площиною T (рис. 6.16) називається гострий кут
Кутом між прямою m і площиною T (рис. 6.16) називається гострий кут 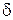 , утворений цією прямою з її проекцією на дану площину. Побудова проекцій кута
, утворений цією прямою з її проекцією на дану площину. Побудова проекцій кута 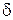 вимагає визначення двох точок K і L, перша із яких є точкою перетину даної прямої з площиною
вимагає визначення двох точок K і L, перша із яких є точкою перетину даної прямої з площиною 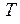 , а друга – основою перпендикуляра, опущеного із довільної точки А прямої на ту ж площину. Здобувши дві прямі, що перетинаються в точці К (прямі m і l), визначаємо дійсну величину кута між ними способом, розглянутим вище.
, а друга – основою перпендикуляра, опущеного із довільної точки А прямої на ту ж площину. Здобувши дві прямі, що перетинаються в точці К (прямі m і l), визначаємо дійсну величину кута між ними способом, розглянутим вище.
Подібний хід розв'язання задачі, хоча й є логічним, але він достатньо складний для виконання на комплексному кресленні. Цю задачу доцільно розв’язувати за допомогою так званого "додаткового" кута. Дійсно, з розгляду рис. 6.16 випливає, що трикутник ALK прямокутний. Тому сума кутів 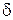 і
і 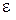 дорівнює
дорівнює 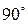 . Якщо будь-яким відомим нам способом визначити дійсну величину кута
. Якщо будь-яким відомим нам способом визначити дійсну величину кута 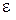 між прямою m і перпендикуляром n до площини Т, то додатковий до
між прямою m і перпендикуляром n до площини Т, то додатковий до 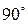 кут, який дорівнює
кут, який дорівнює 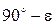 , буде шуканим кутом
, буде шуканим кутом 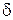 між прямою m та площиною Т.
між прямою m та площиною Т.
Розв'яжемо цю задачу на комплексному кресленні (рис. 6.17). Визначимо величину кута між прямою а і площиною  , яку задано двома паралельними прямими b i c. Для розв’язання цієї задачі застосуємо метод "додаткового" кута.
, яку задано двома паралельними прямими b i c. Для розв’язання цієї задачі застосуємо метод "додаткового" кута.
Із довільної точки К прямої а опускаємо перпендикуляр n на площину  , для чого в цій площині проводимо її горизонталь h і фронталь f. Далі обертанням навколо прямої рівня (наприклад, горизонталі
, для чого в цій площині проводимо її горизонталь h і фронталь f. Далі обертанням навколо прямої рівня (наприклад, горизонталі 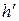 ) визначаємо натуральну величину кута
) визначаємо натуральну величину кута 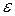 між заданою прямою а і перпендикуляром n до площини
між заданою прямою а і перпендикуляром n до площини  . Знаходимо нове положення
. Знаходимо нове положення 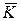 точки К і з’єднуємо його з нерухомими точками 1 і 2 на осі обертання
точки К і з’єднуємо його з нерухомими точками 1 і 2 на осі обертання 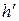 , отримуємо натуральну величину кута
, отримуємо натуральну величину кута 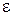 . Будуємо додатковий до
. Будуємо додатковий до 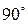 кут
кут 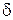 . Цей кут і буде кутом між прямою а і площиною
. Цей кут і буде кутом між прямою а і площиною  .
.
6.14. Визначення кута між площинами
Мірою кута між двома площинами є лінійний кут, утворений двома прямими, які є перерізами граней цього кута площиною, перпендикулярною до їх спільного ребра. Для знаходження лінійного кута необхідно виконати такі геометричні побудови (рис. 6.18):
1. Визначити у просторі пряму а, яка є лінією перетину двох заданих площин 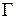 і
і 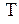 .
.
2. Провести нову площину  , перпендикулярну до прямої а.
, перпендикулярну до прямої а.
3. Побудувати лінії перетину k i l площини  з площинами
з площинами 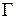 і
і 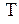 .
.
4.
Знайти величину кута 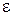 між прямими k i l, який визначає величину кута між площинами
між прямими k i l, який визначає величину кута між площинами 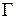 і
і 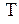 . Якщо цей кут перевищує
. Якщо цей кут перевищує 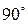 , то за міру кута між площинами беруть кут додатковий до
, то за міру кута між площинами беруть кут додатковий до 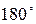 .
.
Розглянутий план розв’язання задачі передбачає виконання значної кількості геометричних побудов, які пов’язані з находженням лінії а перетину двох заданих площин, проведенням площини  , перпендикулярної до лінії перетину, подвійним розв’язанням задачі по визначенню ліній перетину площин, тобто знаходженню прямих k і l. Тільки після цього можна приступити до знаходження величини кута
, перпендикулярної до лінії перетину, подвійним розв’язанням задачі по визначенню ліній перетину площин, тобто знаходженню прямих k і l. Тільки після цього можна приступити до знаходження величини кута 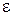 , який у загальному випадку утворюється прямими загального положення.
, який у загальному випадку утворюється прямими загального положення.
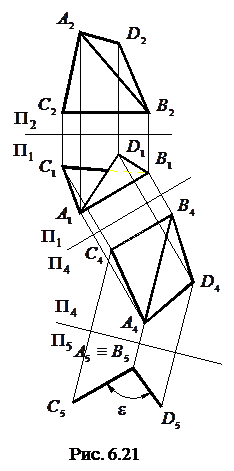
Подивимося, як можна спростити розв’язання цієї задачі. Доповнимо рис. 6.18 точкою К, яка належатиме площині  , і опустимо з цієї точки перпендикуляри m i n на площини
, і опустимо з цієї точки перпендикуляри m i n на площини  і
і  (рис. 6.19). Точки С і D перетину цих перпендикулярів з площинами сумісно з точками К і В є вершинами плоского чотирикутника КСВD, у якого кути при вершинах С і D прямі. Отже, між кутами
(рис. 6.19). Точки С і D перетину цих перпендикулярів з площинами сумісно з точками К і В є вершинами плоского чотирикутника КСВD, у якого кути при вершинах С і D прямі. Отже, між кутами  і
і 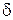 існує залежність
існує залежність 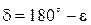 . З рис. 6.19 випливає, що замість кута
. З рис. 6.19 випливає, що замість кута 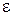 значно простіше знаходити кут
значно простіше знаходити кут 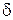 , додатковий до
, додатковий до 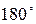 .Тобто й у цьому випадку доцільно застосовувати спосіб "додаткового" кута.
.Тобто й у цьому випадку доцільно застосовувати спосіб "додаткового" кута.
Приклад розв’язання подібної задачі подано на рис. 6.20, на якому площини задані головними своїми лініями. Для визначення кута між цими площинами із довільної точки К простору до них проведені два перпендикуляри n i  . Далі задача зводиться до визначення кута між двома прямими n i
. Далі задача зводиться до визначення кута між двома прямими n i  , що перетинаються. У нашому прикладі її розв’язано способом обертання навколо прямої рівня. Оскільки кут
, що перетинаються. У нашому прикладі її розв’язано способом обертання навколо прямої рівня. Оскільки кут 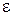 гострий, то він є мірою шуканого кута між цими площинами і, отже, немає потреби шукати додатковий до
гострий, то він є мірою шуканого кута між цими площинами і, отже, немає потреби шукати додатковий до 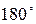 кут.
кут.
Визначення кута між двома площинами значно спрощується, якщо площини задані таким чином, що на комплексному кресленні присутня лінія їх перетину. Тобто дві площини явно утворюють двограний кут (рис. 6.21). У цьому випадку розв’язання задачі зводиться до перетворення лінії АВ, яка є прямою загального положення, у проекціювальну пряму, що можливе послідовним виконанням першої та другої основних задач. Обидві площини при цьому також займуть положення проекціювальних площин.
На рис. 6.21 задача розв’язана способом заміни площин проекцій. Після першої заміни відрізок АВ – спільне ребро двограного кута – зайняв положення прямої рівня. Це є результатом того, що нова вісь проекцій 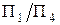 була розташована паралельно горизонтальній проекції
була розташована паралельно горизонтальній проекції 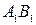 ребра.
ребра.
Після другої заміни площин проекцій, коли площина  була замінена площиною
була замінена площиною 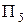 , відрізок АВ перетворився у проекціювальнну пряму. Нова вісь проекцій
, відрізок АВ перетворився у проекціювальнну пряму. Нова вісь проекцій 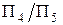 перпендикулярна до проекції
перпендикулярна до проекції 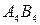 відрізка АВ. Кут
відрізка АВ. Кут  між проекціями-прямими площин є шуканим кутом між заданими площинами.
між проекціями-прямими площин є шуканим кутом між заданими площинами.
На завершення відзначимо, що розглянуті вище метричні задачі, більшість з яких доцільно розв’язувати із застосуванням способів перетворення комплексного креслення, дуже часто входять складовою частиною до різноманітних конструктивних задач, які на практиці доводиться розв'язувати при розробці тих чи інших технічних проектів. Тому оволодіння методами їх розв’язання має дуже важливе практичне значення.
КРИВІ ЛІНІЇ ТА ПОВЕРХНІ НА КОМПЛЕКСНОМУ КРЕСЛЕННІ
Кривою лінією називається неперервна сукупність послідовних положень точки, що рухається у просторі.
Криві лінії використовуються в різних галузях науки і техніки. Вони знаходять широке застосування при конструюванні поверхонь різних технічних форм; різних архітектурних деталей та конструкцій. Криві лінії – це обриси багатьох деталей машин та механізмів, траєкторії руху тіл. В нарисній геометрії криві лінії є твірними кінематичних поверхонь.
Способи утворення кривих ліній:
1. рухом точки у просторі,
2. перетином кривої поверхні площиною (у загальному випадку),
3. взаємним перетином двох поверхонь.
Класифікація кривих ліній.
1. За способом розташування у просторі – бувають плоскі та просторові криві.
Плоскі – це криві, всі точки яких належать одній площині, що називається площиною кривини кривої. До них відносяться коло, еліпс, парабола, гіпербола, лінії перетину кривих поверхонь тощо.
Просторові криві (або лінії подвійної кривини) – це криві, точки яких не належать одній площині. До них відносяться гвинтові лінії, лінії перетину двох кривих поверхонь.
- За способом утворення криві бувають закономірними та незакономірними.
Закономірні криві утворюються за визначеним законом. Вони можуть бути заданими аналітично (рівнянням) або графічно – за допомогою метрично визначених моделей.
Незакономірні криві задаються графічно, як відображення випадкового процесу або результатів експерименту (топологічна лінія, ватерлінія, батокс, шпангоут).
Порядок кривої лінії визначається степенем алгебраїчного рівняння, яке описує криву. З геометричної точки зору порядок плоскої алгебраїчної кривої визначається числом точок (дійсних та уявних) перетину її з прямою лінією. Порядок просторової кривої визначається числом точок перетину цієї лінії з площиною.
Криві можуть бути гладкими (радіус кривини плавно змінює своє значення), можуть мати точку перегину (таку, в якій радіус кривини має нескінченне значення), мати точку зламу (точка, в якій не можна провести дотичну, а радіус кривини не має ніякого значення), мати подвійні точки (або точки повертання кривої).
Пряма лінія відносно кривої може займати такі принципово різні положення (рис. 1.5): січна (t), дотична (t1), нормаль (n).
Січною називають таку пряму, яка має з кривою лінією не менше двох спільних точок. Дотична до кривої – це граничне положення січної, коли вона проходить через дві нескінченно близькі точки кривої. Нормаллю кривої у заданій точці називають таку пряму n, яка лежить у площині кривої і є перпендикулярною до дотичної прямої у цій точці.


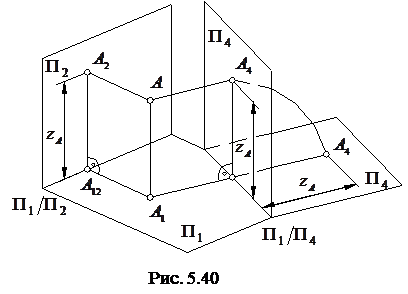 Подивимося, які зміни відбуваються з проекціями точки при переході від однієї системи площин проекцій до іншої. На рис. 5.40 показано точку А, що знаходиться в системі площин проекцій
Подивимося, які зміни відбуваються з проекціями точки при переході від однієї системи площин проекцій до іншої. На рис. 5.40 показано точку А, що знаходиться в системі площин проекцій  . Замінимо одну з цих площин, наприклад П2, іншою, також вертикальною площиною П4 і побудуємо проекцію точки А на цю площину. Оскільки горизонтальна площина проекцій П1 є спільною для "старої" та "нової" систем, то координата z точки А залишається незмінною. Отже, відстань від нової проекції
. Замінимо одну з цих площин, наприклад П2, іншою, також вертикальною площиною П4 і побудуємо проекцію точки А на цю площину. Оскільки горизонтальна площина проекцій П1 є спільною для "старої" та "нової" систем, то координата z точки А залишається незмінною. Отже, відстань від нової проекції  до нової осі
до нової осі  дорівнює відстані від проекції, що замінюється, до осі
дорівнює відстані від проекції, що замінюється, до осі  залишається тією ж самою, але координата у точки А тепер інша. Вона визначається відстанню від точки А до площини П4, яка на комплексному кресленні дорівнює відстані від проекції
залишається тією ж самою, але координата у точки А тепер інша. Вона визначається відстанню від точки А до площини П4, яка на комплексному кресленні дорівнює відстані від проекції  Для побудови комплексного креслення площина П4 обертанням навколо осі
Для побудови комплексного креслення площина П4 обертанням навколо осі 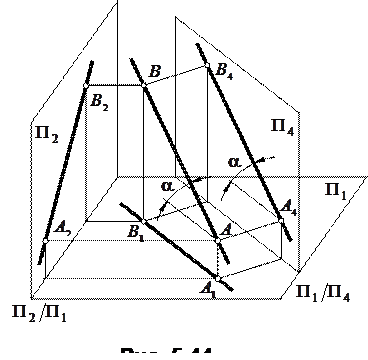 Розв’язання чотирьох основних задач способом заміни площин проекцій
Розв’язання чотирьох основних задач способом заміни площин проекцій /
/  задано відрізок АВ прямої загального положення (рис. 5.44). Для того, щоб у новій системі площин ця пряма зайняла положення прямої рівня, необхідно нову площину проекцій
задано відрізок АВ прямої загального положення (рис. 5.44). Для того, щоб у новій системі площин ця пряма зайняла положення прямої рівня, необхідно нову площину проекцій  розташувати паралельно відрізку АВ і перпендикулярно до площини проекцій
розташувати паралельно відрізку АВ і перпендикулярно до площини проекцій 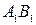 відрізка АВ. Спроекціювавши АВ на площину
відрізка АВ. Спроекціювавши АВ на площину 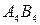 . Для здобуття нового плоского комплексного креслення площину
. Для здобуття нового плоского комплексного креслення площину 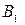 горизонтальної проекції відрізка до нових проекцій, перпендикулярно до нової осі.
горизонтальної проекції відрізка до нових проекцій, перпендикулярно до нової осі.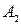 і
і 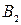 від осі
від осі 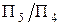 перпендикулярно до проекції
перпендикулярно до проекції 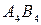 , що випливає з умови задачі, пов’язаної з перетворенням прямої рівня у пряму проекціювальну.
, що випливає з умови задачі, пов’язаної з перетворенням прямої рівня у пряму проекціювальну.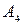 і
і 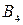 , що переходять із старого у нове комплексне креслення, проводимо нові лінії сполучення, перпендикулярно до нової осі
, що переходять із старого у нове комплексне креслення, проводимо нові лінії сполучення, перпендикулярно до нової осі 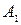 і
і 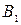 точок до старої осі
точок до старої осі 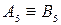 відрізка АВ.
відрізка АВ.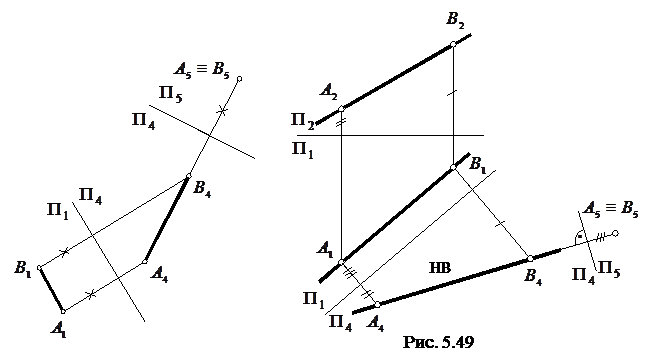
 Розташувавши
Розташувавши  , забезпечуємо виконання одразу двох умов: нова площина
, забезпечуємо виконання одразу двох умов: нова площина  проводять під прямим кутом до
проводять під прямим кутом до  . Провівши через горизонтальні проекції вершин трикутника лінії сполучення, перпендикулярні до нової осі, відкладаємо на них від осі
. Провівши через горизонтальні проекції вершин трикутника лінії сполучення, перпендикулярні до нової осі, відкладаємо на них від осі  ,
,  ,
, 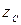 . Далі будується нова проекція
. Далі будується нова проекція 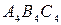 трикутника АВС, яка є прямою лінією. Додамо також, що на площину
трикутника АВС, яка є прямою лінією. Додамо також, що на площину  , утворений трикутним відсіком з площиною проекцій
, утворений трикутним відсіком з площиною проекцій 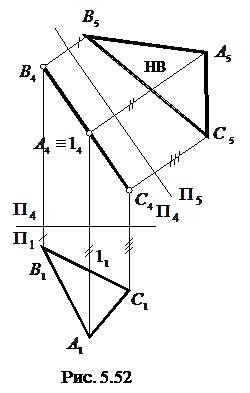 Нагадаємо, що для перетворення проекціювальної площини у площину рівня необхідно ввести нову площину проекції
Нагадаємо, що для перетворення проекціювальної площини у площину рівня необхідно ввести нову площину проекції 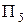 , паралельну площині трикутника. Вісь проекцій
, паралельну площині трикутника. Вісь проекцій 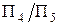 має бути паралельною "виродженій" проекції три-кутника, яка є результатом розв’язання третьої задачі.
має бути паралельною "виродженій" проекції три-кутника, яка є результатом розв’язання третьої задачі.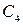 проводять нові лінії сполучення, перпендикулярні до нової осі
проводять нові лінії сполучення, перпендикулярні до нової осі  ,
, 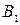 ,
, 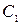 від старої осі
від старої осі 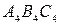 відсіку та його нової, додаткової проекції
відсіку та його нової, додаткової проекції 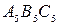 . На цьому кресленні площина АВС є площиною рівня, а проекція
. На цьому кресленні площина АВС є площиною рівня, а проекція 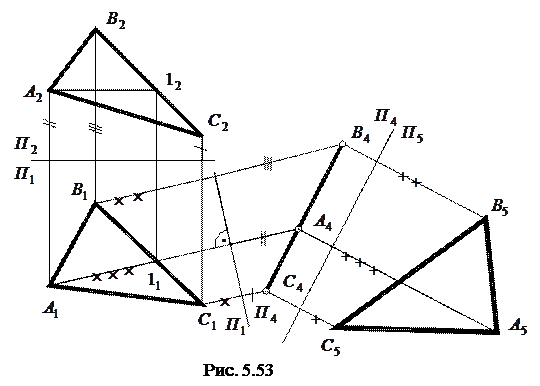
 , а потім площина
, а потім площина  Кутом між прямою m і площиною T (рис. 6.16) називається гострий кут
Кутом між прямою m і площиною T (рис. 6.16) називається гострий кут  , утворений цією прямою з її проекцією на дану площину. Побудова проекцій кута
, утворений цією прямою з її проекцією на дану площину. Побудова проекцій кута  , а друга – основою перпендикуляра, опущеного із довільної точки А прямої на ту ж площину. Здобувши дві прямі, що перетинаються в точці К (прямі m і l), визначаємо дійсну величину кута між ними способом, розглянутим вище.
, а друга – основою перпендикуляра, опущеного із довільної точки А прямої на ту ж площину. Здобувши дві прямі, що перетинаються в точці К (прямі m і l), визначаємо дійсну величину кута між ними способом, розглянутим вище.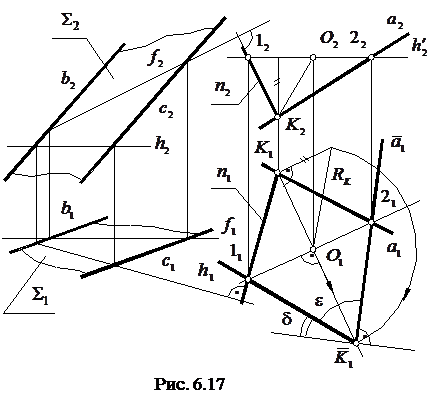
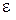 дорівнює
дорівнює 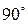 . Якщо будь-яким відомим нам способом визначити дійсну величину кута
. Якщо будь-яким відомим нам способом визначити дійсну величину кута 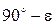 , буде шуканим кутом
, буде шуканим кутом  , яку задано двома паралельними прямими b i c. Для розв’язання цієї задачі застосуємо метод "додаткового" кута.
, яку задано двома паралельними прямими b i c. Для розв’язання цієї задачі застосуємо метод "додаткового" кута.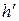 ) визначаємо натуральну величину кута
) визначаємо натуральну величину кута 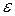 між заданою прямою а і перпендикуляром n до площини
між заданою прямою а і перпендикуляром n до площини 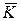 точки К і з’єднуємо його з нерухомими точками 1 і 2 на осі обертання
точки К і з’єднуємо його з нерухомими точками 1 і 2 на осі обертання 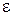 . Будуємо додатковий до
. Будуємо додатковий до 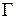 і
і 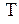 .
. , перпендикулярну до прямої а.
, перпендикулярну до прямої а.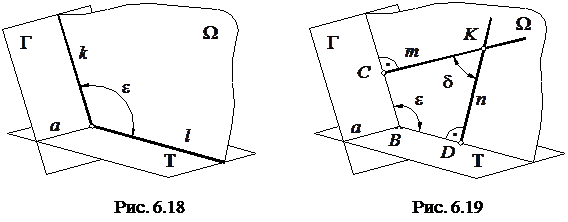
 .
.
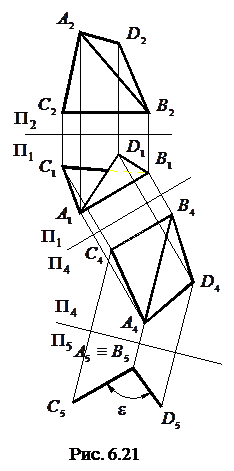
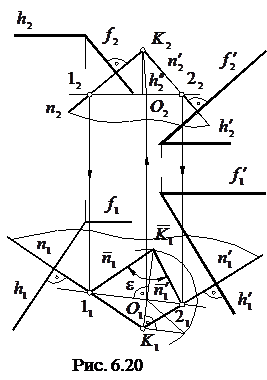
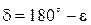 . З рис. 6.19 випливає, що замість кута
. З рис. 6.19 випливає, що замість кута  . Далі задача зводиться до визначення кута між двома прямими n i
. Далі задача зводиться до визначення кута між двома прямими n i  перпендикулярна до проекції
перпендикулярна до проекції