З графіка на рис. 10 видно, що при деякому значенні норми дисконтування (яке знаходиться між 9% і 10%) чистий приведений дохід звертається в нуль. Це значення норми дисконтування і називається внутрішньою нормою прибутковості (internal rate of return, IRR). Таким чином, внутрішня норма прибутковості інвестиційного проекту є розрахунковою ставкою відсотків, при якій чистий приведений дохід, відповідний цьому проекту, рівний нулю. Економічне значення цього показника можна пояснити таким чином. Як альтернатива вкладенням фінансових коштів в інвестиційний проект розглядається приміщення тих же засобів (так само розподілених за часом вкладення) під деякий банківський відсоток. Розподілені в часі доходи, одержувані від реалізації інвестиційного проекту, також поміщаються на депозитний рахунок в банку під той же відсоток.
При ставці позикового відсотка, рівній внутрішній нормі прибутковості, інвестування фінансових коштів в проект дасть у результаті той же сумарний дохід, що і приміщення їх в банк на депозитний рахунок. Таким чином, при цій ставці позикового відсотка обидві альтернативи приміщення фінансових коштів економічно еквівалентні. Якщо реальна ставка позикового відсотка менше внутрішньої норми прибутковості проекту, то інвестування засобів в нього вигідне, і навпаки. Отже, IRR є граничною ставкою позикового відсотка, розподіляючи ефективні і неефективні інвестиційні проекти.
Із сказаного виходить, що рівень IRR повністю визначається внутрішніми даними, що характеризують інвестиційний проект. Ніякі припущення про використовування чистого доходу за межами проекту не розглядаються.
За рубежем розрахунок внутрішньої норми прибутковості часто застосовується як перший крок при фінансовому аналізі інвестиційного проекту. Для подальшого аналізу відбирають ті інвестиційні проекти, які мають IRR не нижче за деякі порогові значення (звично 15-20 % річних).
Методика визначення внутрішньої норми прибутковості залежить від конкретних особливостей розподілу доходів від інвестицій і самих інвестицій. У загальному випадку, коли інвестиції і віддача від них задаються у вигляді потоку платежів, IRR визначається як рішення наступного рівняння щодо невідомої величини d*:
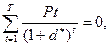 (5.3)
(5.3)
де: d* = IRR - внутрішня норма прибутковості, відповідна потоку платежів Pt.
Воно може бути одержане з формули (5.2), якщо її ліву частину прирівняти до нуля.
Рівняння (5.3) еквівалентне рівнянню алгебри ступеня Т і звичайно розв'язується методом ітерацій. Існують численні програми для ПЕВМ, вирішальні подібні рівняння.
У розглянутому вище прикладі IRR рівна 9,6%. Затягування термінів початку випуску продукції на 2 роки після закінчення будівництва знижує внутрішню норму прибутковості до 7%.
Ясно, що величина IRR залежить не тільки від співвідношення сумарних капітальних вкладень і доходів від реалізації проекту, але і від їх розподілу в часі. Чим більше розтягнутий в часі процес отримання доходів в результаті зроблених вкладень, тим нижче значення внутрішньої норми прибутковості. Графік, представлений на рис. 10 один раз перетинає нульову відмітку, що типове для більшості інвестиційних проектів. В цьому випадку рівняння (5.3) має єдине позитивне коріння, відповідне єдиному значенню IRR. Проте на практиці можуть зустрічатися складніші випадки, коли це рівняння має декілька позитивного коріння. Це може, наприклад, відбутися, коли вже після первинних інвестицій у виробництво виникає необхідність крупної модернізації або заміни устаткування на діючому виробництві. У останньому випадку слід керуватися як найменшим значенням з одержаних рішень.


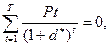 (5.3)
(5.3)