Ланцюжок 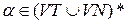 , для якої
, для якої 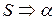 називається сентенціальною формою в граматиці G=(VT, VN, P, S).
називається сентенціальною формою в граматиці G=(VT, VN, P, S).
Висновок ланцюжка 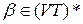 з
з 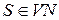 у КС-граматиці G=(VT, VN, P, S), називається правим (правобічним), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого правого нетермінала.
у КС-граматиці G=(VT, VN, P, S), називається правим (правобічним), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого правого нетермінала.
У граматиці, для одного і того самого ланцюжка може бути кілька висновків, еквівалентних у тому розумінні, що в них у тих самих місцях застосовуються ті самі правила висновку, але в різному порядку.
Наприклад: для ланцюжка a+b+c у граматиці
G=({a,b},{S,T}, {S T½T+S; T
T½T+S; T a½b},S) можна побудувати висновки:
a½b},S) можна побудувати висновки:
1) S T+S
T+S T+T+S
T+T+S T+T+T
T+T+T a+T+T
a+T+T a+b+T
a+b+T a+b+a
a+b+a
2) S T+S
T+S a+S
a+S a+T+S
a+T+S a+b+S
a+b+S a+b+T
a+b+T a+b+a
a+b+a
3) S T+S
T+S T+T+S
T+T+S T+T+T
T+T+T T+T+a
T+T+a T+b+a
T+b+a a+b+a
a+b+a
Тут 2 – лівосторонній висновок, 3 – правобічний, а 1 не є ні лівостороннім, ні правобічним, але всі ці висновки є еквівалентними в зазначеному вищі розумінні.
Для КВ-граматик можна ввести зручне графічне представлення висновку, назване деревом висновку, причому для всіх еквівалентних висновків дерева висновки збігаються.
Дерево називається деревом висновку (чи деревом розбору) у КВ-граматиці G=(VT, VN, P, S), якщо виконані наступні умови:
1) кожна вершина дерева позначена символом з множини  , при цьому корінь дерева позначений символом S; гілки – символами з
, при цьому корінь дерева позначений символом S; гілки – символами з 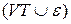 ;
;
2) якщо вершина дерева позначена символом 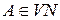 , а її безпосередні нащадки – символами a1, … an, де кожне
, а її безпосередні нащадки – символами a1, … an, де кожне 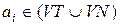 , то
, то 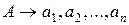 – правило висновку у цій граматиці;
– правило висновку у цій граматиці;
3) якщо вершина дерева позначена символом 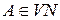 , а її єдиний безпосередній нащадок позначений символом
, а її єдиний безпосередній нащадок позначений символом 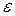 , то
, то 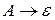 – правило у цій граматиці.
– правило у цій граматиці.
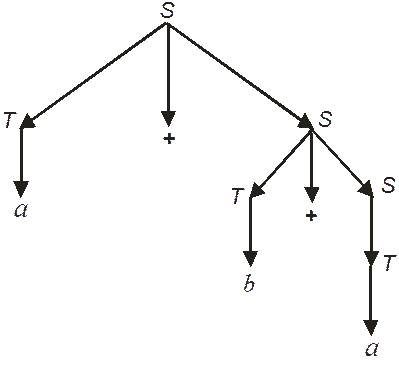
Приклад дерева висновку для ланцюжка a+b+a у граматиці G показано на рис.3.1.


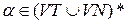 , для якої
, для якої 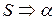 називається сентенціальною формою в граматиці G=(VT, VN, P, S).
називається сентенціальною формою в граматиці G=(VT, VN, P, S).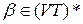 з
з 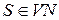 у КС-граматиці G=(VT, VN, P, S), називається правим (правобічним), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого правого нетермінала.
у КС-граматиці G=(VT, VN, P, S), називається правим (правобічним), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого правого нетермінала. T½T+S; T
T½T+S; T , при цьому корінь дерева позначений символом S; гілки – символами з
, при цьому корінь дерева позначений символом S; гілки – символами з 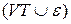 ;
;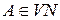 , а її безпосередні нащадки – символами a1, … an, де кожне
, а її безпосередні нащадки – символами a1, … an, де кожне 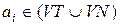 , то
, то 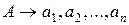 – правило висновку у цій граматиці;
– правило висновку у цій граматиці;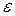 , то
, то 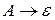 – правило у цій граматиці.
– правило у цій граматиці.