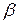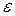Рис.3.1. Дерево висновку для ланцюжка a+b+a у граматиці G
КВ-граматика G називається неоднозначною, якщо існує хоча б один ланцюжок 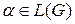 , для якого може бути побудовано два чи більше різних дерева висновку.
, для якого може бути побудовано два чи більше різних дерева висновку.
Це твердження еквівалентне тому, що ланцюжок 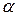 має два чи більше різних лівосторонніх чи правобічних висновків.
має два чи більше різних лівосторонніх чи правобічних висновків.
У протилежному випадку граматика називається однозначною.
Мова, породжена граматикою, називається неоднозначною, якщо вона не може бути породжена ніякою однозначною граматикою.
Приклад неоднозначної граматики:
G=({if, then, else, a, b}, {S}, P,S), де P={S if b then S else S½if b then S½a}.
if b then S else S½if b then S½a}.
У цій граматиці для ланцюжка if b then if b then a else a можна побудувати два дерева висновку. Однак це не означає, що мова L(G) обов‘язково неоднозначна.
Визначена нами неоднозначність – це властивість граматики, а не мови, тобто для деяких неоднозначних граматик існують еквівалентні їм однозначні граматики. Якщо граматика використовується для визначення мови програмування, то вона повинна бути однозначною. У наведеному вище прикладі різні дерева висновку припускають відповідність else різним then, і якщо підправити граматику G, то неоднозначність буде усунута:
S if b then S½if b then S| else S½a
if b then S½if b then S| else S½a
S| b then S| else S| | a
b then S| else S| | a
Проблема, чи породжує дана КС-граматика однозначну мову (тобто чи існує еквівалентна їй однозначна граматика), є алгоритмічно нерозв‘язуваною.
Однак можна вказати деякі види правил висновку, що приводять до неоднозначності.
1. A AA |
AA |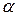
2. A A
A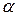 A½
A½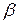
3. A
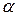 A |A
A |A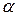 |
|
4. A
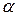 A½
A½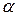 A
A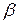 A½
A½
Приклад неоднозначної КС мови:
L = {a ibj ck | i=j чи j=k}.
Інтуїтивно це пояснюється тим, що ланцюжки з i=j повинні породжуватись групою правил висновку, відмінних від правил, що породжують ланцюжки з j=k. Але тоді, певні з ланцюжків з i=j=k будуть породжуватись обома групами правил, та відповідно будуть мати по два різних дерева висновку.
Одна з граматик, що породжує L така:
S AB | DC
AB | DC
A aA |
aA | 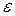
B bBc½
bBc½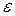
C cC½
cC½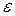
D aDb½
aDb½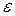
Очевидно, що вона неоднозначна.
Дерево виведення можна будувати знизу вверх, чи з гори вниз.
При формуванні дерева згори вниз, дерево формується від кореня до гілок. На кожному крокові для вершини, позначеної нетермінальним символом, намагаються знайти таке правило висновку, щоб наявні в ньому термінальні символи «проектувались на символи» вихідного ланцюжка.
Метод «знизу до гори» полягає у тому, що вихідний ланцюжок намагаються «згорнути» до початкового символу S; на кожному крокові шукають ланцюжок який співпадає з правою частиною будь-якого правила висновку; якщо такий підланцюжок знаходиться, то вона замінюється нетерміналом з лівої частини правила.
Якщо граматика однозначна, то при будь-якому способі побудови, буде отримане одне й те саме дерево.
В певних випадках КВ-граматика може містити недосяжні та марні символи, котрі не беруть участь у породженні ланцюжків мови і тому можуть бути видаленими з граматики.


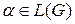 , для якого може бути побудовано два чи більше різних дерева висновку.
, для якого може бути побудовано два чи більше різних дерева висновку.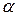 має два чи більше різних лівосторонніх чи правобічних висновків.
має два чи більше різних лівосторонніх чи правобічних висновків. if b then S else S½if b then S½a}.
if b then S else S½if b then S½a}.